Bài 2.19 trang 38 sgk toán 7 tập 1 Kết nối tri thức
Câu hỏi
Cho bốn phân số:\(\frac{17}{80}=0,2125 ; \frac{611}{125}=4,888 ; \frac{133}{91}=1,(461538) ; \frac{9}{8}=1,125 ; \frac{17}{80} ; \frac{611}{125} ; \frac{133}{91} ; \frac{9}{8}\)
a) Phân số nào trong những phân số trên không viết được dưới dạng số thập phân hữu hạn?
b) Cho biết ,\(\sqrt{2}=1,414213562 \ldots\) hãy so sánh phân số tìm được trong câu a) với \(\sqrt{2}\)
Bài giải
\(\frac{17}{80}=0,2125 ; \frac{611}{125}=4,888 ; \frac{133}{91}=1,(461538) ; \frac{9}{8}=1,125\)
Như vậy, trong những phân số trên, phân số không viết được dưới dạng số thập phân hữu hạn là: \(\frac{133}{91}\)
b) Ta có: \(\frac{133}{91}=1,(461538)=1,461538461538 \ldots \ldots\)
Quan sát chữ số thập phân thứ 2 của 2 số, vì 1 < 6 nên \(1,414213562 \cdots<1,461538461538\)
Vậy \(\frac{133}{91}>\sqrt{2}\)
Bài 2.20 trang 38 sgk toán 7 tập 1 Kết nối tri thức
Câu hỏi
a) Viết các phân số sau dưới dạng số thập phân vô hạn tuần hoàn (dùng dấu ngoặc để chỉ rõ chu kì): \(\frac{1}{9} ; \frac{1}{99}\)m
Em có nhận xét gì về kết quả nhận được?
b) Em hãy dự đoán dạng thập phân của \(\frac{1}{{999}}.\) ?
Bài giải
a) Thực hiện đặt phép chia ta có: \(\frac{1}{9} = 0,\left( 1 \right);\,\,\frac{1}{{99}} = 0,\left( {01} \right).\)
Nhận xét: Trong 2 phân số trên, số chữ số 0 trong chu kì bằng số chữ số 9 của mẫu số trừ đi 1, sau đó đến một chữ số 1.
b) 999 là số có 3 chữ số nên có 2 chữ số 0 trong chu kì dạng thập phân của \(\frac{1}{{999}}\), sau đó đến một chữ số 1.
Dự đoán dạng thập phân của \(\frac{1}{{999}}\) là 0,(001).
Bài 2.21 trang 38 sgk toán 7 tập 1 Kết nối tri thức
Câu hỏi
Viết \(\frac{5}{9}\) và \(\frac{5}{{99}}\) dưới dạng số thập phân vô hạn tuần hoàn.
Bài giải
Sử dụng kết quả Bài 2.20, thu được: \(\frac{5}{9} = 0,\left( 5 \right);\,\frac{5}{{99}} = 0,\left( {05} \right).\)
Bài 2.22 trang 38 sgk toán 7 tập 1 Kết nối tri thức
Câu hỏi
Nam vẽ một phần trục số trên vở ô li và đánh dấu ba điểm A, B, C như sau:
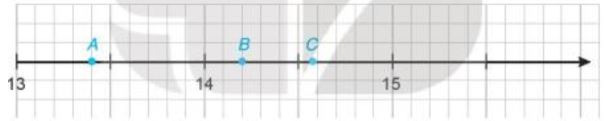
a) Hãy cho biết hai điểm A, B biểu diễn những số thập phân nào?
b) Làm tròn số thập phân được biểu diễn bởi điểm C với độ chính xác 0,05.
Bài giải
Trong hình trên, đoạn thẳng đơn vị được chia làm 2 phần bằng nhau, mỗi đoạn bằng \(\frac{1}{2}\) đoạn ban đầu bằng 0,5.
Chia đoạn có độ dài 0,5 thành 5 phần bằng nhau, mỗi đoạn bằng \(\frac{{0,5}}{5} = 0,1.\)
a) Điểm A cách điểm 13 một khoảng bằng 4 đoạn 0,1 nên điểm A biểu diễn số
13 + 4.0,1 = 13,4.
Điểm B cách điểm 14 một khoảng bằng 2 đoạn 0,1 nên điểm B biểu diễn số 14 + 2.0,1 = 14,2.
b) Làm tròn số thập phân được biểu diễn bởi điểm C với độ chính xác 0,05 ta thấy điểm C cách điểm 14 một khoảng bằng 6 đoạn 0,1 nên điểm C biểu diễn số 14 + 6.0,1 = 14,6.
Bài 2.23 trang 38 sgk toán 7 tập 1 Kết nối tri thức
Câu hỏi
Thay dấu “?” bằng chữ số thích hợp.
a) \(- 7,02 < - 7,\,?\,\left( 1 \right);\)
b) \( - 15,3 \,?\,021 < - 15,3819.\)
Bài giải
a) Ta có hai số thập phân có cùng phần nguyên bằng –7.
Mà 2 > 1 nên để −7,02<−7,?1 thì số cần điền là 0.
Khi đó −7,02<−7,01.
Vậy ? = 0.
b) Ta có hai số thập phân có cùng phần nguyên bằng –15.
Mà 3 = 3, 0 < 8 nên để −15,3?021<−15,3819 thì số cần điền là 9.
Do đó −15,39021<−15,3819.
Vậy ? = 9.
Bài 2.24 trang 38 sgk toán 7 tập 1 Kết nối tri thức
Câu hỏi
So sánh:
a) 12,26 và 12,(24);
b) 31,3(5) và 29,9(8).
Bài giải
a) Làm tròn kết quả với độ chính xác 0,005 được \(12,\left( {24} \right) = 12,242424... \approx 12,24.\)
Mà 12,26 > 12,24 nên 12,26 > 12,(24).
b) Vì 31 > 29 nên 31,3(5) > 29,9(8).
Vậy 31,3(5) > 29,9(8).
Bài 2.25 trang 38 sgk toán 7 tập 1 Kết nối tri thức
Câu hỏi
Tính:
a) \(\sqrt 1 ;\)
b) \(\sqrt {1 + 2 + 1} ;\)
c) \(\sqrt {1 + 2 + 3 + 2 + 1} .\)
Bài giải
a) Có 12 = 1 và 1 > 0 nên \(\sqrt 1 = 1.\)
b) Do 1 + 2 + 1 = 4 nên \(\sqrt {1 + 2 + 1} = \sqrt 4 .\)
Có 22 = 4 và 2 > 0 nên \(\sqrt 4 = 2.\)
Do đó \(\sqrt {1 + 2 + 1} = 2.\)
c) Do 1 + 2 + 3 + 2 + 1 = 9 nên \(\sqrt {1 + 2 + 3 + 2 + 1} = \sqrt 9 .\)
Có 32 = 9 và 3 > 0 nên \(\sqrt 9 = 3.\)
Do đó \(\sqrt {1 + 2 + 3 + 2 + 1} = 3.\)
Bài 2.26 trang 38 sgk toán 7 tập 1 Kết nối tri thức
Câu hỏi
Tính:
a) \({\left( {\sqrt 3 } \right)^2};\)
b) \({\left( {\sqrt {21} } \right)^2}.\)
Bài giải
Theo định nghĩa căn bậc hai số học có:
a) \({\left( {\sqrt 3 } \right)^2} = 3.\)
b) \({\left( {\sqrt {21} } \right)^2} = 21.\)
Bài tiếp theo: Trang 39 SGK Toán 7 tập 1 Kết nối tri thức
Xem thêm:
- Trang 28 SGK Toán 7 tập 1 Kết nối tri thức
- Trang 32 SGK Toán 7 tập 1 Kết nối tri thức
- Trang 36 SGK Toán 7 tập 1 Kết nối tri thức
Trên đây là chi tiết hướng dẫn Giải bài tập Trang 38 SGK Toán 7 tập 1 Kết nối tri thức được Đọc Tài Liệu biên soạn với mong muốn hỗ trợ các em học sinh học tốt hơn môn Toán lớp 7
Hướng dẫn giải Toán 7 Kết nối tri thức bởi Đọc Tài Liệu