Cùng Đọc tài liệu thử sức với đề thi thử vào lớp 10 môn toán năm học 2022 - 2023 của trường THPT Hoằng Hóa - Thanh Hóa vừa ra em nhé:
Đề thi thử vào 10 môn Toán - Hoằng Hóa 2022
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO - HUYỆN HOẰNG HÓA
ĐỀ THI THỬ VÀO LỚP 10 - THPT
NĂM HỌC: 2022 - 2023
Môn thi: Toán 120 phút (không kể thời gian giao đề)
Thời gian: 120 phút (không kể thời gian giao đề)
Câu 1. (2,0 điểm)
Cho biểu thức:
\(P = \dfrac{\sqrt{x}+1}{\sqrt{x}-2} + \dfrac{2\sqrt{x}}{\sqrt{x}+2} - \dfrac{2 + 5\sqrt{x}}{x - 4}\)
với x ≥ 0, x ≠ 4.
1. Rút gọn biểu thức P.
2. Tìm các giá trị của x để P = 3/2.
Câu 2. (2,0 điểm)
1. Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d) có phương trình: y = (2m - 1)x + m (m là tham số). Tìm m để đường thẳng (d) đi qua điểm P(1; 2).
2. Giải hệ phương trình:
\(\left\{ \matrix{ 3x - 2y=5 \hfill \cr 2x+2y=7 \hfill \cr} \right.\)
Câu 3. (2,0 điểm)
1. Giải phương trình: x² - 4x +3= 0.
2. Cho phương trình: x² – 4x + m – 1 = 0 (m là tham số). Tìm m để phương trình có hai nghiệm phân biệt thỏa mãn điều kiện: x₁(x₁+2)+x₂(x₂ + 2) = 20.
Câu 4. (3,0 điểm) Cho đường tròn (O; R) và điểm M cố định nằm ngoài (O; R). Từ M kẻ các tiếp tuyến MA, MB tới (O; R) (A, B là các tiếp điểm). Đường thẳng (d) bất kỳ qua M và cắt (O; R) tại hai điểm phân biệt C, D (C nằm giữa M và D). Gọi N là giao điểm của AB và CD.
a) Chứng minh rằng tứ giác OAMB nội tiếp.
b) Chứng minh rằng △ANC và △DNB đồng dạng, △AMC và DMA đồng dạng.
c) Chứng minh rằng: \(\dfrac{{MC}}{{MD}} = \dfrac{{NC}}{{ND}}.\)
d) Xác định vị trí của đường thẳng (d) để \(\dfrac{1}{{MD}} + \dfrac{1}{{ND}}\) đạt giá trị nhỏ nhất.
Câu 5. (1,0 điểm)
Cho các số thực dương a, b, c thỏa mãn: a + b + c = 1. Chứng minh rằng:
\(\dfrac{a^2}{a+b}+\dfrac{b^2}{b+c} + \dfrac{c^2}{c+a} ≥ \dfrac{1}{2}\)
- Hết -
Hướng dẫn giải bài hình - đề thi thử vào 10 môn toán Thanh Hóa 2022 - 2023
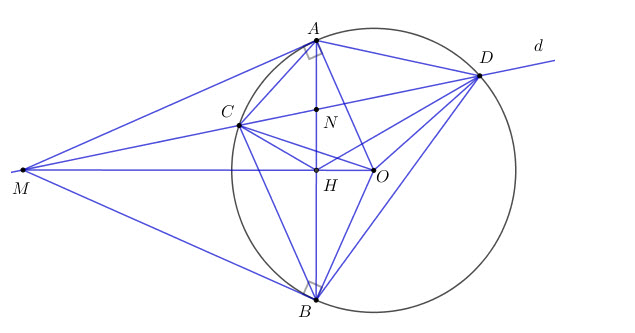
a) Vì MA,MB là hai tiếp tuyến của \(\left( O \right) \Rightarrow \widehat {MAO} = \widehat {MBO} = {90^0}\).
Xét tứ giác \(\widehat {MAO} + \widehat {OBM} = {90^0} + {90^0} = {180^0}\) => MAOB là tứ giác nội tiếp (dhnb).
b) Chứng minh rằng △ANC và △DNB đồng dạng, △AMC và △DMA đồng dạng.
Xét △ANC và △DNB ta có:
\(\widehat {CAN} = \widehat {NDB}\) (hai góc nội tiếp cùng chắn cung CB)
\(\widehat {ANC} = \widehat {DNB}\)
(hai góc đối đỉnh).\( \Rightarrow \Delta ANC \sim \Delta DNB\;\left( {g - g} \right)\;\;\;\;\left( {dpcm} \right).\)
Xét △AMC và △DMA ta có:
\(\widehat {AMD} \)chung
\(\widehat {MAC} = \widehat {MDA} \)(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung AC).
\( \Rightarrow \Delta MAC \sim \Delta MDA\;\;\left( {g - g} \right)\;\;\;\left( {dpcm} \right).\)
c) Chứng minh rằng: \(\dfrac{{MC}}{{MD}} = \dfrac{{NC}}{{ND}}.\)
Ta có: \(\Delta MAC \sim \Delta MDA\;\;\left( {cmt} \right) \)
\(\Rightarrow \dfrac{{MA}}{{MD}} = \dfrac{{MC}}{{MA}} \Leftrightarrow M{A^2} = MC.MD.\)
Gọi H là giao điểm của AB và MO \(\Rightarrow AB \bot MO = \left\{ H \right\}\). (tính chất hai tiếp tuyến cắt nhau)
Xét tam giác MAO vuông tại A và có đường cao AH có:
\(M{A^2} = MH.MO\). (hệ thức lượng trong tam giác vuông)
\(\begin{array}{l} \Rightarrow MC.MD = MH.MO\;\left( { = M{A^2}} \right).\\ \Rightarrow \dfrac{{MC}}{{MO}} = \dfrac{{MH}}{{MO}}.\end{array}\)
Xét △MCH và △MOD ta có:
\(\begin{array}{l}\dfrac{{MC}}{{MH}} = \dfrac{{MO}}{{MD}}\;\;\left( {cmt} \right)\\\widehat {OMD}\;\;chung\\ \Rightarrow \Delta MCH \sim \Delta MOD\;\;\left( {g - g} \right).\end{array}\)
\( \Rightarrow \widehat {MHC} = \widehat {MDO}\) (hai góc tương ứng).
Xét tứ giác CHOD ta có:
\(\widehat {MHC} = \widehat {CDO}\;\;\left( {cmt} \right)\)
=> CHOD là tứ giác nội tiếp. (góc ngoại tại một đỉnh bằng góc trong tại đỉnh đối diện)
\( \Rightarrow \widehat {DHO} = \widehat {DCO}\) (hai góc nội tiếp cùng chắn cung DO)
Lại có: \(\widehat {ODC} = \widehat {OCD}\) (△ COD cân tại O)
\( \Rightarrow \widehat {DHO} = \widehat {CHM}\left( { = \widehat {CDO}} \right).\)
Mà \(HM \bot HN\;\;\left( {cmt} \right)\)
\( \Rightarrow \widehat {NHC} = \widehat {NHD}\;\left( { = {{90}^0} - \widehat {CHM}} \right)\)
=> NH là tia phân giác trong của \(\widehat {CHD}\) và HM là tia phân giác ngoài của \(\widehat {CHD}\).
\( \Rightarrow \dfrac{{MC}}{{MD}} = \dfrac{{NC}}{{ND}}\left( { = \dfrac{{HC}}{{HD}}} \right).\;\;\left( {dpcm} \right)\)
d) Xác định vị trí của đường thẳng (d) để \(\dfrac{1}{{MD}} + \dfrac{1}{{ND}}\)đạt giá trị nhỏ nhất.
Xét:
\(\begin{array}{l} DC\left( {\dfrac{1}{{MD}} + \dfrac{1}{{ND}}} \right) = \dfrac{{CD}}{{MD}} + \dfrac{{CD}}{{ND}} \\= \dfrac{{MD - CM}}{{MD}} + \dfrac{{CN + ND}}{{ND}}\\ = 1 - \dfrac{{CM}}{{MD}} + 1 + \dfrac{{CN}}{{ND}} = 2 + \dfrac{{CN}}{{DN}} - \dfrac{{MC}}{{MD}} = 2.\;\;\;\left( {do\;\;\dfrac{{MC}}{{MD}} = \dfrac{{NC}}{{ND}}} \right)\\ \Rightarrow \dfrac{1}{{MD}} + \dfrac{1}{{ND}} = \dfrac{2}{{CD}}.\end{array}\)
Vì CD là dây cung
\(\Rightarrow CD \le 2R \Rightarrow \dfrac{2}{{CD}} \ge \dfrac{2}{{2R}} \Leftrightarrow \dfrac{2}{{CD}} \ge \dfrac{1}{R}.\)
\( \Rightarrow \dfrac{1}{{MD}} + \dfrac{1}{{ND}} \ge \dfrac{1}{R}.\)
Dấu “=” xảy ra ⇔ CD = 2R hay đường thẳng d đi qua O.
Vậy để \(\dfrac{1}{{MD}} + \dfrac{1}{{ND}}\) đạt giá trị nhỏ nhất thì đường thẳng d đi qua O.
-/-
Trên đây là hướng dẫn giải chi tiết đề thi thử vào 10 2022 môn toán của trường THPT Hoằng Hóa, mong rằng đây sẽ là tài liệu hữu ích giúp các em ôn tập. Đừng quên còn rất nhiều tài liêu đề thi thử vào 10 môn toán khác của các tỉnh thành trên cả nước nhé.
