Cùng Đọc tài liệu thử sức với đề thi thử vào lớp 10 môn toán năm học 2022 - 2023 lần thử đầu tiên của trường Lương Thế Vinh vừa ra em nhé:
Đề thi thử môn toán 2022 lần 1 Lương Thế Vinh
|
TRƯỜNG THCS & THPT LƯƠNG THẾ VINH |
ĐỀ THI THỬ VÀO 10 - LẦN 1 Năm học: 2022 – 2023 MÔN: TOÁN Thời gian làm bài: 120 phút |
Bài 1: (3 điểm)
Cho các biểu thức:\(A=\dfrac{3 \sqrt{x}-1}{\sqrt{x}+1}\) và \(B=\dfrac{2 \sqrt{x}}{\sqrt{x}+2}+\dfrac{3}{\sqrt{x}-2}+\dfrac{x+8}{4-x}\)
với x ≥ 0; x ≠ 4
a. Tính giá trị của biểu thức A khi x = 9
b. Rút gọn biểu thức B
c. Đặt P = A. B. Tìm các giá trị của x để P có giá trị nguyên dương.
Bài 2: (3 điểm):
1. Giải hệ phương trình sau:
\(\left\{\begin{array}{l} \sqrt{2 x-1}-\dfrac{4}{x-y}=2 \\ 2 \sqrt{2 x-1}-\dfrac{6}{x-y}=5 \end{array}\right.\)
2. Cho các hàm số bậc nhất y = 2x - 3 và y = ax + b có đồ thị lần lượt là các đường thẳng d1 và d2.
a. Vẽ đồ thị của hàm số y = 2x -3
b. Xác định a, b để hai đường thẳng d1 ,d2 song song với nhau và d1, d2 lần lượt tạo với các trục Ox, Oy hai tam giác có tỉ số diện tích bằng 4.
Bài 3: (0.5 điểm) Nhà bạn Minh có một chiếc thang dài 4m. Cần đặt chân thang cách chân tường một khoảng cách bằng bao nhiêu để nó tạo được với mặt đất một góc “an toàn” là 65° (tức là đảm bảo thang không bị đổ khi sử dụng). (làm tròn đến chữ số thập phân thứ hai)
Bài 4: (3 điểm)
Cho đường tròn (O; R) và dây cung BC không đi qua tâm. Hai tiếp tuyến của (O;R) tại B và C cắt nhau ở A. Kẻ đường kính CD và kẻ BH vuông góc với CD tại Ha. Chứng minh 4 điểm A,B,O,C cùng thuộc một đường tròn
b. Chứng minh: OA // BD và BD² = DH . DC
c. Gọi I là giao điểm của BH và AD; M là giao điểm của BC và OA. Chứng minh: IM // CD
Bài 5: (0,5 điểm) Cho a, b, c là các số dương thỏa mãn điều kiện a + b + c = 1. Tìm giá trị nhỏ nhất của biểu thức :
\(\mathrm{P}=\sqrt{a^{2}+a b+b^{2}}+\sqrt{b^{2}+b c+c^{2}}+\sqrt{c^{2}+c a+a^{2}}\)
- Hết -
Vậy là cấu trúc đề thi thử tuyển sinh lớp 10 2022 môn Toán của trường Lương Thế Vinh lần thứ nhất đều không có nhiều thay đổi so với cấu trúc đề tuyển sinh vào lớp 10 các năm. Hãy thử sức làm bài trong thời gian 120 phút rồi so sánh đối chiếu với lời giải chi tiết dưới đây sau em nhé.
Đáp án đề thi thử vào 10 môn Toán Lương Thế Vinh lần 1 năm 2022
Bài 1: (3 điểm)
a, Với x = 9, ta có:
\(A=\dfrac{3 \sqrt{9}-1}{\sqrt{9}+1}\)
\(=\dfrac{3 \times 3-1}{3+1}\) \(=\dfrac{8}{4} = 2\)KL...
b, Với x ≥ 0; x ≠ 4 ta có:
\(B =\dfrac{2 \sqrt{x}}{\sqrt{x}+2}+\dfrac{3}{\sqrt{x}-2}+\dfrac{x+8}{4-x}\)
\(=\dfrac{2 \sqrt{x}(\sqrt{x}-2) + 3 (\sqrt{x}+2) - (x+8)}{(\sqrt{x}+2)(\sqrt{x}-2)}\)
\(=\dfrac{2 x - 4 \sqrt{x} + 3 \sqrt{x}+6 - x - 8}{(\sqrt{x}+2)(\sqrt{x}-2)}\)
\(=\dfrac{x - \sqrt{x} - 2}{(\sqrt{x}+2)(\sqrt{x}-2)}\)
\(=\dfrac{(\sqrt{x}+1)(\sqrt{x}-2)}{(\sqrt{x}+2)(\sqrt{x}-2)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)
KL...
c, Với x ≥ 0; x ≠ 4 ta có:
\(P = A.B = \dfrac{3 \sqrt{x}-1}{\sqrt{x}+1} .\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\) \( = \dfrac{3 \sqrt{x}-1}{\sqrt{x}+2} \)
\( =3 - \dfrac{7}{\sqrt{x}+2} \)
Ta dễ thấy \(\dfrac{7}{\sqrt x + 2} > 0\) với mọi x nên P < 3.
Để P có giá trị nguyên dương \(\Leftrightarrow \) P = 1 hoặc P = 2.
Với P = 1 \(\Leftrightarrow 3 - \dfrac{7}{\sqrt{x}+2} = 1\) \(\Leftrightarrow \dfrac{7}{\sqrt{x}+2} = 2\) \(\Leftrightarrow \sqrt{x}+2 = \dfrac{7}{2} \) \(\Leftrightarrow x = \dfrac{9}{4} \) (TM)
Với P = 2 \(\Leftrightarrow 3 - \dfrac{7}{\sqrt{x}+2} =2 \) \(\Leftrightarrow \dfrac{7}{\sqrt{x}+2} = 1\) \(\Leftrightarrow \sqrt{x}+2 = 7 \) \(\Leftrightarrow x = 25 \) (TM)
KL...
Bài 2: (3 điểm)
1. ĐKXĐ: \(x\geq\dfrac{1}2;x \neq y\)
\(\left\{\begin{array}{l} \sqrt{2 x-1}-\dfrac{4}{x-y}=2 \\ 2 \sqrt{2 x-1}-\dfrac{6}{x-y}=5 \end{array}\right.\)
\(\Leftrightarrow \left\{\begin{array}{l} \sqrt{2 x-1}= 4 \\ x-y = 2 \end{array}\right.\)
\(\Leftrightarrow \left\{\begin{array}{l} x = \dfrac{17}2 \\ y = \dfrac{13}2 \end{array}\right.\) (TM)
KL...
2. Cho các hàm số bậc nhất y = 2x - 3 và y = ax + b có đồ thị lần lượt là các đường thẳng d1 và d2.
a. Vẽ đồ thị của hàm số y = 2x -3
Học sinh tự vẽ
b.
Để d1 // d2 thì:
\(\left\{\begin{array}{l} a = 2 \\ b \neq -3 \end{array}\right.\)
Ta có diện tích tam giác tạo bởi d1, d2 với Ox Oy lần lượt là:
\(S_1 = \dfrac{1}2 |-3.\dfrac{3}2| = \dfrac{9}4\)
\(S_2 = \dfrac{1}2 |b.\dfrac{-b}2| = \dfrac{b^2}4\)
Theo bài ra ta có:
TH1: \(S_2 = 4 S_1 \Leftrightarrow \dfrac{b^2}{4} = 9 \Leftrightarrow \) b = 6 (tm) hoặc b = -6 (tm)
TH2: \(4S_2 = S_1 \Leftrightarrow b^2 = \dfrac{9}{4} \Leftrightarrow \) \(b = \dfrac{3}{2} \) (tm) hoặc \(b = \dfrac{-3}{2} \) (tm)
KL...
Bài 3: (0.5 điểm) Nhà bạn Minh có một chiếc thang dài 4m. Cần đặt chân thang cách chân tường một khoảng cách bằng bao nhiêu để nó tạo được với mặt đất một góc “an toàn” là 65° (tức là đảm bảo thang không bị đổ khi sử dụng). (làm tròn đến chữ số thập phân thứ hai)
Khoảng cách cần đặt X (từ chân thang tới chân tường) là:
\(X = 4 \times cos65^0\) (m)
KL...
Bài 4: (3 điểm)
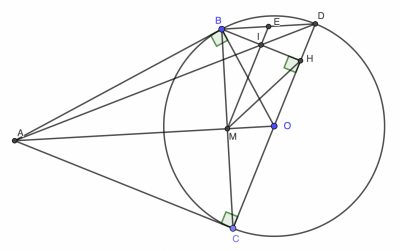
a. Chứng minh 4 điểm A,B,O,C cùng thuộc một đường tròn
Vì AB, AC là tiếp tuyến tại B, C của (O) nên ∠ABO = ∠ACO = 90⁰ ⇒ tứ giác ABOC nội tiếp (đpcm)
b. Chứng minh: OA // BD và BD² = DH . DC
Vì CD là đường kính của (O;R) nên ∠DBC = 90⁰ hay DB ⊥ BC. (1)
Dễ chứng minh 2 tam giác vuông △OAB = △OAC (vì OC = OB = R, OA chung, ∠ABO = ∠ACO = 90⁰)
⇒ AB = AC.
Ta lại có OB = OC ( = R) ⇒ OA là trung trực của BC ⇒ OA ⊥ BC. (2)
Từ (1) và (2) ⇒ OA // BD (đpcm)
c. Gọi I là giao điểm của BH và AD; M là giao điểm của BC và OA. Chứng minh: IM // CD
Bài 5: (0,5 điểm)
Áp dụng bất đẳng thức AM-GM cho cặp số dương a, b, ta có:
\(2ab \leq a^2 + b^2\)
\(\Leftrightarrow 3(a^2 + 2ab +b^2) \leq 4(a^2 + ab + b^2)\)
\(\Leftrightarrow 3(a+b)^2 \leq 4(a^2 + ab + b^2)\)
\(\Leftrightarrow \dfrac{\sqrt 3}{2}(a+b) \leq \sqrt{ a^2 + ab + b^2}\)
Tương tự, ta có:
\( \dfrac{\sqrt 3}{2}(b+c) \leq \sqrt{ b^2 + bc + c^2}\)
\( \dfrac{\sqrt 3}{2}(c+a) \leq \sqrt{ c^2 + ca + a^2}\)
Cộng vế với vế ta có:
\(P=\sqrt{a^{2}+a b+b^{2}}+\sqrt{b^{2}+b c+c^{2}}+\sqrt{c^{2}+c a+a^{2}} \geq \dfrac{\sqrt3}{2}(a+b+b+c + c +a)\)
\(\Leftrightarrow P \geq \sqrt3 (a+b+c) = \sqrt3 \)
Vậy \(min_P = \sqrt3 \Leftrightarrow a=b=c = \dfrac{1}3\)
KL...
-/-
Trên đây là hướng dẫn giải chi tiết đề thi thử vào 10 2022 môn toán lần 1 của trường Lương Thế Vinh, mong rằng đây sẽ là tài liệu hữu ích giúp các em ôn tập. Đừng quên còn rất nhiều tài liêu đề thi thử vào 10 môn toán khác của các tỉnh thành trên cả nước nhé.
