Đề thi thử THPT Quốc gia 2020 môn Toán có đáp án mã đề 114

Tuyển chọn đề thi thử THPT Quốc gia 2020 môn Toán mã đề 114 là đề thi khảo sát số 14 được Đọc Tài Liệu sưu tầm và biên soạn. Qua bộ đề sẽ giúp các em ôn tập kiến thức và các dạng đề thường xuyên ra:

Đề thi thử Toán mã 114

Câu 1: Số phức liên hợp của số phức \(z = 1 - 2i\) là

A.\(1 + 2i\).

B. \( - 1 - 2i\).

C. \(2 - i\).

D. \( - 1 + 2i\).

Câu 2: Đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y = \frac{{1 - x}}{{ - x + 2}}\) có phương trình lần lượt là

A.\(x = 1;\,y = 2\).

B. \(x = 2;\,y = 1\).

C. \(x = 2;\,y = \frac{1}{2}\).

D. \(x = 2;\,y =  - 1\)

Câu 3: Phương trình \({2^{2{x^2} + 5x + 4}} = 4\) có tổng tất cả các nghiệm bằng

A. \(1\).

B. \( - 1\).

C.\(\frac{5}{2}\).

D. \( - \frac{5}{2}\).

Câu 4: Tích phân \(\int\limits_0^1 {{e^{ - x}}{\rm{d}}x} \) bằng

A. \(e - 1\).

B.\(\frac{1}{e} - 1\).

C.\(\frac{{e - 1}}{e}\).

D.\(\frac{1}{e}\).

Câu 5: Trong không gian \(Oxyz\), phương trình mặt phẳng \(\left( {Oyz} \right)\) là

A.\(y + z = 0\)

B.\(z = 0\).

C. \(x = 0\).

D.\(y = 0\).

Câu 6. Một mặt cầu có diện tích \(16{\rm{\pi }}\) thì bán kính mặt cầu bằng

A. \(2\).

B. \(4\sqrt 2 \).

C. \(2\sqrt 2 \).

D. \(4\).

Câu 7. Số điểm cực trị của đồ thị hàm số \(y =  - {x^4} + 2{x^2} + 2\) là

A. \(2\).

B. \(3\).

C. \(0\).

D. \(1\).

Câu 8. Cho hình lăng trụ đứng có diện tích đáy là \(3{a^2}\), độ dài cạnh bên bằng 2a. Thể tích khối lăng trụ này bằng:

A. \(2{a^3}\).

B. \({a^3}\).

C. \(3{a^3}\).

D. \(6{a^3}\).

Câu 9. Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên dưới đây. Hàm số \(y = f\left( x \right)\) nghịch biến trên khoảng nào dưới đây?

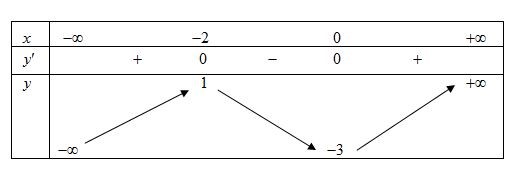
A. \(\left( { - 3;\;1} \right)\).

B. \(\left( {0;\; + \infty } \right)\).

C. \(\left( { - \infty ;\; - 2} \right)\).

D. \(\left( { - 2;\;0} \right)\).

Câu 10. Diện tích hình phẳng giới hạn bới hai đường thẳng \(x = 0\), \(x = {\rm{\pi }}\), đồ thị hàm số \(y = \cos x\) và trục Ox là

A. \(S = \int\limits_0^{\rm{\pi }} {\cos x\;{\rm{d}}x} \).

B. \(S = \int\limits_0^{\rm{\pi }} {{\rm{co}}{{\rm{s}}^2}x\;{\rm{d}}x} \).

C. \(S = \int\limits_0^{\rm{\pi }} {\left| {\cos x} \right|{\rm{d}}x} \).

D. \(S = \pi \int\limits_0^{\rm{\pi }} {\left| {\cos x} \right|{\rm{d}}x} \).

Câu 11: Trong không gian \(Oxyz\), cho mặt phẳng \((\alpha ):2x + y - z + 1 = 0\). Vectơ nào sau đây không là vectơ pháp tuyến của mặt phẳng \(\alpha \)?

A. \(\overrightarrow {{n_4}} \left( {4;2; - 2} \right)\).

B. \(\overrightarrow {{n_2}} \left( { - 2; - 1;1} \right)\).

C. \(\overrightarrow {{n_3}} \left( {2;1;1} \right)\).

D. \(\overrightarrow {{n_1}} \left( {2;1; - 1} \right)\).

Câu 12: Đường cong trong hình bên là đồ thị của hàm số nào dưới đây?

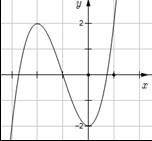
A. \(y = 2{x^3} + 6{x^2} - 2\)

B. \(y = {x^3} + 3{x^2} - 2\).

C. \(y =  - {x^3} - 3{x^2} - 2\).

D. \(y = {x^3} - 3{x^2} - 2\).

Câu 13: Họ nguyên hàm của hàm số \(y = \cos 3x\) là

A. \(\frac{{\sin 3x}}{3} + C\) (C là hằng số)

B. \( - \frac{{\sin 3x}}{3} + C\) (C là hằng số)

C. \(\sin 3x + C\) (C là hằng số)

D. \( - \sin 3x + C\) (C là hằng số)

Câu 14: Trong không gian Oxyz, cho hai điểm \(A\left( {1;\,2;\, - 1} \right)\) và \(B\left( { - 3;\,0;\, - 1} \right)\). Mặt phẳng trung trực của đoạn thẳng AB có phương trình là

A. \(x - y + z - 3 = 0\).

B. \(2x + y + 1 = 0\).

C. \(x - y + z + 3 = 0\).

D. \(2x + y - 1 = 0\).

Câu 15: \(\lim \frac{{1 - {n^2}}}{{2{n^2} + 1}}\) bằng

A. \(0\).

B. \(\frac{1}{2}\).

C. \(\frac{1}{3}\).

D. \( - \frac{1}{2}\).

Câu 16. Cho A, B là hai biến cố xung khắc. Đẳng thức nào sau đây đúng?

A. \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\).

B. \(P\left( {A \cup B} \right) = P\left( A \right).P\left( B \right)\).

C. \(P\left( {A \cup B} \right) = P\left( A \right) - P\left( B \right)\).

D. \(P\left( {A \cap B} \right) = P\left( A \right) + P\left( B \right)\).

Câu 17. Hàm số \(y = {\log _3}\left( {3 - 2x} \right)\) có tập xác định là

A. \(\left( {\frac{3}{2};\, + \infty } \right)\).

B. \(\left( { - \infty ;\frac{3}{2}\,} \right)\).

C. \(\left( { - \infty ;\frac{3}{2}} \right]\).

D. ℝ.

Câu 18. Gọi \({z_1}\) và \( {z_2}\) là 2 nghiệm của phương trình \(2{z^2} + 6z + 5 = 0\) trong đó \({z_2}\) có phần ảo âm. Phần thực và phần ảo của số phức \({z_1} + 3{z_2}\) lần lượt là

A. \( - 6;1\).

B.\( - 1; - 6\).

C. \( - 6; - 1\).

D. \(6;1\).

Câu 19. Cho hình lập phương ABCD.A'B'C'D' có Ovà O' lần lượt là tâm của hình vuông ABCD và A'B'C'D'. Gọi \({V_1}\) là thể tích khối nón tròn xoay có đỉnh là trung điểm của \(OO'\)và đáy là đường tròn ngoại tiếp hình vuông ABCD; \({V_2}\) là thể tích khối trụ tròn xoay có hai đáy là hai đường tròn nội tiếp hình vuông ABCD và A'B'C'D'. Tỉ số thể tích \(\frac{{{V_1}}}{{{V_2}}}\)

là

A. \(\frac{1}{2}\).

B. \(\frac{1}{4}\).

C. \(\frac{1}{6}\).

D. \(\frac{1}{3}\).

Câu 20. Biết \(\int\limits_0^1 {\frac{{2{x^2} + 3x + 3}}{{{x^2} + 2x + 1}}dx = a - \ln b} \) với a, b là các số nguyên dương. Tính \(P = {a^2} + {b^2}\).

A. 13.

B. 5.

C. 4.

D. 10

Câu 21: Trong không gian \(Oxyz\), cho đường thẳng \(d:\frac{{x + 1}}{1} = \frac{{y + 3}}{2} = \frac{{z + 2}}{2}\) và điểm \(A\left( {3;\,2;\,0} \right)\). Điểm đối xứng của điểm A qua đường thẳng d có tọa độ là

A. \(\left( { - 1;\,0;\,4} \right)\).

B. \(\left( {7;\,1;\, - 1} \right)\).

C. \(\left( {2;\,1;\, - 2} \right)\)

.D. \(\left( {0;\,2;\, - 5} \right)\).

Câu 22: Trong không gian \(Oxyz\), mặt phẳng chứa trục Oz và vuông góc với mặt phẳng \(\left( \alpha  \right):\,x - y + 2z - 1 = 0\) có phương trình là

A. \(x + y = 0\).

B. \(x + 2y = 0\).

C. \(x - y = 0\).

D. \(x + y - 1 = 0\).

Câu 23: Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình\(f\left( x \right) + m - 2018 = 0\)

 có 4 nghiệm phân biệt.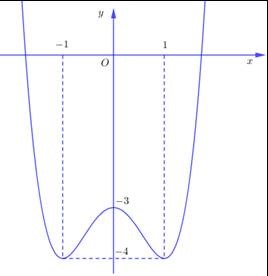

 

A. \(2021 \le m \le 2022\).

B. \(2021 < m < 2022\).

C. \(\left[ \begin{array}{l} m \ge 2022\\ m \le 2021 \end{array} \right.\).

D. \(\left[ \begin{array}{l} m > 2022\\ m < 2021 \end{array} \right.\).

Câu 24: Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right) = \frac{{x + 1}}{{x - 1}}\) trên đoạn \(\left[ {3;\,5} \right]\). Khi đó \(M - m\) bằng

A. \(\frac{7}{2}\).

B. \(\frac{1}{2}\).

C. 2.

D. \(\frac{3}{8}\).

Câu 25: Tiếp tuyến của đồ thị hàm số \(f\left( x \right) = \frac{1}{3}{x^3} - \frac{1}{2}{x^2} - 4x + 6\) tại điểm có hoành độ là nghiệm của phương trình \(f''\left( x \right) = 0\) có hệ số góc bằng

A. \( - 4\).

B. \(\frac{{47}}{{12}}\).

C. \( - \frac{{13}}{4}\).

D. \( - \frac{{17}}{4}\).

Câu 26: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách từ điểm A đến đường thẳng B'D' bằng

A. \(\frac{{a\sqrt 3 }}{2}\).

B. \(\frac{{a\sqrt 6 }}{3}\).

C.\(\frac{{a\sqrt 6 }}{2}\)

D. \(\frac{{a\sqrt 3 }}{3}\).

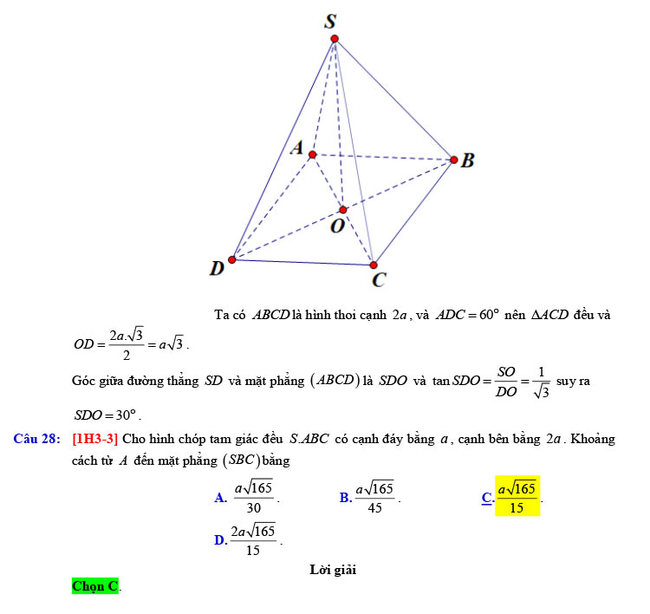
Câu 27: Cho hình chóp SABCD có đáy ABCD là hình thoi cạnh 2a, \(\widehat {ADC} = 60^\circ \). Gọi O là giao điểm của AC và BD, \(SO \bot \left( {ABCD} \right)\) và \(SO = a\). Góc giữa đường thẳng SD và mặt phẳng \(\left( {ABCD} \right)\) bằng

A. \(60^\circ \).

B. \(75^\circ \).

C. \(30^\circ \).

D. \(45^\circ \).

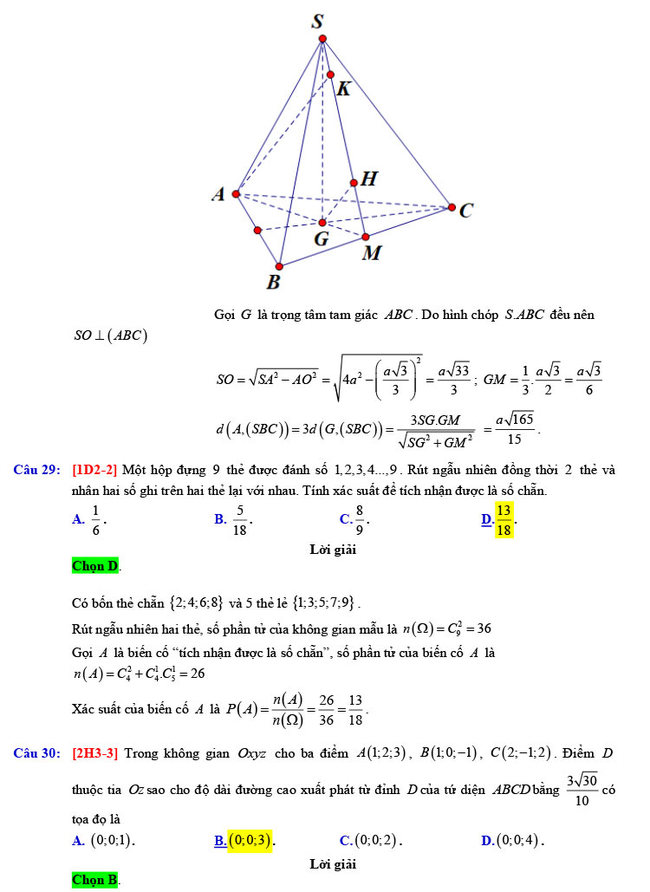
Câu 28: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, cạnh bên bằng 2a. Khoảng cách từ A đến mặt phẳng \(\left( {SBC} \right)\)bằng

A. \(\frac{{a\sqrt {165} }}{{30}}\).

B.\(\frac{{a\sqrt {165} }}{{45}}\).

C.\(\frac{{a\sqrt {165} }}{{15}}\).

D.\(\frac{{2a\sqrt {165} }}{{15}}\).

Câu 29: Một hộp đựng 9 thẻ được đánh số 1,2,3,4...,9. Rút ngẫu nhiên đồng thời 2 thẻ và nhân hai số ghi trên hai thẻ lại với nhau. Tính xác suất để tích nhận được là số chẵn.

A. \(\frac{1}{6}\).

B. \(\frac{5}{{18}}\).

C.\(\frac{8}{9}\).

D.\(\frac{{13}}{{18}}\).

Câu 30: Trong không gian Oxyz cho ba điểm \(A\left( {1;2;3} \right)\), \(B\left( {1;0; - 1} \right)\), \(C\left( {2; - 1;2} \right)\). Điểm D thuộc tia Oz sao cho độ dài đường cao xuất phát từ đỉnh D của tứ diện ABCD bằng \(\frac{{3\sqrt {30} }}{{10}}\) có tọa đọ là

A. \(\left( {0;0;1} \right)\).

B.\(\left( {0;0;3} \right)\).

C.\(\left( {0;0;2} \right)\).

D.\(\left( {0;0;4} \right)\).

Câu 31. Cho hàm số \(y = x - \ln \left( {1 + x} \right)\). Mệnh đề nào sau đây đúng?

A. Hàm số đồng biến trên khoảng \(\left( { - 1;\,0} \right)\).

B. Hàm số đạt cực đại tại x = 0.

C. Hàm số đồng biến trên khoảng \(\left( { - 1;\, + \infty } \right)\).

D. Hàm số đạt cực tiểu tại x = 0.

Câu 32. Tìm số nguyên dương n thỏa mãn \(C_{2n + 1}^1 + C_{2n + 1}^3 + ... + C_{2n + 1}^{2n + 1} = 1024\).

A. \(n = 10\).

B. \(n = 5\).

C. \(n = 9\).

D. \(n = 11\).

Câu 33. Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y = \left( {2m - 3} \right)x - \left( {3m + 1} \right){\rm{cos}}\,x\)

nghịch biến trên .

A. 1

B. 5

C. 0

D. 4

Câu 34. Cho \(I = \int\limits_0^m {\left( {2x - 1} \right){{\rm{e}}^{2x}}{\rm{d}}x} \). Tập hợp tất cả các giá trị của tham số m để \(I < m\) là khoảng \(\left( {a;\,b} \right)\). Tính \(P = a - 3b\).

A. \(P =  - 3\).

B. \(P =  - 2\).

C. \(P =  - 4\).

D. \(P =  - 1\).

Câu 35. Cho 4 số thực \(a,\,b,\,c,\,d\) là 4 số hạng liên tiếp của một cấp số cộng. Biết tổng của chúng bằng 4 và tổng các bình phương của chúng bằng 24. Tính \(P = {a^3} + {b^3} + {c^3} + {d^3}\).

A. \(P = 64\).

B. \(P = 80\).

C. \(P = 16\).

D. \(P = 79\).

Câu 36. Tổng tất cả các giá trị của tham số thực m sao cho đồ thị hàm số \(y = {x^3} - 3m{x^2} + 4{m^3}\) có điểm cực đại và cực tiểu đối xứng với nhau qua đường phân giác của góc phần tư thứ nhất là

A. \(\frac{{\sqrt 2 }}{2}\).

B. \(\frac{1}{2}\).

C. \(0\).

D. \(\frac{1}{4}\).

Câu 37. Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường \(x + y - 2 = 0\); \(y = \sqrt x \)

; \(y = 0\) quay quanh trục Ox bằng

A. \(\frac{5}{6}\).

B. \(\frac{{6\pi }}{5}\).

C. \(\frac{{2\pi }}{3}\).

D. \(\frac{{5\pi }}{6}\).

Câu 38. Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B, AB = a, BC = 2a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Gọi G là trọng tâm tam giác ABC, mặt phẳng \(\left( {SAG} \right)\) tạo với đáy một góc \(60^\circ \). Thể tích khối tứ diện ACGS bằng

A. \(V = \frac{{{a^3}\sqrt 6 }}{{36}}\).

B. \(V = \frac{{{a^3}\sqrt 6 }}{{18}}\).

C. \(V = \frac{{{a^3}\sqrt 3 }}{{27}}\).

D. \(V = \frac{{{a^3}\sqrt 6 }}{{12}}\).

Câu 39. Cho bất phương trình \({\log _7}\left( {{x^2} + 2x + 2} \right) + 1 > {\log _7}\left( {{x^2} + 6x + 5 + m} \right)\). Có bao nhiêu giá trị nguyên của tham số m để bất phương trình trên có tập ngiệm chứa khoảng \(\left( {1;\,3} \right)\)?

A. 35

B. 36

C. 34.

D. 33

Câu 40. Ông A đầu tư 150 triệu đồng vào một công ti với lãi 8% một năm và lãi hàng năm được nhập vào vốn ban đầu để tính lãi cho năm tiếp theo. Hỏi sau 5 năm số tiền lãi ông A rút về gần nhất với số tiền nào dưới đây, nếu trong khoảng thời gian này ông A không rút tiền ra và lãi không thay đổi?

A. 54.073.000 đồng.

B. 54.074.000 đồng.

C. 70.398.000 đồng.

D. 70.399.000 đồng.

Câu 41. Đường thẳng \(y = {m^2}\) cắt đồ thị hàm số \(y = {x^4} - {x^2} - 10\) tại hai điểm phân biệt A, B sao cho tam giác OAB vuông (O là gốc tọa độ). Mệnh đề nào sau đây đúng?

A. \({m^2} \in \left( {5;\,7} \right)\).

B. \({m^2} \in \left( {3;\,5} \right)\).

C. \({m^2} \in \left( {1;\,3} \right)\).

D. \({m^2} \in \left( {0;\,1} \right)\).

Câu 42. Trong không gian Oxyz, gọi \(I\left( {a;\,b;\,c} \right)\) là tâm mặt cầu đi qua điểm \(A\left( {1;\, - 1;\,4} \right)\) và tiếp xúc với tất cả các mặt phẳng tọa độ. Tính \(P = a - b + c\).

A. \(P = 6\).

B. \(P = 0\).

C. \(P = 3\).

D. \(P = 9\).

Câu 43: Cho số phức \(z = a + bi\) thỏa mãn \(\left| {z - 1 + 2i} \right| = 5\) và \(z.\bar z = 10\). Tính \(P = a - b\).

A. \(P = 4\).

B. \(P =  - 4\).

C. \(P =  - 2\).

D. \(P = 2\).

Câu 44: Cho hình lăng trụ \(ABC.A'B'C'\) có \(A'.ABC\) là tứ diện đều cạnh \(a\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(AA'\)

và \(BB'\). Tính tan của góc giữa hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {CMN} \right)\).

A. \(\frac{{\sqrt 2 }}{5}\).

B. \(\frac{{3\sqrt 2 }}{4}\).

C. \(\frac{{2\sqrt 2 }}{5}\).

D. \(\frac{{4\sqrt 2 }}{{13}}\).

Câu 45: Cho số phức \(z\) thỏa mãn \(\left| {z - 1 - i} \right| = 1\), số phức \(w\) thỏa mãn \(\left| {\bar w - 2 - 3i} \right| = 2\). Tìm giá trị nhỏ nhất của \(\left| {z - w} \right|\).

A. \(\sqrt {13}  - 3\).

B. \(\sqrt {17}  - 3\).

C. \(\sqrt {17}  + 3\).

D. \(\sqrt {13}  + 3\).

Câu 46. Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên , thỏa mãn \(2f\left( {2x} \right) + f\left( {1 - 2x} \right) = 12{x^2}\). Phương trình tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm có hoành độ bằng 1 là:

A. \(y = 2x + 2\).

B. \(y = 4x - 6\).

C. \(y = 2x - 6\).

D. \(y = 4x - 2\).

Câu 47. Trong một lớp có n học sinh gồm ba bạn Chuyên, Hà, Tĩnh cùng n - 3 học sinh khác. Khi xếp tùy ý các học sinh này vào dãy ghế được đánh số từ 1 đến n mỗi học sinh ngồi một ghế thì xác suất để số ghế của Hà bằng trung bình cộng số ghế của Chuyên và số ghế của Tĩnh là \(\frac{{13}}{{675}}\)

. Khi đó n thỏa mãn

A. \(n \in \left[ {35;39} \right]\).

B. \(n \in \left[ {40;45} \right]\).

C. \(n \in \left[ {30;34} \right]\).

D. \(n \in \left[ {25;29} \right]\).

Câu 48. Trong không gian Oxyz, cho ba điểm \(A\left( { - 1;0;1} \right)\), \(B\left( {3;2;1} \right)\), \(C\left( {5;3;7} \right)\). Gọi \(M\left( {a;b;c} \right)\) là điểm thỏa mãn \(MA = MB\) và \(MB + MC\) đạt giá trị nhỏ nhất. Tính \(P = a + b + c\)

A. \(P = 4\).

B. \(P = 0\).

C. \(P = 2\).

D. \(P = 5\).

Câu 49: Biết \(\int\limits_0^\pi  {\frac{{x{{\sin }^{2018}}x}}{{{{\sin }^{2018}}x + {{\cos }^{2018}}x}}{\mathop{\rm d}\nolimits} x}  = \frac{{{\pi ^a}}}{b}\) trong đó a, b là các số nguyên dương. Tính \(P = 2a + b\).

A. \(P = 8\).

B. \(P = 10\).

C. \(P = 6\).

D. \(P = 12\).

Câu 50: Cho phương trình:

\(\sin x\left( {2 - \cos 2x} \right) - 2\left( {2{{\cos }^3}x + m + 1} \right)\sqrt {2{{\cos }^3}x + m + 2}  = 3\sqrt {2{{\cos }^3}x + m + 2} \).

Có bao nhiêu giá trị nguyên của tham số m để phương trình trên có đúng 1 nghiệm \(x \in \left[ {0;\frac{{2\pi }}{3}} \right)\)?

A. \(2\).

B. \(1\).

C. \(4\).

D. \(3\).

Xem thêm đáp án từng câu hỏi dưới đây:

Đáp ánđề thi thử THPT Quốc gia 2020 môn Toán mã đề 114

Đáp án chi tiết của đề số 14 như sau:

1	B	11	C	21	A	31	D	41	C
2	A	12	B	22	A	32	B	42	D
3	D	13	A	23	B	33	B	43	A
4	C	14	B	24	B	34	A	44	C
5	C	15	D	25	D	35	A	45	B
6	A	16	A	26	C	36	C	46	D
7	B	17	B	27	C	37	D	47	D
8	D	18	C	28	C	38	A	48	D
9	D	19	D	29	D	39	C	49	A
10	C	20	A	30	B	40	D	50	D

Đáp án chi tiết đề thi thử THPT môn Toán năm 2020 mã 114

 

Trên đây là bộ đề thi thử thpt quốc gia 2020 môn Toán có đáp án Mã đề 114giúp các em ôn tập lại các kiến thức đã học, đánh giá năng lực làm bài của mình và chuẩn bị cho kì kiểm tra THPT sắp tới được tốt hơn với số điểm cao như mong muốn.

Chúc các em thi tốt!