Đề Toán minh họa 2020 toán do Bộ GD&ĐT công bố với đáp án do Đọc tài liệu thực hiện mong các em ôn tập kiến thức và các dạng đề thường xuyên ra:
Có thể tải đề thi thử này về với 2 định dạng PDF hoặc DOC để in ra phía dưới!
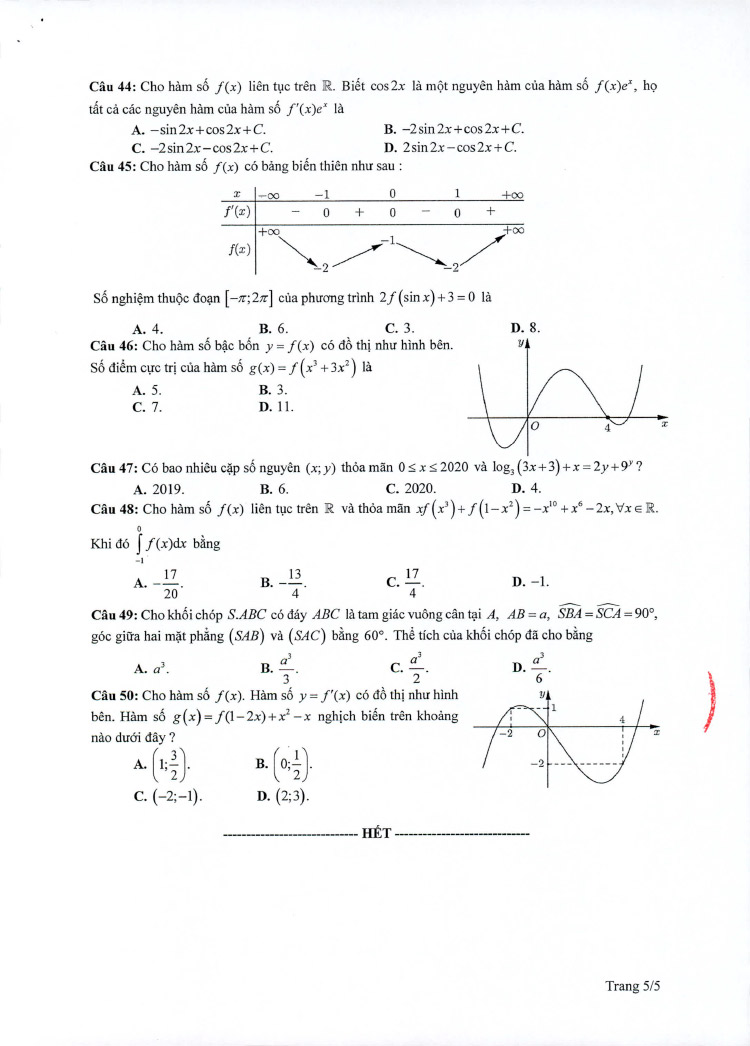
Đề thi Toán minh họa 2020




Đáp án tham khảo
| Câu | Đáp án | Câu | Đáp án | Câu | Đáp án | Câu | Đáp án | Câu | Đáp án |
|---|---|---|---|---|---|---|---|---|---|
| 1 | A | 11 | A | 21 | A | 31 | A | 41 | B |
| 2 | A | 12 | C | 22 | B | 32 | B | 42 | A |
| 3 | C | 13 | B | 23 | C | 33 | A | 43 | C |
| 4 | D | 14 | D | 24 | A | 34 | C | 44 | C |
| 5 | A | 15 | D | 25 | B | 35 | B | 45 | B |
| 6 | B | 16 | A | 26 | A | 36 | A | 46 | C |
| 7 | B | 17 | B | 27 | C | 37 | A | 47 | D |
| 8 | D | 18 | B | 28 | D | 38 | B | 48 | B |
| 9 | A | 19 | C | 29 | A | 39 | D | 49 | D |
| 10 | C | 20 | D | 30 | C | 40 | A | 50 | A |
Đáp án chi tiết 10 câu cuối đề thi
Câu 41:
\(log_9\,x=log_6\,y=log_4\,(2x+y)\)
\(\Leftrightarrow \left\{ \matrix{ log_9\,x=log_6 \,y \hfill \cr log_9 \,x= log_4 (2x+y) \hfill \cr} \right. \)\(\Leftrightarrow \left\{ \matrix{ log_9\,6\times log_6 \,x=log_6 \,y \hfill \cr log_9\,4\times log_4 \,x= log_4 (2x+y) \hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{ \frac{1}{2}log_3\,(3\times2) \times log_6 \,x=log_6 \,y \hfill \cr log_3\,2\times log_4 \,x= log_4 (2x+y) \hfill \cr} \right. \)\(\Leftrightarrow \left\{ \matrix{ \frac{1}{2}(1+log_3\,2) \times log_6 \,x=log_6 \,y \hfill \cr log_3\,2\times log_4 \,x= log_4 (2x+y) \hfill \cr} \right. \) \((1)\)
Đặt \(log_3\,2=a\), ta có \((1)\)\(\Leftrightarrow \left\{ \matrix{ \frac{1}{2}(1+a) \times log_6 \,x=log_6 \,y \hfill \cr a\times log_4 \,x= log_4 (2x+y) \hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{ x^{\frac{1}{2}(1+a)}= y \hfill \cr x^a= 2x+y \hfill \cr} \right. \)\(\Leftrightarrow \left\{ \matrix{ x^{\frac{1}{2}(1+a)}= y \hfill \cr x^a= 2x+x^{\frac{1}{2}(1+a)} \hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{ x^{\frac{1}{2}(1+a)}= y \hfill \cr x^a- 2x-x^{\frac{1}{2}(1+a)}=0 \hfill \cr} \right. \)\(\Leftrightarrow \left\{ \matrix{ x^{\frac{1}{2}(1+a)}= y \hfill \cr x^a- 2x-x^{\frac{a}{2}+\frac{1}{2}}=0 \hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{ x^{\frac{1}{2}(1+a)}= y \hfill \cr (x^{\frac{a}{2}}- 2x^{\frac{1}{2}})(x^{\frac{a}{2}}+x^{\frac{1}{2}})=0 \hfill \cr} \right. \). Vì x là số thực dương \( \Leftrightarrow \left\{ \matrix{ x^{\frac{1}{2}(1+a)}= y \hfill \cr x^{\frac{a}{2}}= 2x^{\frac{1}{2}} \hfill \cr} \right.\)
\( \Leftrightarrow \left\{ \matrix{ x^{\frac{1}{2}(1+a)}= y \hfill \cr x = 4^{\frac{1}{a-1}} \hfill \cr} \right.\)
\(\Rightarrow \frac{x}{y}=\frac{x}{x^{\frac{1}{2}(1+a)}} = x^{1-\frac{1}{2}-\frac{a}{2}}=x^{\frac{1}{2}-\frac{a}{2}}\)\(=4^{\frac{1}{a-1}({\frac{1}{2}-\frac{a}{2}})}=4^{\frac{-1}{2}}=\frac{1}{2}\) => Chọn đáp án B
Câu 42:
Ta có: \(f'(x)= \pm (3x^2-3)\)
\(f'(x)=0 \Leftrightarrow x = \pm 1\)
Vì ta chỉ xét trên đoạn \([0;3]\) \(\Rightarrow x =1\)
Vì f(x) là phương trình bậc 3, nên sẽ có 3 điểm cực trị lần lượt là f(0), f(1), f(3) trên đoạn đang xét.
Ta có:
\(f(0) = |m|\)
\(f(1) = |m-2|\)
\(f(3) = |18+m|\)
Vì giá trị cao nhất của f(x) trên đoạn \([0;3]\) là 16, với
\(f(0)=|m|=16 \Leftrightarrow \left[ \matrix{ m=16 \hfill \cr m=-16 \hfill \cr} \right. \) \(\Leftrightarrow \left[ \matrix{ {f(3)} = {34} \hfill \cr {f(1)} = {18} \hfill \cr} \right. \) (cả 2 giá trị đều > 16 => không thỏa mãn)
\(f(1)=|m-2|=16 \Leftrightarrow \left[ \matrix{ m=18 \hfill \cr m=-14 \hfill \cr} \right. \)\(\Leftrightarrow \left[ \matrix{ {f(3)} = {36} \hfill \cr m=-14(*) \hfill \cr} \right. \) (m = 18 không thỏa mãn, m = -14 thỏa mãn)
\(f(3)=|m+18|=16 \Leftrightarrow \left[ \matrix{ m=-2 \hfill \cr m=-34 \hfill \cr} \right. \)\(\Leftrightarrow \left[ \matrix{ m=-2 (*) \hfill \cr {f(1)} = {34} \hfill \cr} \right. \)(m = -34 không thỏa mãn, m = -2 thỏa mãn)
Vậy ta có m = -2 và m = -14 sẽ thỏa mãn yêu cầu đề bài, => S = -16 => Chọn đáp án A
Câu 43:
Ta có: \(log_2^2\,(2x ) - (m+2)log_2\,x +m-2=0\)
\(\Leftrightarrow ( log_2\,2+ log_2\,x )^2 - (m+2)log_2\,x +m-2=0\)
\(\Leftrightarrow (1+ log_2\,x )^2 - (m+2)log_2\,x +m-2=0\)
\(\Leftrightarrow log_2^2\,x - mlog_2\,x +m-1=0\)
\(\Leftrightarrow (log_2\,x -1) [log_2\,x -(m-1)]=0\)
\(\Leftrightarrow \left\{ \matrix{ log_2\,x=1 \hfill \cr log_2\,x=m-1 \hfill \cr} \right. \)
Để phương trình có 2 nghiệm phân biệt thuộc đoạn \([1;2]\)\(\Leftrightarrow \left\{ \matrix{ m-1\neq 1 \hfill \cr 0\leq m-1\leq1 \hfill \cr} \right. \)
\(\Leftrightarrow 0\leq m-1<1\Leftrightarrow 1\leq m<2\) => chọn đáp án C
Câu 44:
vì cos 2x là một nguyên hàm của hàm số \(f(x)e^x \) \(\Rightarrow (cos\,2x)'=f(x)e^x\Leftrightarrow f(x)e^x=-2sin\,2x \Leftrightarrow f(x)=\frac{-2sin\,2x}{e^x}\)
Ta có: \( f'(x)=\frac{-4cos\,2x\times e^x-e^x\times (-2sin\,2x)}{e^{2x}}=\frac{-4cos\,2x+ 2sin\,2x}{e^{x}}\)
\(\Leftrightarrow f'(x)e^x =-4cos\,2x+2sin\,2x\)
\(\Rightarrow \int f'(x)e^x\, \mathrm{d}x = \int(-4cos\,2x+2sin\,2x)\, \mathrm{d}x =-2sin\,2x-cos\,2x+C\)
=> Chọn đáp án CCâu 45:
Đặt \(sin\,x=t \in [-1;1]\). Dựa theo bảng biến thiên, kẻ đường thẳng \(y=-\frac{3}{2}\) cắt hàm số \(f(x)\) tại 2 điểm \(1<><>.
\(\Rightarrow 2f(t)+3=0 \Leftrightarrow t=x_1 \vee t = x_2\)
\(\Leftrightarrow \left[ \matrix{ sin\,x=x_1 \hfill \cr sin\,x = x_2 \hfill \cr} \right. \)
Ta đặt \(g(x) = 2f(sin\,x) + 3\) \(\Rightarrow g'(x) = 2f'(sin\,x)cos\,x\)
Ta vẽ đồ thị của \(sin\,x\) trên \([-\pi;2\pi]\) như hình dưới:
Đếm số nghiệm dựa vào hình trên, dễ thấy \(y=sin\,x=x_1\) có 4 nghiệm, \(y=sin\,x=x_2\) có 2 nghiệm nên tổng cộng \(2f(sin\,x)+3=0\) có 6 nghiệm thuộc đoạn \([-\pi;2\pi]\) => chọn đáp án B
Câu 46:
Dựa vào đồ thị, ta thấy có 3 điểm cực trị \(x_1<0<><>
Ta xét:
\(g'(x)=(3x^2+6x)f'(x^3+3x^2)=3x(x+2)f'(x^3+3x^2)\)
\(f'(x^3+3x^2)=0\) \(\Leftrightarrow \left[ \matrix{ x^3+3x^2=x_1 \hfill \cr x^3+3x^2=x_2 \hfill \cr x^3+3x^2=x_3 \hfill \cr} \right. \)
Dựa vào đồ thị trên ta thấy \(f'(x^3+3x^2)=0\) có 5 nghiệm đơn khác \(0\) và \(-2\) \(\Rightarrow g'(x)=0 \) có 7 nghiệm đơn phân biệt hay \(g(x)\) có đúng 7 cực trị
Câu 47:
Theo bài ra, ta có: \(0\leq x \leq 2020\) \(\Leftrightarrow\) \(log_3 \,3+0\leq log_3\,(3x+3)+x \leq log_3 \,6063+2020\)
\(\Leftrightarrow\) \(1\leq 2y+9^y < 2028\) \(\Rightarrow 1<9^y<2028 \Rightarrow 0 \leq y < 4\) (do \(9^4 > 2028 \))
Vì y nguyên \(\Rightarrow y \in \{0;1;2;3\}\)
Thay lần lượt giá trị của y, ta có:
\(y = 0 \Rightarrow x=0 \) (thỏa mãn)
\(y = 1 \Rightarrow x=8 \) (thỏa mãn)
\(y=2 \Rightarrow x=80\) (thỏa mãn)
\(y=3 \Rightarrow x=728 \) (thỏa mãn)
Vậy phương trình đã cho có 4 nghiệm nguyên thỏa mãn đề bài => chọn đáp án D
Câu 48:
\(xf(x^3)+f(1-x^2)=-x^{10}+x^6-2x\) \((1)\)
Gọi F(x) là một nguyên hàm của f(x), nhân cả hai vế của \((1)\) với x, ta có:
\(x^2f(x^3)+xf(1-x^2)=-x^{11}+x^7-2x^2\)
\(\Leftrightarrow \frac{F'(x^3)}{3}-\frac{F'(1-x^2)}{2}=-x^{11}+x^7-2x^2\) \((2)\)
\(\Rightarrow \int_{-1}^0 \frac{F'(x^3)}{3}dx- \int_{-1}^0\frac{F'(1-x^2)}{2}dx= \int_{-1}^0(-x^{11}+x^7-2x^2)dx\)
\(\Leftrightarrow \frac{F(0)-F(-1)}{3}- \frac{F(1)-F(0)}{2}= (\frac{-x^{12}}{12}+\frac{x^{8}}{8}-\frac{2x^{3}}{3})|_{-1}^0=\frac{-17}{24}\)
\(\Leftrightarrow \frac{5F(0)}{6}- \frac{F(-1)}{3}-\frac{F(1)}{2}= \frac{-17}{24}\) \((3)\)
Tương tự, ta có \((2)\) \(\Rightarrow \)
\(\Rightarrow \int_{0}^1 \frac{F'(x^3)}{3}dx- \int_{0}^1\frac{F'(1-x^2)}{2}dx= \int_{0}^1(-x^{11}+x^7-2x^2)dx\)
\(\Leftrightarrow \frac{F(1)-F(0)}{3}- \frac{F(0)-F(1)}{2}= (\frac{-x^{12}}{12}+\frac{x^{8}}{8}-\frac{2x^{3}}{3})|_{0}^1=\frac{-5}{8}\)
\(\Leftrightarrow \frac{-5F(0)}{6}+\frac{F(1)}{3}+\frac{F(1)}{2}= \frac{-5}{8}\) \((4)\)
\(\Leftrightarrow \frac{-5F(0)}{6}+\frac{5F(1)}{6}= \frac{-5}{8}\)
\(\Leftrightarrow F(0)-F(1)=\frac{3}{4}\)
Cộng hai vế của \((3)\) và \((4)\) với nhau, ta có:
\(\frac{F(1)}{3}-\frac{F(-1)}{3}= \frac{-5}{8}+\frac{-17}{24}\) \(\Leftrightarrow F(1)-F(-1)=-4\) \((5)\)
Ta cần tính: \(\int_{-1}^0f(x)dx =F(0)-F(-1)=F(0)-[F(1)+4]=\frac{3}{4}-4=\frac{-13}{4}\)
=> chọn đáp án B
Câu 49:
Ta có \(\triangle ABC \) vuông cân tại A \(\Rightarrow AB =AC\)
Xét \(\triangle SCA\) và \(\triangle SBA\), ta có \(\left\{ \matrix{ AB=AC \hfill \cr \angle SCA = \angle SBA = 90^0 \hfill \cr SA \,chung \hfill \cr} \right. \)
\(\Rightarrow \)\(\triangle SCA = \triangle SBA\) \((1)\)
Kẻ đường cao \(CH\) của \(\triangle SCA\) với \(H\in CA\) \((2)\)
Từ \((1)\) và \((2)\) dễ thấy \(\left\{ \matrix{ BH\perp SA \hfill \cr CH\perp SA \hfill \cr BH=CH \hfill \cr} \right. \)
\(\Rightarrow \) Góc giữa 2 mặt phẳng \((SAB)\) và \((SAC)\) chính là góc \(\angle CHB\) \(\Rightarrow \) \(\left[ \matrix{ \angle CHB=180^0-60^0=120^0 \hfill \cr \angle CHB=60^0\hfill \cr} \right. \)
Nếu \(\angle CHB=60^0\) \(\Rightarrow \) \(\triangle BHC\) là tam giác đều \(\Rightarrow \)\(BH=CH=BC=a\sqrt{2} > AC=BC=a\) (vô lý vì \(CH\) là đường cao của \(\triangle SCA\) vuông)
\(\Rightarrow \) \(\angle CHB=120^0\).
Xét \(\triangle CHB\) cân tại \(H\) có \(\angle CHB=120^0\), kẻ đường cao \(CK\) (\(K\in HB\)), ta dễ tính được:\(CK=\frac{1}{2}BC=\frac{a\sqrt{2}}{2}\) và \(\frac{BH}{sin\,30^0}=\frac{CH}{sin\,30^0}=\frac{BC}{sin\,120^0}\Leftrightarrow BH=CH=a\frac{\sqrt{6}}{3}\)
\(\Rightarrow \)\(AH=\frac{a\sqrt{3}}{3}\)
\(\Rightarrow \)\(AS=a\sqrt{3}\)Tính: \(S_{\triangle SAB}=\frac{1}{2}BH.AS=\frac{1}{2}\times a\frac{\sqrt{6}}{3}\times a\sqrt{3}=\frac{a^2\sqrt{2}}{2}\)
\(V_{S.ABC}=\frac{1}{3}S_{\triangle SAB} \times CK=\frac{1}{3}\times \frac{a^2\sqrt{2}}{2} \times \frac{a\sqrt{2}}{2}=\frac{a^3}{6}\) => chọn đáp án D
Câu 50:
Đặt \(t=1-2x\) \((1)\) , ta có:
\(g'(x)=2x-1-2f'(1-2x)=-t-2f'(t)\)
Để \(g(x)\) nghịch biến thì \(g'(x)=-t-2f'(t) \leq0 \Leftrightarrow f'(t) \geq\frac{-t}{2}\)
Dựa vào đồ thị trên của \(f'(x)\), ta thấy với \(t\in[-2;0]\) thì \(g'(x)\leq0\), kết hợp với \((1)\) ta có \(x\in[\frac{1}{2};\frac{3}{2}]\) thì \(g'(x)\leq0\) => chọn đáp án A
Xem thêm
Đề minh họa 2020 có đáp án full các môn:
- Đề minh họa môn Văn 2020
- Đề minh họa môn Anh 2020
- Đề minh họa môn Sinh 2020
- Đề minh họa môn Sử 2020
- Đề minh họa môn Địa 2020
- Đề minh họa môn GDCD 2020
- Đề minh họa môn Lý 2020
- Đề minh họa môn Hóa 2020
Trên đây là bộ đề thi thử thpt quốc gia 2020 môn Toán tham khảo mà Bộ công bố giúp các em ôn tập lại các kiến thức đã học, đánh giá năng lực làm bài của mình và chuẩn bị cho kì kiểm tra THPT sắp tới được tốt hơn với số điểm cao như mong muốn.
Chúc các em ôn thi thật tốt!




