NEW : Đáp án đề thi tuyển sinh lớp 10 môn Toán năm 2020 Đồng Nai
Sở GD&ĐT Đồng Nai chính thức công bố đề thi minh họa thi vào 10 môn Toán dành cho học sinh lớp 9 trên địa bàn tỉnh để giúp các em làm quen và thử sức với đề thi tại nhà. Đề thi chi tiết như sau:
Đề thi minh họa
|
SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỒNG NAI ĐỀ THI MINH HỌA |
KỲ THI TUYỂN SINH VÀO LỚP 10 NĂM HỌC 2020 - 2021 MÔN: TOÁN Thời gian làm bài: 120 phút |
Câu 1. (2 điểm)
1) Giải hệ phương trình
\(\left\{ \matrix{ 3x + 4y = -10 \hfill \cr 4x -5y = 28 \hfill \cr} \right.\)
2) Giải hai phương trình: \(2x^2 - x - 10 = 0\) và \(x^4 - 19x^2 + 48 = 0\).
3) Giải phương trình
\(\dfrac{1}{x-1} + \dfrac{6}{3x+5}= \dfrac{2}{x+2}+\dfrac{1}{x+3}\)
Câu 2. (2 điểm)
1) Vẽ đồ thị của hai hàm số \(y=\dfrac{-3}{2}x^2\), \(y= 2x- 2\) trên cùng một mặt phẳng tọa độ.
2) Tìm các tham số thực m để hai đường thẳng y = (m - 2)x + m và y = 2x - 2 song song với nhau.
3) Tìm các số thực x để biểu thức \(M = \sqrt{6 – 3x} - \dfrac{1}{\sqrt[3]{x^2-3x}}\) xác định.
Câu 3. (2 điểm)
1) Cho hình vuông MNPQ có MN = 4a, với \(0 < a ∈ ℝ\). Tính theo a diện tích xung quanh và thể tích của hình trụ tạo bởi hình vuông MNPQ quay quanh đường thẳng MN.
2) Cho phương trình \(2x^2 - 6x-1 = 0\) có hai nghiệm là \(x_1, x_2\). Tính \(P = |(x_1)^3- (x_2)^3| \). Lập một phương trình bậc hai một ẩn có hai nghiệm là \(x_1 - 2(x_2)^2\) và \(x_2 - 2(x_1)^2\)
3) Một chuyền may chỉ may một loại áo giống nhau và có kế hoạch may xong 4500 áo trong một thời gian quy định, với số áo may được trong mỗi ngày bằng nhau. Để hoàn thành sớm kế hoạch, mỗi ngày chuyền đã may nhiều hơn 400 áo so với số áo phải may trong một ngày theo kế hoạch, vì thể chuyền đã may xong 4500 áo sớm hơn kế hoạch 4 ngày. Tính số áo mỗi ngày chuyền may đã may trong thực tế.
Câu 4. (1 điểm)
1) Rút gọn biểu thức
\(P = \left(\dfrac{a+2\sqrt{a}}{2+\sqrt{a}}\right) \left(\dfrac{a-4\sqrt{a}+3}{\sqrt{a}-3}\right)\) (với \(0<>).
2) Tìm các số thực x và y thỏa mãn
\(\left\{ \matrix{ x^2 + y^2 = 9 \hfill \cr x^3 + y^3 = - 27 \hfill \cr} \right.\)
Câu 5. (2,5 điểm)
Cho tam giác nhọn ABC nội tiếp đường tròn (O) có ba đường cao AD, BE, CF cắt nhau tại trực tâm H.
1) Chứng minh bốn điểm A, E, H, F cùng thuộc một đường tròn.
2) Chứng minh BH.BE = BF.BA.
3) Gọi H' là điểm đối xứng của H qua BC. Chứng minh H' thuộc (O).
4) Chứng minh rằng H là tâm của đường tròn nội tiếp tam giác DEF.
Câu 6. (0,5 điểm) Cho ba số thực dương a, b, c. Chứng minh rằng
\(\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}≥4\left(\dfrac{a}{a+b}+\dfrac{b}{b+c}+\dfrac{c}{c+a}\right)\)
Hết
Vậy là Đọc tài liệu đã giới thiệu tới các em đề thi minh họa tuyển sinh vào 10 2020 môn Toán của tỉnh Đồng Nai, đừng quên còn rất nhiều tài liệu đề thi thử vào lớp 10 môn Toán khác đang đợi các em khám phá nhé!
Đáp án
Câu 1. (2 điểm)
1) \(\left\{ \matrix{ x = 2 \hfill \cr y = -4 \hfill \cr} \right.\)
2)
+) \(2x^2 - x - 10 = 0\)
⇔\(\left[ \begin{align}& x=-2 \\& x =\dfrac{5}{2} \\\end{align} \right.\\ \)
+) \(x^4 - x^2 + 48 = 0\).
⇔\(\left[ \begin{align}& x=±4 \\& x = ± \sqrt{3} \\\end{align} \right.\\ \)
3) ĐKXĐ: \(x ≠ \{1; -2; -3 ; \dfrac{-5}{3}\}\)
\(\dfrac{1}{x-1} + \dfrac{6}{3x+5}= \dfrac{2}{x+2}+\dfrac{1}{x+3}\)
\(\left[ \begin{align}& x=-1 \\& x = \dfrac{-17}{7} \\\end{align} \right.\\ \)
Câu 2. (2 điểm)
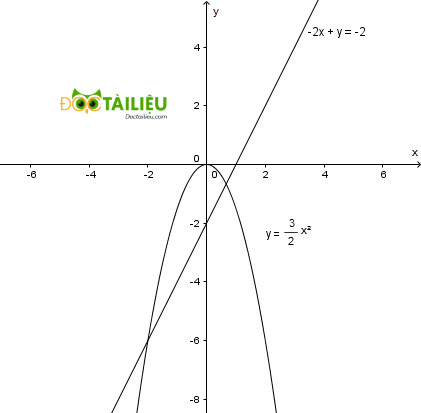
1) Vẽ đồ thị của hai hàm số \(y=\dfrac{-3}{2}x^2\), \(y= 2x- 2\) trên cùng một mặt phẳng tọa độ:
Lưu ý: Các em dựng bảng tọa độ điểm để vẽ.
2) Để hai đường thẳng y = (m - 2)x + m và y = 2x - 2 song song với nhau thì m phải thỏa mãn:
\(\left\{ \matrix{ m - 2 = 2 \hfill \cr m ≠ -2 \hfill \cr} \right. \) ⇒ \(m = 4\)
3) Điều kiện xác định
\(\left\{ \matrix{ 6 – 3x ≥ 0 \hfill \cr \sqrt[3]{x^2-3x} ≠0 \hfill \cr} \right. \) ⇔\(\left\{ \matrix{ x≤2 \hfill \cr x ≠ 0 \hfill \cr} \right. \)
Câu 3. (2 điểm)
1) Ta có:
\(V= 4a.\pi . (4a)^2 = 64 \pi a^3\)
2) Cho phương trình \(2x^2 - 6x-1 = 0\) có hai nghiệm là \(x_1, x_2\). Tính \(P = |(x_1)^3- (x_2)^3| \). Lập một phương trình bậc hai một ẩn có hai nghiệm là \(x_1 - 2(x_2)^2\) và \(x_2 - 2(x_1)^2\)
Áp dụng hệ thức Vi-ét cho phương trình đã cho, ta có:
\(\left\{ \matrix{ x_1+x_2 = 3 \hfill \cr x_1x_2 = \dfrac{-1}{2} \hfill \cr} \right. \)
Ta có:
\(P = |(x_1)^3- (x_2)^3| \) \(= \sqrt{(x_1^3- x_2^3)^2 }\)
\(= \sqrt{(x_1^3 + x_2^3)^2 -4x_1^3x_2^3 }\)
\(= \sqrt{(x_1 + x_2)^2 (x_1^2-x_1x_2+x_2^2)^2 -4x_1^3x_2^3 }\)
\(= \sqrt{(x_1 + x_2)^2 \left[(x_1+x_2)^2-3x_1x_2\right]^2 -4x_1^3x_2^3 }\)
\(= \sqrt{3^2 \left(3^2+\dfrac{3}{2}\right)^2 -4\left(\dfrac{-1}{2}\right)^3}\)
\(= \dfrac{19\sqrt{11}}{2}\)
Gọi hai nghiệm của phương trình cần lập là u và v. Ta có:
\(\left\{ \matrix{ u+v = x_1-2x_2^2 + x_2 - 2x_1^2 \hfill \cr uv = (x_1-2x_2^2)(x_2 - 2x_1^2) \hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{ u+v = ( x_1+ x_2)-2(x_1^2+x_2^2) \hfill \cr uv = x_1x_2 + 4x_1^2x_2^2 - 2 (x_1^3+x_2^3) \hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{ u+v = ( x_1+ x_2)-2(x_1+x_2)^2 +4x_1x_2 \hfill \cr uv = x_1x_2 + 4x_1^2x_2^2 - 2 (x_1+x_2)^3 + 6x_1x_2(x_1+x_2) \hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{ u+v = 3-2.3^2 -\dfrac{4}{2} =-17 \hfill \cr uv = \dfrac{-1}{2} + 4\left(\dfrac{-1}{2}\right)^2 - 2 .3^3 + 6.\left(\dfrac{-1}{2}\right).3 = \dfrac{-125}{2} \hfill \cr} \right. \)
Áp dụng hệ thức Vi-ét suy ra u và v là nghiệm của phương trình:
\(X^2 + 17 X - \dfrac{125}{2} = 0\)
3)
Gọi số áo mỗi ngày chuyền may đã may trong thực tế là x (\(x>400\))
Theo giả thiết ta có: \(\dfrac{4500}{x-400} - \dfrac{4500}{x} = 4\)
\(\Leftrightarrow 4x^2 - 1600 x - 1800000 = 0\)
\(\Leftrightarrow \) \(x=900\) (thoả mãn) hoặc \(x=-500\) (loại).
Câu 4. (1 điểm)
1) Rút gọn biểu thức
\(P = \left(\dfrac{a+2\sqrt{a}}{2+\sqrt{a}}\right) \left(\dfrac{a-4\sqrt{a}+3}{\sqrt{a}-3}\right)\) (với \(0 < a ≠ 9\)).
\(= \left[\dfrac{\sqrt{a}(\sqrt{a}+2)}{2+\sqrt{a}}\right] \left[\dfrac{(\sqrt{a}-3)(\sqrt{a}-1)}{\sqrt{a}-3}\right]\)
\(= \sqrt{a} (\sqrt{a}-1)\)
2)
\( \left\{ \matrix{ x^2 + y^2 = 9 \hfill \cr x^3 + y^3 = - 27 \hfill \cr} \right.\) (1)
Ta đặt:
\(\left\{ \matrix{ x+y = p \hfill \cr xy =q \hfill \cr} \right.\)
Biến đổi hệ đã cho thành dạng:
(1) \(\Leftrightarrow \left\{ \matrix{ p^2 - 2q = 9 \hfill \cr p^3 - 3pq = - 27 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ q = \dfrac{1}{2}(p^2 - 9) \hfill \cr p^3 - 3p.\dfrac{1}{2}(p^2 - 9) = -27 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ q = \dfrac{1}{2}(p^2 - 9) \hfill \cr p^3 - 27p - 54 = 0 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ q = \dfrac{1}{2}(p^2 - 9) \hfill \cr (p+3)^2(p-6) = 0 \hfill \cr} \right.\)
\(\Leftrightarrow \left[ \matrix{ p = -3 \Rightarrow q = 0 \hfill \cr p = 6 \Rightarrow q = \dfrac{27}{2} \hfill \cr} \right.\)
Với \((p;q) = (3;0)\) ta có:
\(\left\{ \matrix{ x+y = -3 \hfill \cr xy =0 \hfill \cr} \right.\) \(\Leftrightarrow \left[ \matrix{ (x;y) = (-3;0) \hfill \cr (x;y) = (0;-3) \hfill \cr} \right.\)
Với \((p;q) = \left(6;\dfrac{27}{2} \right)\) ta có:
\(\left\{ \matrix{ x+y = 6 \hfill \cr xy =\dfrac{27}{2} \hfill \cr} \right.\)
Thay ẩn vào ta được phương trình bậc 2 vô nghiệm.
Kết luận hệ đã cho có 2 cặp nghiệm \((x;y) = (0;-3)\) hoặc \((x;y) = (-3;0)\)
Câu 5. (2,5 điểm)
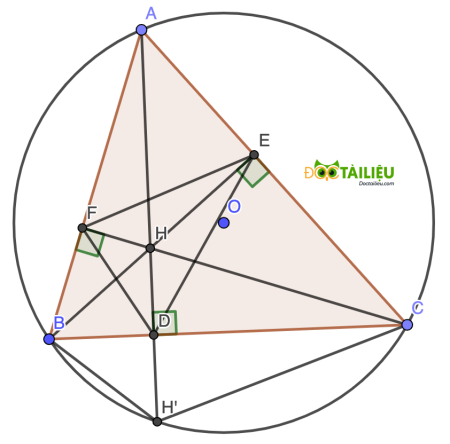
1)
Vì CF ⊥ AB và BE ⊥ AC (theo giả thiết) ⇒ ∠HEA = ∠HFA = 90⁰ ⇒ E và F cùng thuộc đường tròn đường kính AH hay bốn điểm A, E, H, F cùng thuộc một đường tròn (đpcm).
2)
Xét △BFH và △BEA, ta có:
Góc ∠FBH chung
∠BFH = ∠BEA = 90⁰ (giả thiết)
Suy ra △BFH ∽ △BEA ⇒ \(\dfrac{BF}{BH} = \dfrac{BE}{BA}\) ⇔ BH.BE = BF.BA (đpcm).
3)
Vì H' là điểm đối xứng của H qua BC ⇒ HH' ⊥ BC tại D và ∠BHD = ∠BH'D
Hay ∠BH'A = ∠BHD = 90⁰ - ∠HBD = 90⁰ - ∠EBC = ∠BCA ⇒ Tứ giác ABH'C nội tiếp, hay H' thuộc đường tròn (O) (đpcm).
4)
Xét tứ giác AEHF nội tiếp (chứng minh phần a) ⇒ ∠FEH = ∠FAH (góc nội tiếp cùng chắn cung FH) = 90⁰ - ∠AHF = 90⁰ - ∠DHC (góc đối đỉnh) = ∠HCD hay ∠FEH = ∠HCD (1)
Chứng minh tương tự ta được tứ giác CDHE nội tiếp ⇒ ∠HED = ∠HCD (góc nội tiếp cùng chắn cung HD) (2)
Từ (1) và (2) ⇒ ∠FEH = ∠HED hay EH là tia phân giác trong góc FED.
Chứng minh tương tự ta được FH là tia phân giác trong góc DFE.
Xét tam giác DEF có giao của ba tia phân giác trong tại H ⇒ H là tâm của đường tròn nội tiếp tam giác DEF (đpcm).
Câu 6. (0,5 điểm)
Ta có:
\(\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}+3≥4\left(\dfrac{a}{a+b}+\dfrac{b}{b+c}+\dfrac{c}{c+a}\right)\)
\(\Leftrightarrow \dfrac{a+b}{b}+\dfrac{b+c}{c}+\dfrac{c+a}{a}≥4\left(1- \dfrac{b}{a+b}+1-\dfrac{c}{b+c}+1-\dfrac{a}{c+a}\right)\) (*)
Ta cần chứng mình (*) đúng. Thật vậy:
Đặt \(\dfrac{a+b}{b} = z\), \(\dfrac{b+c}{c} = x\), \(\dfrac{c+a}{a} = y\) (với \(x,y,z >1\)) thay vào (*) ta có:
(*) \(\Leftrightarrow z+y+x≥4\left(1- \dfrac{1}{z}+1-\dfrac{1}{y}+1-\dfrac{1}{x}\right)\)
\(\Leftrightarrow x+\dfrac{4}{x}+y+\dfrac{4}{y}+z+\dfrac{4}{z}≥12\) (**)
Áp dụng bất đẳng thức AM-GM cho vế trái BĐT trên, ta có:
\(x+\dfrac{4}{x}+y+\dfrac{4}{y}+z+\dfrac{4}{z}≥2 \sqrt{x.\dfrac{4}{x}}+2 \sqrt{y.\dfrac{4}{y}}+2 \sqrt{z.\dfrac{4}{z}}\)
\(\Leftrightarrow x+\dfrac{4}{x}+y+\dfrac{4}{y}+z+\dfrac{4}{z}≥12\)
Hay (**) luôn đúng. Mà các phép biến đổi là tương đương nên ta có điều phải chứng minh.
Dấu = xảy ra \(\Leftrightarrow x=\dfrac{4}{x}\), \( y=\dfrac{4}{y}\), \( z=\dfrac{4}{z}\) \(\Leftrightarrow x=y=z= 2\) \(\Leftrightarrow a=b=c\).
Trên đây là đáp án đề thi minh họa tuyển sinh vào 10 môn Toán tỉnh Đồng Nai năm học 2020/2021, mong rằng với nội dung này các em sẽ thử sức đề thi thử vào lớp 10 và ôn luyện kiến thức thật tốt!
Đề thi minh họa môn khác:
