Số chính phương là một kiến thức các bạn sẽ gặp trong chương trình toán học phổ thông, dựa vào đặc điểm, tính chất của số chính phương sẽ phát triển thành các dạng bài toán khác nhau. Cùng tìm hiểu chi tiết, đầy đủ về số chính phương và ứng dụng bài tập về số chính phương.
Số chính phương và những kiến thức quan trọng về số chính phương
Đầu tiên chúng ta cùng xem lại chính xác về khái niệm, tính chất của số chính phương nhé.
1. Số chính phương là gì?
Số chính phương là số nguyên dương bằng bình phương đúng của một số nguyên.
n là số chính phương thì: \(n = k^2 \) (k thuộc Z)
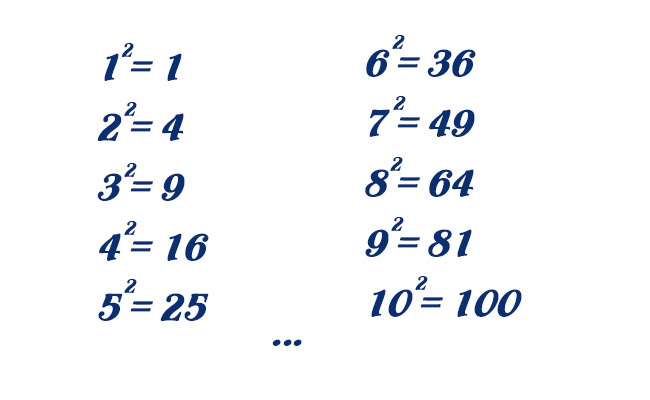
Hay hiểu cách khác:
Số chính phương là một số tự nhiên có căn bậc hai cũng là một số tự nhiên.
Số chính phương còn được gọi là số hình vuông (theo Số chính phương - Wikipedia.org). Số chính phương biểu thị diện tích của một hình vuông có chiều dài cạnh bằng số tự nhiên.
2. Đặc điểm và dấu hiệu nhận biết của số chính phương
Các đặc điểm của số chính phương sẽ được dùng để vận dụng giải các bài tập về số chính phương, nên các em cần ghi nhớ nhé.
- Số chính phương chỉ có chữ số tận cùng là 0,1,4,5,6,9, nếu các số tận cùng là 2,3,7,8 thì không phải là số chính phương.
- Khi phân tích ra thừa số nguyên tố, số chính phương chỉ chứa các thừa số nguyên tố với số mũ chẵn.
- Số chính phương chỉ có thể có 1 trong 2 dạng: 4n hoặc 4n + 1, không có số chính phương nào có dang 4n + 2 hoặc 4n + 3 (với n € N).
- Số chính phương chỉ có thể có 1 trong 2 dạng: 3n hoặc 3n + 1, không có số chính phương nào có dang 3n + 2 (với n € N).
- Số chính phương có chữ số tận cùng là 1 hoặc 9 thì chữ số hàng chục là chữ số chẵn.
+ Số chính phương tận cùng bằng 5 thì chữ số hàng chục là 2.
+ Số chính phương tận cùng bằng 4 thì chữ số hàng chục là chữ số chẵn.
+ Số chính phương tận cùng bằng 6 thì chữ số hàng chục là chữ số lẻ.
- Số chính phương chia hết đồng thời
+ Số chính phương chia hết cho 2 thì chia hết cho 4.
+ Số chính phương chia hết cho 3 thì chia hết cho 9.
+ Số chính phương chia hết cho 5 thì chia hết cho 25.
+ Số chính phương chia hết cho 8 thì chia hết cho 16.
- Mọi số chính phương chia cho 5, cho 8 dư 1, 0, 4.
- Giữa hai số chính phương liên tiếp không có số chính phương nào.
- Nếu hai số nguyên liên tiếp có tích là một số chính phương thì một trong hai số đó là 0.
- Số ước của một số chính phương là số lẻ. Ngược lại, một số có số các ước là số lẻ thì số đó là số chính phương.
- Nếu \(n^2<> (n thuộc Z) thì k không là số chính phương.
- Nếu hai số tự nhiên a và b nguyên tố cùng nhau có tích là một số chính phương thì mỗi số a, b cũng là các số chính phương.
- Nếu a là một số chính phương, a chia hết cho số nguyên tố p thì a chia hết cho \(p^2\)
- Nếu tích hai số a và b là một số chính phương thì các số a và b có dạng: \(a-mp^2; b-mq^2\)
- Số chính phương chia cho 3 không bao giờ có số dư là 2; chia cho 4 không bao giờ dư 2 hoặc 3; số chính phương lẻ khi chia 8 luôn dư 1.
Tất cả các số chính phương có thể viết thành dãy tổng của các số lẻ tăng dần từ 1 = 1, 4 = 1 + 3, 9 = 1 + 3 + 5, 16 = 1 + 3 + 5 + 7, 25 = 1 + 3 + 5 + 7 + 9, ...v.v
3. Bài tập chuyên đề số chính phương
Các dạng bài tập thường gặp về số chính phương
Dạng 1: Chứng minh một số là số chính phương, hoặc là tổng nhiều số chính phương.
Cơ sở phương pháp: Để chứng minh một số n là số là số chính phương ta thường dựa vào định nghĩa.
Ví dụ:
Cho n là một số tự nhiên. Chứng minh rằng: A= \(n(n+1)(n+2)(n+3)+1\) là số chính phương.
Hướng dẫn giản
Ta có:
\(A= (n^2+3n)(n^2+3n+2)+1\)
\(= (n^2+3n)^2+2n^2+3n+1=(n^2+3n+1)^2\)
Vì n thuộc N nên \(n^2+3n+1\) cũng thuộc N. Vậy A là số chính phương.
Dạng 2: Chứng minh một số không là số chính phương
Cơ sở phương pháp: Để chứng minh n không là số chính phương, tùy vào từng bài toán ta có thể sử dụng các cách sau:
+ Phương pháp 1. Chứng minh n không thể viết được dưới dạng một bình phương một số nguyên.
+ Phương pháp 2. Chứng minh \(k^2 < n < (k + 1)^2\) với k là số nguyên.
+ Phương pháp 3. Chứng minh n có tận cùng là 2; 3; 7; 8.
+ Phương pháp 4. Chứng minh n có dạng 4k + 2; 4k + 3.
+ Phương pháp 5. Chứng minh n có dạng 3k + 2.
+ Phương pháp 6. Chứng minh n chia hết cho số nguyên tố p mà không chia hết cho p^2.
Ví dụ
Chứng minh rằng số \(A=n^4+2n^3+2n^2+2n+1\) trong đó n thuộc N và n>1 không phải số chính phương.
Hướng dẫn giải
Ta có:
\(A=n^4+2n^3+2n^2+2n+1\)=\(n^4+2n^3+n^2+n^2+1\)
=\((n^2+n)^2+(n+1)^2>(n^2+n)^2\) với mọi n>1.
=> \(A> (n^2+n)^2\) với mọi n >1.
Mặt khác
\((n^2+n+1)^2 = n^2+2n^3+n^2+1\)
\(=n^4+2n^3+2n^2+2n+1+n^2\)
= \(A+n^2>A\) với mọi n>1
=> \(A<(n^2+n+1)^2\)
Ta có \((n^2+n) và (n^2+n+1)\) là hai số tự nhiên liên tiếp nên A không thể là số chính phương.
Dạng 3: Điều kiện để một số là số chính phương.
Cơ sở phương pháp: Chúng ta thường sử dụng các phương pháp sau:
+ Phương pháp 1: Sử dụng định nghĩa.
+ Phương pháp 2: Sử dụng tính chẵn, lẻ.
+ Phương pháp 3: Sử dụng tính chất chia hết và chia có dư.
+ Phương pháp 4: Sử dụng các tính chất.
Ví dụ:
Tìm số nguyên n sao cho n+1955 và n+2014 là một số chính phương.
Hướng dẫn giải
Giả sửa \(n+1955=a^2\), \(n+2014=b^2\) với a, b thuộc N và \(a<>.
Khi đó \(b^2-a^2=59\)
\(\Leftrightarrow (b-a)(b+a)=59 \).
Do 59 là số nguyên tố nên ta tiếp tục có
\(\left\{\begin{matrix} b-a=1\\ b+a=59 \end{matrix}\right.\)
=> a=29, b=30
=> n= -1114
Dạng 4: Tìm số chính phương
Cơ sở phương pháp: Dựa vào định nghĩa về số chính phương A = \(k^2\) với k là số nguyên và các yêu cầu của bài toán để tìm ra số chính phương thỏa bài toán.
Ví dụ:
Tìm số chính phương \(\overline{abcd}\) biết \(\overline{ab}-\overline{cd}=1\)
Hướng dẫn giải
Giả sử \(n^2=\overline{abcd}=100\overline{ab}+\overline{cd}\)
\(=100(1+\overline{cd})+cd=101\overline{cd}+100\), n thuộc Z.
=> \(101\overline{cd}=n^2-100=(n-10)(n+10)\)
Vì \(n<100\) và 101 là sô nguyên nên n+10=101
=> \(n=91\)
Thử lại: \(\overline{abcd}=91^2=8281\), có 82-81=1
Vậy \(\overline{abcd}=8281\)
4. Ứng dụng bài toán số chính phương trong C++ và Python
Kiểm tra số chính phương trong C/C++
Bài toán: Hãy viết chương trình nhập vào số nguyên dương n. Kiểm tra xem n có phải là số chính phương hay không? (số chính phương là số khi lấy căn bặc 2 có kết quả là nguyên). Hãy viết chương trình kiểm tra số chính phương sử dụng ngôn ngữ C++
Hướng dẫn giải
using namespace std;
int main(){
int n;
cout \(<<\) "\nNhap n = ";
cin \(>>\) n;
int i = 0;
while(i*i <= n){
if(i*i == n){
cout \(<<\) n \(<<\) " la so chinh phuong!\n";
return 0;
}
++i;
}
cout \(<<\) n \(<<\) " khong phai so chinh phuong!\n";
}
Out put
4 la so chinh phuong!
Kiểm tra số chính phương bằng Python
Bài toán: Hãy viết chương trình nhập vào số nguyên dương n. Kiểm tra xem n có phải là số chính phương hay không?
n = int(input())
check = False
for i in range(1, n + 1 ):
if (i**2 == n):
check = True
break
if (check == True):
print(n, " là số chính phương")
else:
print(n, " không phải là số chính phương")
Out put
Nhập vào số N lớn hơn 0:
4
4 là số chính phương
-/-
Với những kiến thức về số chính phương ở trên sẽ giúp bạn có cái nhìn tổng quát về số chính phương, từ đó giúp bạn tìm cách xử lí nhanh nhất những bài toán về số chính phương trong cả toán học và tin học một cách dễ dàng.
