Kiến thức trọng tâm về hình chóp đều và các dạng bài

Tổng hợp kiến thức trọng tâm về hình chóp đều, cách tính diện tích, thể tích cùng những dạng bài về hình chóp đều từ cơ bản tới nâng cao.

I. Hình chóp đều

Hình chóp đều là gì? Có mấy loại hình chóp đều? Cùng Đọc tài liệu tham khảo dưới đây về định nghĩa và phân loại hình chóp đều nhé.

1. Định nghĩa hình chóp đều

Đường cao được vẽ từ đỉnh của mỗi mặt bên của hình chóp đều gọi là trung đoạn của hình chóp đó.

2. Công thức tính diện tích xung quanh của hình chóp đều

Sxq = p.d trong đó: p - nửa chu vi đáy, d - chiều cao của mặt bên (trung đoạn)

3. Công thức tính diện tích toàn phần của hình chóp đều:

Stp = Sxq + Sđ

4. Thể tích hình chóp đều:

V = 1/3S.h, trong đó S - diện tích đáy, h - chiều cao.

II. Các loại hình chóp đều thường gặp

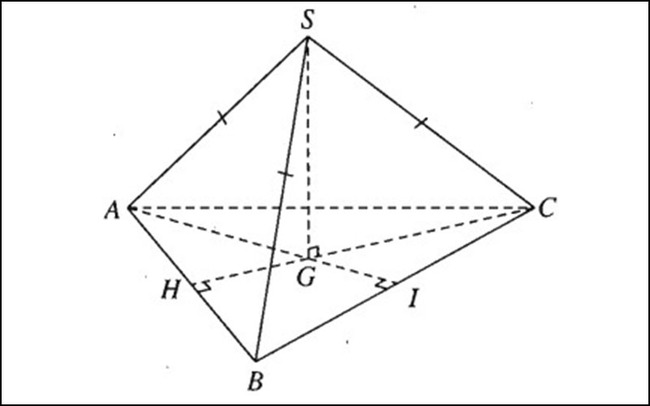
1. Hình chóp tam giác đều

a. Định nghĩa:

b. Đặc điểm của hình chóp tam giác đều:

• Hình chóp tam giác đều có 3 mặt phẳng đối xứng.
• Các cạnh bên bằng nhau.
• Tất cả các mặt bên là các tam giác cân bằng nhau.
• Chân đường cao trùng với tâm mặt đáy (tâm đáy là trọng tâm của tam giác).
• Tất cả các góc tạo bởi các mặt bên và mặt đáy đều bằng nhau.
• Tất cả các góc tạo bởi cạnh bên và mặt đáy đều bằng nhau.

c. Cách vẽ hình chóp tam giác đều

Dưới đây là các bước để các bạn có thể vẽ hình chóp tam giác đều nhanh chóng và dễ dàng nhất:

• Bước 1: Vẽ đáy là hình tam giác đều
• Bước 2: Vẽ các cạnh bên sao cho bằng nhau
• Bước 3: Vẽ các mặt bên với các tam giác cân bằng nhau
• Bước 4: Chân đường cao sẽ trùng với chân của đáy
• Bước 5: Góc tạo bởi cạnh bên (mặt đáy) và mặt đáy bằng nhau

d. Thể tích hình chóp tam giác đều:

\(V_{S.ABC}=\frac{1}{3}S_{ABC}.SH\)

Trong đó:

\(S_{ABC}\) là diện tích đáy tam giác đều ABC

SH là chiều cao của hình chóp.

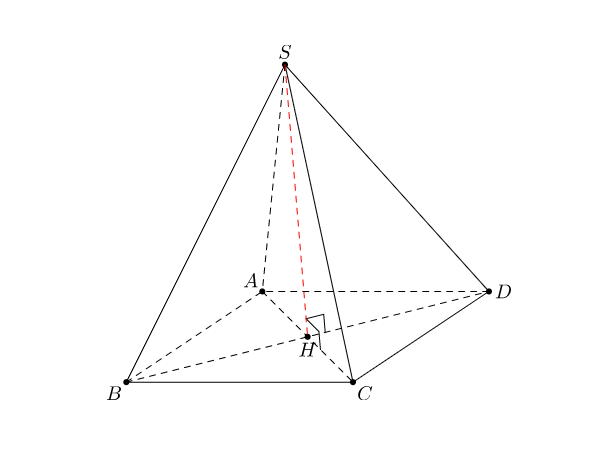
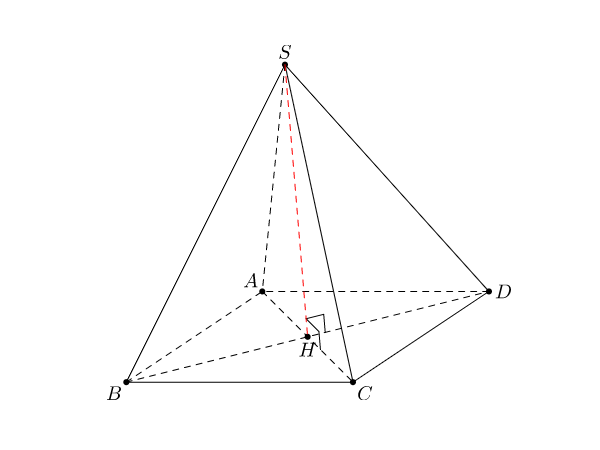
2. Hình chóp tứ giác đều

a. Định nghĩa:

b. Đặc điểm của hình chóp tứ giác đều:

• Tất cả các mặt bên là các tam giác cân bằng nhau.
• Chân đường cao trùng với tâm mặt đáy (tâm đáy là giao điểm 2 đường chéo).
• Tất cả các góc tạo bởi cạnh bên và mặt đáy bằng nhau.

c. Cách vẽ hình chóp tứ giác đều.

Dưới đây là cách vẽ hình chóp tứ giác đều chi tiết nhất qua các bước sau:

• Bước 1: Vẽ đáy là hình vuông
• Bước 2: Vẽ các cạnh bên bằng nhau
• Bước 3: Vẽ các mặt bên là các tam giác cân bằng nhau
• Bước 4: Chân đường cao trùng với tâm của mặt phẳng đáy
• Bước 5: Góc tạo bởi cạnh bên (mặt đáy) và mặt đáy bằng nhau

d. Thể tích hình chóp tứ giác đều:

\(V_{S.ABCD}=\frac{1}{3}S_{ABCD}.SH\)

Trong đó:

\(S_{ABCD}\) là diện tích đáy tứ giác đều ABCD

SH là chiều cao của hình chóp.

III. Các dạng bài toán hình chóp đều

Dạng 1: Xác định mối quan hệ giữa các yếu tố của hình chóp

Xác định mối quan hệ giữa các yếu tố của hình chóp như cạnh, mặt phẳng… trong hình chóp đều và hình chóp cụt đều.

Phương pháp giải:

1. Ta sử dụng mối quan hệ song song và vuông góc của các đường thẳng, các mặt phẳng, các đường thẳng và mặt phẳng với nhau
2. Ta sử dụng kiến thức về hình chóp đều.

Ví dụ:

Cho hình chóp tứ giác đều S.ABCD, gọi O là giao điểm của AC và BD.

a.Chứng minh rằng \(SO\perp (ABCD)\).

b.Chứng minh rằng \((SAC)\perp (SBD)\)

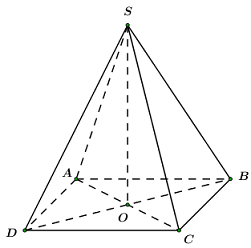
Hướng dẫn: Dựa vào định nghĩa của hình chóp đều.

Giải:

a. Ta lần lượt có:

Trong SAC, ta có: \(SA=SC \Leftrightarrow \Delta SAC\)  cân tại S =>  \(SO\perp AC\)(1)

Trong SBD, ta có: \(SB=SD\Leftrightarrow \Delta SAC\) cân tại S, \(SO \perp BD\) (2)

Từ (1),(2) suy ra \(SO \perp(ABCD)\)

b.

Từ kết quả câu a), ta có: \(SO \perp AC\) (3)

Mặt khác, vì ABCD là hình vuông nên \(BD \perp AC\) (4)

Từ (3) và (4) suy ra: \((SBD  ) \perp AC \in SAC\) => \((SAC) \perp (SBD)\).

Dạng 2: Xác định định lượng của các yếu tố trong hình chóp

Xác định độ dài của cạnh, diện tích xung quanh, diện tích toàn phần và thể tích của hình chóp đều hoặc hình chóp cụt đều.

Phương pháp giải:

1. Sử dụng công thức như sau: Sxq = p.d (với p là nửa chu vi đáy, d là trung đoạn)
2. Diện tích toàn phần sẽ bằng tổng của diện tích xung quanh và diện tích đáy
3. Đối với hình chóp, để xác định được diện tích xung quanh thì ta tính tổng diện tích của các mặt bên
4. Để tính diện tích xung quanh một hình chóp cụt đều, hãy tính diện tích một mặt bên và nhân nó với số mặt bên hoặc trừ diện tích xung quanh hình chóp nhỏ với diện tích xung quanh hình chóp.
5. Thể tích của hình chóp bằng một phần ba của diện tích đáy nhân với chiều cao: \(V = \frac{1}{3}S.h\).

Ví dụ:

Yêu cầu:

a. Tính thể tích của hình chóp đều (h.136)

b. Tính diện tích xung quanh hình chóp cụt đều (h.137)

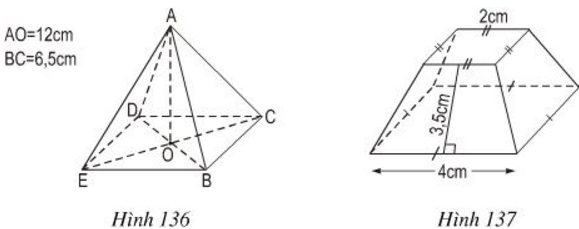
Giải:

a. Diện tích đáy của hình chóp đều:

\(S_{BCDE}=BC^2={6,5}^2=42,25 cm^2\)

Thể tích hình chóp đều là:

\(V_{A.DCBE}=\frac{1}{3}S_{BCDE}.h=\frac{1}{3}.42,25.12=169cm^3\)

b. Các mặt xung quanh là những hình thang cân đáy nhỏ 2cm, đáy lớn 4cm, chiều cao 3,5 cm.

Diện tích xung quanh của hình chóp cụt đều là:

\(S_{xq}= 4. \frac{(2+4).3,5}{2} = 42 cm^2.\)

-/-

Trên đây là toàn bộ nội dung kiến thức trọng tâm về hình chóp đều trong chương trình hình học, cùng với các dạng bài tập về hình chóp đều thường gặp để các em phân loại dạng bài và luyện tập tốt nhất. Chúc các em học tốt.