Bạn đang tìm kiếm tài liệu tổng hợp kiến thức về hình chóp đều và hình chóp cụt đều? Hãy tham khảo ngay bài viết dưới đây của Đọc tài liệu với những lý thuyết hình chóp đều và hình chóp cụt đều cùng tổng hợp các dạng toán cơ bản thường gặp. Đây sẽ là tài liệu học tập hữu ích cho học sinh và đồng thời giúp các thầy cô có thêm tài liệu hay phục vụ việc dạy học.
Cùng tham khảo nhé!

I. Lý thuyết về Hình chóp đều và hình chóp cụt đều
1. Hình chóp
- Hình chóp có mặt đáy là một đa giác và các mặt bên là những tam giác có chung một đỉnh. Đỉnh này gọi là đỉnh của hình chóp
- Đường thẳng đi qua đỉnh và vuông góc với mặt phẳng đáy gọi là đường cao của hình chóp.
- Hình chóp có đáy là tam giác gọi là hình chóp tam giác
- Hình chóp có đáy là tứ giác gọi là hình chóp tứ giác.
Trên hình dưới đây ta có hình chóp \(S.ACBD, SH \bot {\rm{mp}}\left( {ABCD} \right),\) \(S\) là đỉnh, \(SH\) là đường cao của hình chóp.
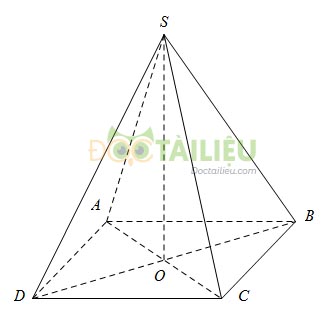
2. Hình chóp đều
Hình chóp đều là hình chóp có mặt đáy là một đa giác đều, các mặt bên là những tam giác cân bằng nhau có chung đỉnh (là đỉnh của hình chóp đều).

Trên hình ta có hình chóp tứ giác đều, \(SO\) là đường cao, \(O\) là tâm của đường tròn đi qua các đỉnh của lục giác \(ABCD\)
Đường cao \(SK\) của mặt bên gọi là trung đoạn của hình chóp.
+ Khi cắt hình chóp đều bởi mộ mặt phẳng song song với đáy, phần hình chóp nằm giữa hai mặt phẳng đó và mặt phẳng đáy của hình chóp gọi là hình chóp cụt đều.
Mỗi mặt bên của hình chóp cụt đều là một hình thang cân.
Trên hình dưới đây, ta có hình chóp cụt tứ giác đều \(ABCD.A'B'C'D'\).
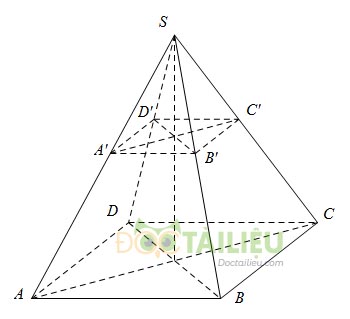
II. Các dạng toán thường gặp
Dạng 1: Xác định mối quan hệ giữa các yếu tố (cạnh, mặt phẳng…) trong hình chóp đều, hình chóp cụt đều.
Phương pháp:
+ Sử dụng mối quan hệ song song và vuông góc giữa các đường thăng, các mặt phẳng, giữa đường thẳng và mặt phẳng.
+ Sử dụng kiến thức về hình chóp đều
III. Bài tập mẫu
Hình chóp tứ giác đều \(S.ABCD\) có các mặt bên là những tam giác đều, \(AB = 8m, O\) là trung điểm của \(AC.\)
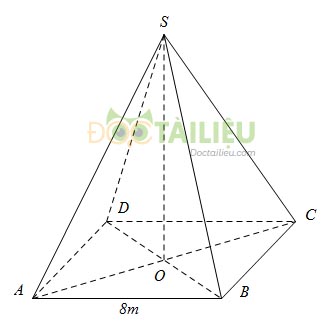
Độ dài đoạn \(SO\) là bao nhiêu?
Lời giải
Hình chóp tứ giác đều \(S.ABCD\) nên đáy \(ABCD\) là hình vuông nên \(∆ OAB\) vuông cân tại \(O\)
Áp dụng định lí Py-ta-go vào tam giác vuông \(∆ OAB\) ta có:
\(A{B^2} = O{A^2} + O{B^2}\)
\(\Rightarrow A{B^2} = 2O{A^2}\)
\(\Rightarrow OA = \sqrt {\dfrac{{A{B^2}}}{2}} = \sqrt {\dfrac{{{8^2}}}{2}} = \sqrt {32} \left( m \right)\)
Hình chóp có các mặt bên là các tam giác đều nên \(\Delta SAB\) là tam giác đều, do đó \(SA=AB=8m\).
Ta có \(SO ⊥ OA\) nên tam giác \(SOA\) vuông tại \(O\)
Áp dụng định lí Py-ta-go vào tam giác vuông \(SOA\) ta có:
\(\begin{array}{l} S{A^2} = O{S^2} + O{A^2}\\ \Rightarrow OS = \sqrt {S{A^2} - O{A^2}} \\ \Rightarrow OS = \sqrt {{8^2} - 32} = \sqrt {32} \,\left( m \right) \end{array}\)
=>> Xem thêm nhiều bài tập khác trong chuyên đề hình chóp đều và hình chóp cụt đều lớp 8 để củng cố kiến thức và rèn luyện kỹ năng làm bài
*********************
Trên đây là tổng hợp lý thuyết hình chóp đều và hình chóp cụt đều và các dạng bài thường gặp bao gồm các kiến thức cần nắm và cách làm các dạng bài tập liên quan mà Đọc tài liệu đã tổng hợp. Hy vọng đây sẽ là tài liệu học tập hữu ích cho các em học sinh cũng như các phụ huynh trong quá trình dạy học cho con em mình tại nhà. Ngoài ra đừng quên xem thêm những kiến thức khác và cách giải Toán 8 được cập nhật liên tục tại doctailieu.com. Chúc các em luôn học tốt và đạt kết quả cao!