Đề thi tuyển sinh vào lớp 10 môn toán vòng 1 năm học 2022 - 2023 trường THPT Chuyên KHTN được cập nhật nhanh nhất!
Đề thi vào lớp 10 môn toán 2023 vòng 1 trường chuyên KHTN

Đề thi tuyển sinh môn toán vào lớp 10 vòng 1 chuyên KHTN 2022

Đáp án





Đề thi tuyển sinh môn toán vào lớp 10 vòng 1 chuyên KHTN 2021
Câu I: Giải phương trình
\(13 \sqrt{5-x}+18 \sqrt{x+8}=61+x+3 \sqrt{(5-x)(x+8)}\)
Câu II. Giải hệ phương trình
\(\left\{\begin{array}{l} x^{4}+y^{4}+6 x^{2} y^{2}=1 \\ x(x+y)^{4}=x-y \end{array}\right.\)
Câu III. Tìm số nguyên dương n nhỏ nhất, biết rằng khi chia n co 7, 9, 11, 13 ta nhận được các số dư tương ứng là 3, 4, 5, 6.
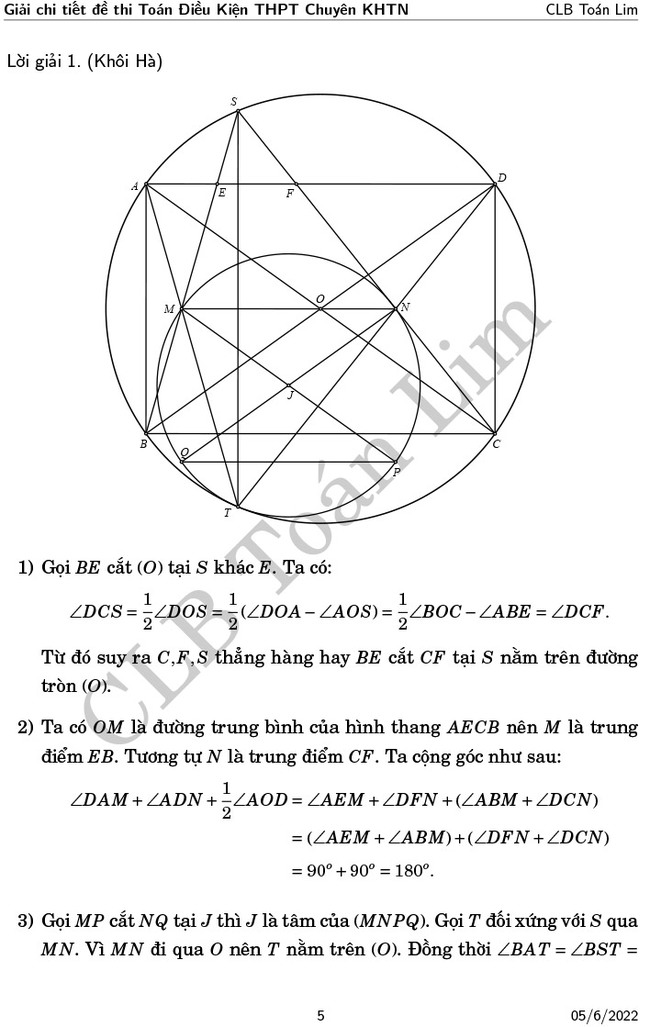
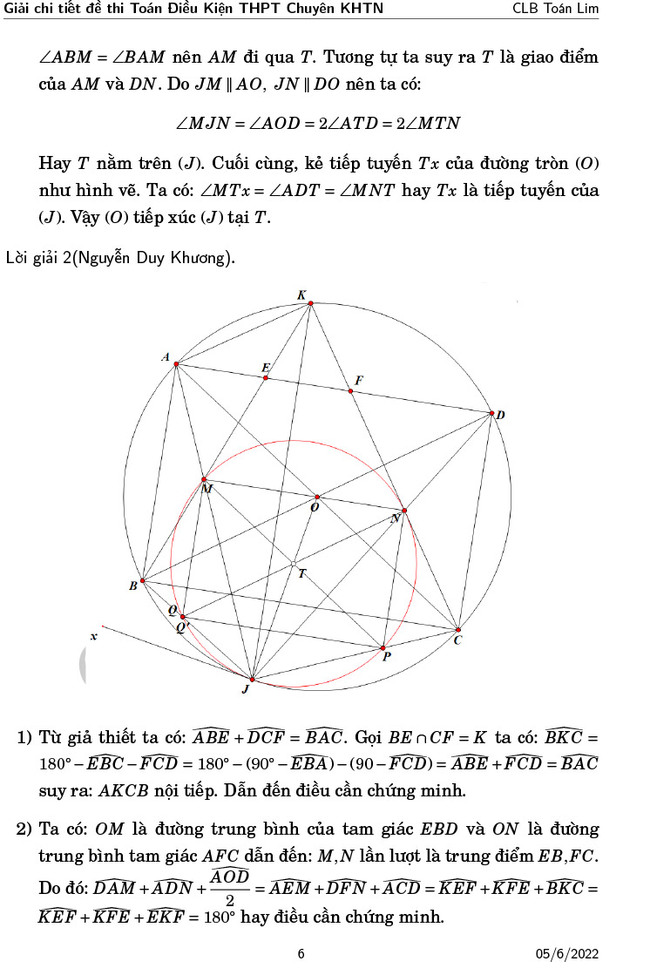
Câu IV. Cho tam giác nhọn ABC có điểm P nằm trong tam gác (P không nằm trên các cạnh). Gọi J, K, L lần lượt là tâm đường tròn nội tiếp các tam giác PBC, PCA. PAB.
1) Chứng minh rằng \( \widehat{B J C}+\widehat{C K A}+\widehat{A L B}=450^{\circ}\)
2) Giả sử PB = PC và \(PC < PA\). Gọi X, Y, Z lần lượt là hình chiếu vuông góc của J, K, L trên các cạnh B C, CA, AB. Dựng hình bình hành XYWZ. chứng minh rằng W nằm trên phân giác \(\widehat{B A C}\) .
Câu V. Cho tập \(A=\{1,2,3, \ldots, 2021\}\) . Tìm số nguyên dương k lớn nhất (k>2) sao cho ta có thể chọn được k số phân biệt từ tập A mà tổng của hai số phân biệt bất kỳ trong k số được chọn không chia hết cho hiệu của chúng.

Đáp án đề thi môn toán vào lớp 10 vòng 1 chuyên KHTN 2021




Câu 5:
Dễ thấy nếu trong k số chọn ra có 2 số liên tiếp sẽ không thỏa mãn (Vì hiệu 2 số = 1, tổng luôn chia hết)
tương tự, nếu trong k số chọn ra có 2 số chẵn liên tiếp (hoặc lẻ liên tiếp) sẽ ko thỏa mãn (vì hiệu 2 số = 2, tổng 2 số chẵn (hoặc lẻ) là số chẵn chia hết cho 2)
Vậy k số chọn ra không được gồm 2 số tự nhiên liên tiếp hoặc 2 số cách nhau 2 đơn vị.
Ta đi chứng minh với k = 674 là đúng.
Với k > 674, theo nguyên lý Dirichlet ta có 675 * 3 - 1= 2024 > 2021 ⇒ trong k số luôn tồn tại ít nhất 1 cặp số cách nhau 1 hoặc 2 đơn vị ⇒ không thỏa mãn (chứng minh trên)
Với k = 674, ta tìm ra dãy số có 674 phần tử thỏa mãn là {1;4;7;10; ...;3k+1;... ; 2020}
Ta đi chứng minh dãy số trên thỏa mãn yêu cầu đề bài. Thật vậy, gọi 2 số bất kì trong dãy trên sẽ có dạng 3k + 1 và 3h + 1 (k,h ∈ ℕ)
Tổng = 3 (k + h) + 2
Hiệu = 3 (k - h)
dễ thấy hiệu ⋮ 3 mà tổng không ⋮ 3 ⇒ Tổng không chia hết cho hiệu hay dãy trên là thỏa mãn.
Kết luận k = 674.
-/-
Trên đây là toàn bộ nội dung của đề thi tuyển sinh lớp 10 môn toán chung năm 2021 của trường chuyên KHTN và một số thông tin về kỳ thi vào lớp 10 được Đọc Tài Liệu chia sẻ.
Mong rằng những tài liệu của chúng tôi sẽ là người đồng hành giúp các bạn hoàn thành tốt bài thi của mình.
