Đọc tài liệu tổng hợp đề thi tuyển sinh vào 10 môn toán chuyên năm 2017 trường Lê Hồng Phong, Nam Định mời các em cùng thử sức với đề thi này.
Đề thi vào 10 môn toán chuyên năm 2017 trường Lê Hồng Phong
SỞ GIÁO DỤC VÀ ĐÀO TẠO NAM ĐỊNH ĐỀ CHÍNH THỨC | ĐỀ THI TUYỂN SINH LỚP 10 TRƯỜNG THPT CHUYÊN Năm học: 2017-2018 Môn: TOÁN (chuyên) Thời gian làm bài: 150 phút. (Đề thi gồm: 01 trang) |
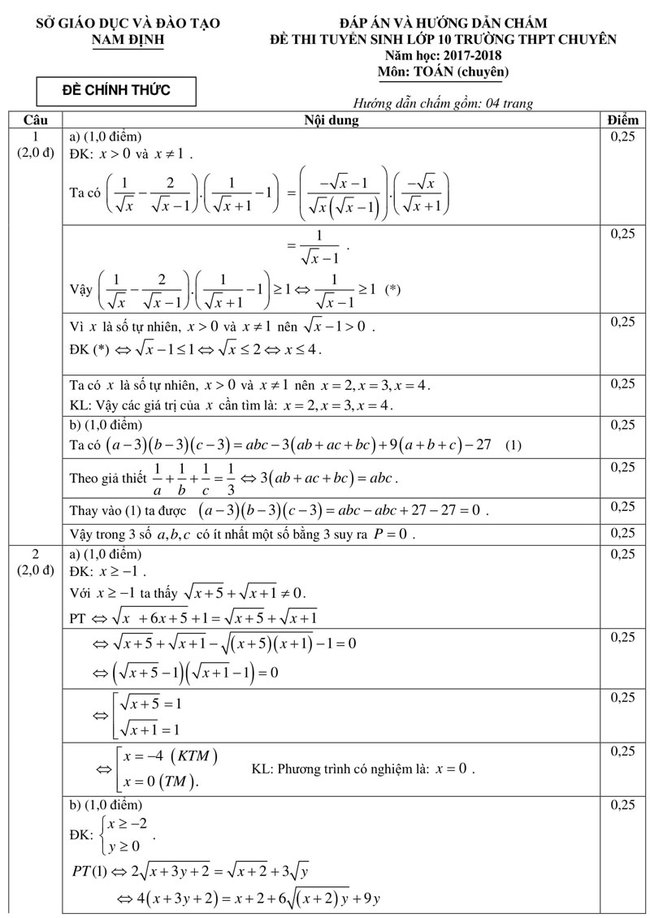
Câu 1. (2,0 điểm)
a. Tìm tất cả các số tự nhiên x thỏa mãn \((\frac{1}{\sqrt{x}}-\frac{2}{\sqrt{x}-1})(\frac{1}{\sqrt{x}+1}-1)\geq 1\)
b. Với a,b,c là các số thực thỏa mãn các điều kiện a+b+c = 3 và \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{3}\)
Tính giá trị biểu thức \(P=(a-3)^{2017}.(b-3)^{2018}.(c-3)^{2019}\)
Câu 2. (2,0 điểm)
a. Giải phương trình \((\sqrt{x+5}-\sqrt{x+1})(\sqrt{x^2+6x+5}+1)=4.\)
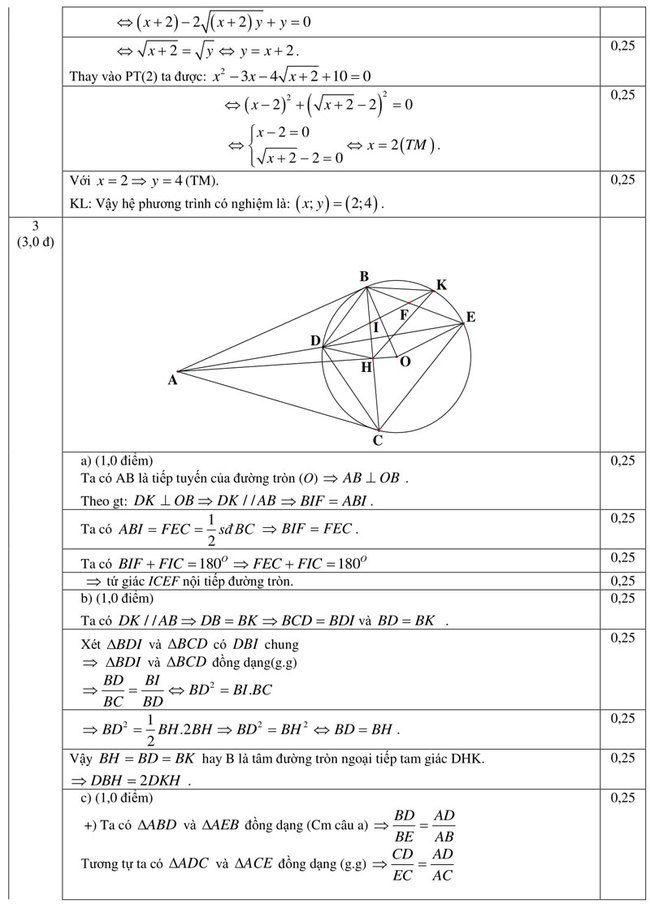
b. Giải hệ phương trình \(\left\{\begin{matrix} 2\sqrt{x+3y+2}-3\sqrt{y}=\sqrt{x+2}\\ x^2-3x-4\sqrt{y}+10=0 \end{matrix}\right.\)
Câu 3. (3,0 điểm)
Cho đường tròn (O), từ điểm A nằm ngoài đường tròn (O) kẻ hai tiếp tuyến AB, AC với đường tròn (O) (B, C là các tiếp điểm). Gọi H là giao điểm của AO và BC, I là trung điểm của BH. Đường thẳng qua I vuông góc với OB cắt đường tròn (O) tại hai điểm D, K (D thuộc cung nhỏ BC). Tia AD cắt đường tròn (O) tại điểm thứ hai là E. DK cắt BD tại F.
a. Chứng minh ICEF là tứ giác nội tiếp.
b. Chứng minh \(DBH = 2.DKH\) .
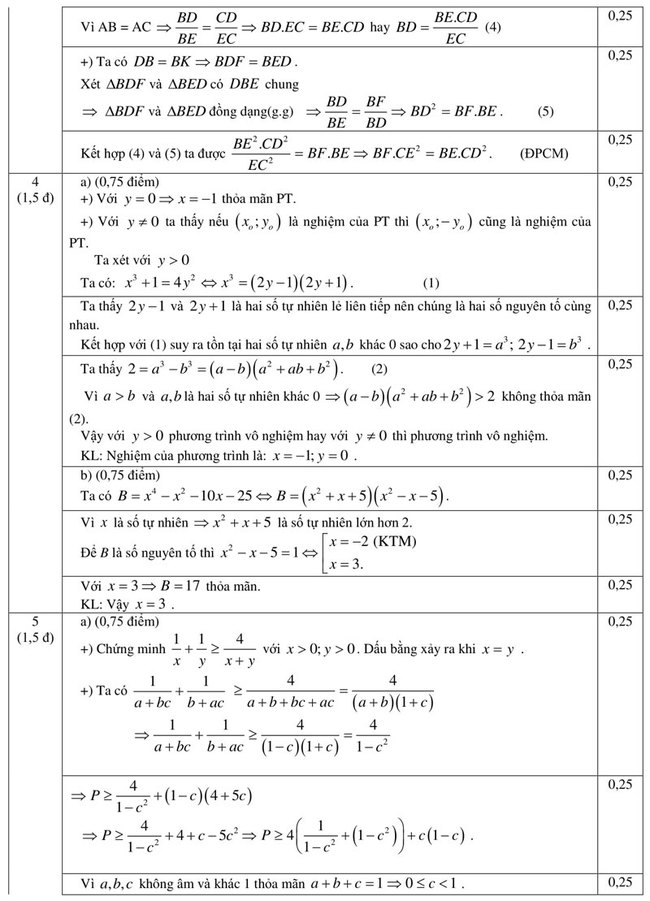
c. Chứng minh rằng: \(BD.CE = BE.CD\) và \(BF.CE^2 = BE.CD^2\).
Câu 4. (1,5 điểm)
a. Tìm các số nguyên x, y thỏa mãn phương trình \(x^3 +1=4y^2\).
b. Tìm tất cả các số tự nhiên x để biểu thức \(B = x^4-x^2 – 10x – 25\) là số nguyên tố.
Câu 5. (1,5 điểm) a. Xét các số thực a,b,c không âm, khác 1 và thỏa mãn a+b+c=1. Tìm giá trị nhỏ nhất của biểu thức \(P=\frac{1}{a+bc}+\frac{1}{b+ac}+(a+b)(4+5c)\)
b. Cho tứ giác ABCD nội tiếp đường tròn (O) bán kính R = 4cm (điểm O nằm trong tứ giác ABCD). Xét 33 điểm phân biệt nằm trong tứ giác ABCD sao cho không có 3 điểm nào thẳng hàng. Chứng minh rằng trong số 33 điểm đó luôn tìm được 3 điểm là 3 đỉnh của một tam giác có diện tích nhỏ hơn \(\frac{3\sqrt{3}}{4}cm^2\).
---------HẾT----------
Đáp án đề thi toán chuyên vào 10 năm 2017 trường Lê Hồng Phong - Nam Định

-/-
Với đầy đủ đề thi cùng đáp án đề thi vào lớp 10 năm 2017 môn toán chuyên trường Lê Hồng Phong, Nam Định hi vọng các em có thể rèn luyện được các phản xạ với với nhiều dạng kiến thức, rèn luyện kĩ năng nhận dạng đề bài và tìm ra cách giải tối ưu nhất. Chúc các em thi tốt trong kì thi tuyển sinh vào 10 sắp tới.