Trường THPT Chuyên Khoa học tự nhiên đưa ra đề kiểm tra kiến thức lớp 9 để các em làm quen dạng đề thi thử môn Toán Chung vào 10. Bài thi có 4 câu, thời gian làm bài 120 phút.
Cùng thử sức rồi so sánh đáp án em nhé!
Đề thi thử
Câu I.
1. Giải phương trình:
\(6\sqrt{2x+5} - 2\sqrt{x-1} = x + 14\)
2. Giải hệ phương trình:
\(\left\{ \matrix{ \dfrac{4}{x+y} + \dfrac{6}{y} = \dfrac{3}{x} \hfill \cr 3x^2 + y^2 = x + 3y \hfill \cr} \right.\)
Câu II.
1. Tìm số tự nhiên có ba chữ số \(n = \overline{xyz}\) sao cho \(2.(\overline{xyz}-2) = \overline{xy}^2 - z^2\)
2. Với các số thực dương a, b thỏa mãn điều kiện a + b = 4, tìm giá trị nhỏ nhất của:
\(P = \dfrac{1}{(a+2b)^2} + \dfrac{1}{(b+2a)^2} \)
Câu III.
Cho tam giác ABC nhọn với \(AB < AC\) và nội tiếp đường tròn (O). Tiếp tuyến qua A của (O) cắt BC tại T. E, F lần lượt là hình chiếu của T lên đường thẳng CA, AB.
1. Chứng minh rằng EF ⊥ BC
2. Gọi M, N lần lượt là trung điểm BC, EF. H là trực tâm tam giác ABC. Chứng minh rằng AN và HM cắt nhau tại một điểm trên (O).
Câu IV. Cho các số thực a,b,c. Chứng minh rằng
\(\dfrac{\sqrt{bc}}{a + 2\sqrt{bc}} + \dfrac{\sqrt{ca}}{b + 2\sqrt{ca}} + \dfrac{\sqrt{ab}}{c + 2\sqrt{ab}} ≤ 1\)
Hết
Trên đây là đề thi thử vào lớp 10 môn Toán của trường THPT chuyên KHTN với mẫu Toán thi chung vào chuyên, hãy thử sức trước rồi so sánh kết quả dưới đây sau em nhé!
Đáp án
Câu I
1. Điều kiện x ≥ 1, biến đổi phương trình về dạng
\(2x + 5 - 6\sqrt{2x+5} + 9 = x - 2\sqrt{x-1} \)
\(\Leftrightarrow (\sqrt{2x+5} - 3)^2 = (\sqrt{x-1} - 1)^2\) (1)
Trường hợp 1:
(1) \(\Leftrightarrow \sqrt{2x+5} - 3 = \sqrt{x-1} - 1\)
\(\Leftrightarrow \sqrt{2x+5} = \sqrt{x-1} +2\)
bình phương hai vế thu được
\(x + 2 = 4\sqrt{x-1}\)
\(\Leftrightarrow x^2 - 12x + 20 = 0\)
Kết quả: x ∈ {2, 10} (thỏa mãn).
Trường hợp 2:
(1) \(\Leftrightarrow \sqrt{2x+5} - 3 = - (\sqrt{x-1} - 1)\)
\(\Leftrightarrow \sqrt{2x+5} - 3 + \sqrt{x-1} - 1 = 0\)
Từ đó ta biến đổi
\(\Leftrightarrow (x - 2)(\dfrac{2}{\sqrt{2x+5} + 3} + \dfrac{1}{\sqrt{x-1} + 1}) = 0\)
\(\Leftrightarrow x = 2\) (thỏa mãn)
Bởi vậy tập nghiệm của phương trình là S = {2, 10} .
2)
Điều kiện x ≠ 0, y ≠ 0, x + y ≠ 0, quy đồng biến đổi phương trình thứ nhất của hệ thành:
\(6x^2 + 7xy - 3y^2 = 0\)
\(\Leftrightarrow (3x - y)(2x+3y) = 0\)
\(\Leftrightarrow \left\{ \matrix{ y = 3x \hfill \cr y = \dfrac{-2x}{3} \hfill \cr} \right.\)
+ Với \(y = 3x => 3x^2 + 9 x^2 = x + 9x\)
\(\Leftrightarrow x(6x - 5) = 0\)
=> \(x = \dfrac{5}{6} , y = \dfrac{5}{2}\) (thỏa mãn)
+ Với \(y = \dfrac{-2x}{3}\)
=> \(3x^2 + \dfrac{4x^2}{9} = x - 2x\)
\(\Leftrightarrow x(31x + 9) = 0\)
=> \(x = \dfrac{-9}{31} , y = \dfrac{6}{31}\) (thỏa mãn)
Kết luận: Tập nghiệm của hệ phương trình ...........
Câu II.
1. Đặt m = \(\overline{xy}\) ≥ 10 ta có n = 10m + z ⇒ 2(10m + z − 2) = m² − z² , từ đó biến đổi được
(m − 10)² − (z + 1)² = 95 ⇔ (m − z − 11)(m + z − 9) = 95.
Chú ý m + z − 9 > 0 và m + z − 9 > m − z − 11 nên m + z − 9 ∈ {19, 95}.
Từ đó tìm được m = 22, z = 6 (thỏa mãn), vậy n = 226
2. Sử dụng bất đẳng thức AM - GM cho hai số dương liên tiếp ta có:
\(P ≥ \dfrac{2}{(a+2b)(b+2a)} ≥ \dfrac{2.4}{(a+2b+b+2a)^2} = \dfrac{1}{18}\)
Đẳng thức xảy ra khi a = b = 2.
Vậy giá trị nhỏ nhất của P là \(\dfrac{1}{18}\)
Câu III
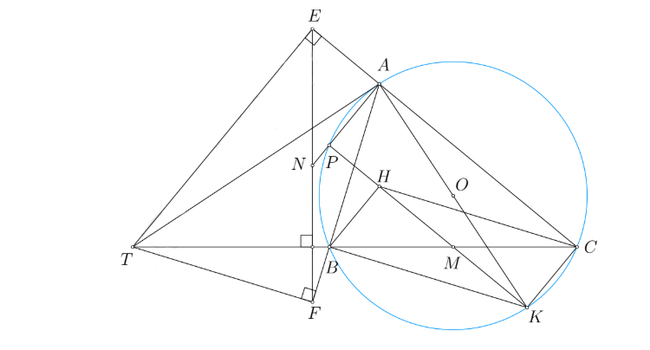
Xét các điểm có vị trí như hình vẽ, các trường hợp khác chứng minh tương tự.
1. Ta có ∠TEA = ∠TFA = 90⁰ nên TEAF là tứ giác nội tiếp, do đó
⇒ ∠TEF = ∠TAF = ∠ACB.
Bởi vậy ∠TEF + ∠ETC = ∠ACB + ∠ETC = 90⁰ ⇒ EF ⊥ BC.
2. Chú ý BH ⊥ AC, CH ⊥ AF và BC ⊥ EF, sử dụng tính chất của góc có cạnh tương ứng vuông góc ta có ∠BHC = ∠EAF, ∠EFA = ∠BCH ⇒ △BHC ∽ △EAF (g.g).
Lại có M là trung điểm BC, N là trung điểm của EF suy ra △HMC ∽ △ANF (c.g.c).
Bởi vậy ∠MHC = ∠NAF, kẻ đường kính AK của (O), khi đó tứ giác BHCK là hình bình hành nên ba điểm H, M, K thẳng hàng.
Gọi P là giao điểm của HM và AN, chú ý BK // HC ta có:
∠PKB = ∠KHC = ∠NAF = ∠PAB ⇒ P ∈ (O).
Bài toán được chứng minh.
Câu IV
Ta có đẳng thức
\(\dfrac{2\sqrt{bc}}{a + 2\sqrt{bc}} = 1 - \dfrac{a}{a + 2\sqrt{bc}}\)
Do đó biến đổi bất đẳng thức đã cho tương đương với
\(\dfrac{a}{a + 2\sqrt{bc}} + \dfrac{b}{b + 2\sqrt{ca}} + \dfrac{c}{c + 2\sqrt{ab}} ≥ 1\)
Sử dụng bất đẳng thức Cauchy - Schwarz dạng cộng mẫu ta có
\(\dfrac{a}{a + 2\sqrt{bc}} + \dfrac{b}{b + 2\sqrt{ca}} + \dfrac{c}{c + 2\sqrt{ab}} ≥ \dfrac{(\sqrt{a} + \sqrt{b} + \sqrt{c})^2}{a + b + c + 2\sqrt{ab} + 2\sqrt{bc} + 2\sqrt{ca}} = 1\)
Đẳng thức xảy ra khi a = b = c.
Từ đó bất đẳng thức ban đầu đúng, bài toán chứng minh xong.
Trên đây là đề thi thử vào lớp 10 môn Toán THPT chuyên KHTN vòng 1 - lần 2 có đáp án chi tiết, đừng quên tham khảo thêm đề thi thử vào 10 các môn khác nữa em nhé!
