Cùng Đọc tài liệu thử sức với đề thi thử tuyển sinh vào lớp 10 môn toán năm 2020 có đáp án của huyện Lục Ngạn vừa diễn ra em nhé:
Đề thi thử
Phần I TRẮC NGHIỆM (3 điểm).
Câu 1. Số nào sau đây có căn bậc hai số học bằng \(\sqrt 9\)
A. 3.
B. 9.
C. 3 và -3.
D. 81.
Câu 2. Với \(A<0; B\geq 0\), khẳng định nào đúng trong các khẳng định sau:
A. \(\sqrt{A^2B} = A\sqrt B\).
B. \(\sqrt{A^4B} = A^2\sqrt B\).
C. \(\sqrt{A^4B} = -A^2\sqrt B\).
D. \(\sqrt{A^2B} = A^2\sqrt B\).
Câu 3. Điều kiện xác định của \(\sqrt{6-3x}\) là
A. \(x \leq \dfrac{1}2\).
B. \(x \leq -2\).
C. \(x \leq 2\).
D. \(x \geq 2\).
Câu 4. Với \(0 \leq x \leq 2\), rút gọn biểu thức \(\sqrt{x^2-4x+4}+\sqrt{x^2}\) ta được
A. 2.
B. 2 - 2x.
C. 2x - 2.
D. -2.
Câu 5. Với \(x\geq -1\), giá trị của x thỏa mãn \(\sqrt{x+1}=4\) là
A. 3.
B. 5.
C. 17.
D. 15.
Câu 6. Trong các hàm sau hàm số nào là hàm số bậc nhất
A. \(y=1-\dfrac{1}x\)
B. \(y=5(x+1) - 5x \)
C. \(y=x\sqrt2+1 \)
D. \(y = \dfrac{2}3 - 2\sqrt x\)
Câu 7. Đường thẳng y = 5 - 2x không song song với đường thẳng
A. y = -2x + 1.
B. \(y=\dfrac{2}3+ \sqrt 2 ( \sqrt 2x -1)\).
C. \(y=-2x+ \sqrt 3\).
D. \(y= 6 - 2(x-5)\).
Câu 8. Với giá trị nào của tham số m thì hàm số y = 5 - 3mx là hàm số đồng biến ?
A. \(m > \dfrac{5}3\).
B. \(m> 0\).
C. \(m <0\).
D. \(m < \dfrac{5}3\).
Câu 9. Cặp số (-1;2) không là một nghiệm của phương trình
A. x + 2y = 3.
B. -x + 3y= 5.
C. 5x - y = -7.
D. x - y = -3.
Câu 10. Tung độ gốc của đường thẳng 3x - 4y = 3 là
A. \(\dfrac{-3}4\).
B. 1.
C. \(\dfrac{3}4\).
D. 3.
Câu 11. Khi hệ phương trình \(\left\{ \matrix{ mx + 3y = 1 \hfill \cr x + ny = 3 \hfill \cr} \right.\) vô nghiệm thì điều kiện của m;n là:
A. \(m.n =3;m ≠ \dfrac{1}3\).
B. \(n=9;m = \dfrac{1}3\).
C. \(m.n ≠ 3\).
D. \(m.n =3;m ≠ 3\).
Câu 12. Phương trình \(-x +\dfrac{1}2 y = 0\) có nghiệm tổng quát là
A. \(\left\{ \matrix{ x \in R \hfill \cr y =x \hfill \cr} \right.\)
B. \(\left\{ \matrix{ y \in R \hfill \cr x = 2y \hfill \cr} \right.\)
C. \(\left\{ \matrix{ x \in R \hfill \cr y =-2x \hfill \cr} \right.\)
D. \(\left\{ \matrix{ x \in R \hfill \cr y =2x \hfill \cr} \right.\)
Câu 13. Phương trình nào sau đây có tích hai nghiệm bằng 3?
A. \(x^2+x+3 = 0\)
B. \(x^2+x-3 = 0\)
C. \(x^2 -3x+1=0 \)
D. \(x^2+5x+3=0 \)
Câu 14. Cho tam giác ABC vuông tại A, có AB = 9cm, AC = 12cm. Bán kính của đường tròn ngoại tiếp tam giác ABC dài là
A. 13cm
B. 15cm
C. 7,5cm
D. 6cm
Câu 15. Cho hàm số \(y=-5x^2\), khẳng định nào dưới đây là đúng?
A. Đồ thị hàm số là một đường thẳng
B. Hàm số đồng biến khi \(x<0 \)
C. Đồ thị hàm số nằm phía trên trục hoành
D. Giá trị nhỏ nhất của hàm số là 0
Câu 16. Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn có độ dài là 2cm và 8cm. Độ dài của đường cao đó là
A. 10cm.
B. 16cm.
C. 4cm.
D. 6cm.
Câu 17. Từ điểm A bên ngoài đường tròn (O), kẻ các cát tuyến ABC và ADE với đường tròn (B nằm giữa A và C; D nằm giữa A và E). Biết ∠CAE = 45° và số đo \(\stackrel\frown{BD}= 10°\). Khi đó ∠CBE bằng
A. 50°
B. 55°
C. 40°
D. 90°
Câu 18. Cho đường tròn (O;5) và điểm A cách O một khoảng 13. Từ A kẻ tiếp tuyến AB (B là tiếp điểm) và cát tuyến ACD với đường tròn. Khi đó AC.AD bằng
A. 144.
B. 144.
C. 12.
D. 169.
Câu 19. Một cột cờ có bóng trên mặt đất dài 8m và cùng thời điểm đó tia sáng đi qua đỉnh tạo với mặt đất một góc bằng 60°. Chiều cao của cột cờ là
A. 4m
B. \(\dfrac{8\sqrt 3}3\)m
C. \(4\sqrt 3\)m
D. \(8\sqrt 3\)m
Câu 20. Giá trị của tham số m để phương trình \(x^2 - 2(m+ 5)x + 2m+ 9 = 0\) có hai nghiệm sao cho nghiệm này gấp hai lần nghiệm kia là
A. \(\dfrac {11}2\)
B. \(-\dfrac {7}2\) hoặc \(\dfrac {19}4\)
C. \(-\dfrac {7}4\)
D. \(-\dfrac {7}2\) hoặc \(-\dfrac {17}4\)
Phần II. TỰ LUẬN (7 điểm)
Câu 21.(2,0 điểm)
a) Giải hệ phương trình
\(\left\{ \matrix{ 5x + 3y = 7 \hfill \cr 2x - y = 5 \hfill \cr} \right.\)
b) Rút gọn biểu thức:
\(A = \left ( \dfrac{\sqrt x +1}{\sqrt x +2} - \dfrac{2\sqrt x}{\sqrt x - 2} - \dfrac{2x + 6\sqrt x}{4-x} \right) : \dfrac{\sqrt x - 1}{\sqrt x}\)
với \(x>0; x ≠1;x≠4\).
Câu 22.(1,0 điểm) Cho phương trình \(x^2 – 2(m-3)x+2m-7 =0 \) (1) (x là ẩn, m là tham số).
a) Giải phương trình (1) khi m = -2.
b) Tìm các giá trị của m để phương trình (1) có hai nghiệm x1,x2, thỏa mãn \(x_1\sqrt x_2 + x_2 \sqrt x_1 = 12 \)
Câu 23.(1,5 điểm) Anh Bình đến siêu thị để mua một cái Bếp ga và một cái Quạt điện với tổng số tiền theo giá niêm yết là 850 nghìn đồng. Khi thanh toán, nhân viên cho biết siêu thị đang có chương trình khuyến mãi để tri ân khách hàng sau đợt nghỉ phòng chống dịch COVID-19, cụ thể: giá của Bếp ga và Quạt điện lần lượt được giảm bớt 10% và 20% so với giá niêm yết. Do đó, anh Bình đã trả ít hơn 125 nghìn đồng so với giá niêm yết khi mua hai sản phẩm trên. Hỏi giá bán niêm yết của từng loại sản phẩm mà anh Bình đã mua là bao nhiêu?
Câu 24.(2,0 điểm) Cho hai đường tròn (O;R) và (O';r) (với \(R >r\)) tiếp xúc ngoài tại điểm I. Kẻ tiếp tuyển chung ngoài AB của hai đường tròn (A, B là các tiếp điểm, A thuộc (O); B thuộc (O')). Tiếp tuyến chung trong tại I cắt AB tại K. Kẻ đường kính AD của đường tròn (O).
a) Chứng minh tứ giác AKIO là tứ giác nội tiếp.
b) Chứng minh ba điểm B, I, D thẳng hàng.
c) Cho biết R = 9cm, r = 4cm, tính chu vi tứ giác ABO'O.
Câu 25.(0,5 điểm) Cho ba số thực không âm a, b, c và a + b + c = 3.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
\(K = \sqrt {3a+1} + \sqrt {3b+1} + \sqrt {3c+1} \).
Hết
Trên đây là tổng hợp 5 câu hỏi trong đề thi thử tuyển sinh vào lớp 10 mới nhất của huyện Lục Ngạn (Bắc Giang) với môn Toán, cùng làm bài thi này trong 120 phút rồi đối chiếu với đáp án chi tiết dưới đây em nhé:
Đáp án
Phần I. TRẮC NGHIỆM
| Câu 1 | B | Câu 11 | A |
| Câu 2 | B | Câu 12 | D |
| Câu 3 | C | Câu 13 | D |
| Câu 4 | A | Câu 14 | C |
| Câu 5 | D | Câu 15 | B |
| Câu 6 | C | Câu 16 | C |
| Câu 7 | B | Câu 17 | A |
| Câu 8 | C | Câu 18 | A & B |
| Câu 9 | B | Câu 19 | D |
| Câu 10 | A | Câu 20 | D |
Phần II. TỰ LUẬN
Câu 21
a)
\(\left\{ \matrix{ 5x + 3y = 7 \hfill \cr 2x - y = 5 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ x=2 \hfill \cr y=-1 \hfill \cr} \right.\)
b)
\(A = \left ( \dfrac{\sqrt x +1}{\sqrt x +2} - \dfrac{2\sqrt x}{\sqrt x - 2} - \dfrac{2x + 6\sqrt x}{4-x} \right) : \dfrac{\sqrt x - 1}{\sqrt x}\)
Với \(x>0; x ≠1;x≠4\), ta có:
\(A = \left ( \dfrac{\sqrt x +1}{\sqrt x +2} - \dfrac{2\sqrt x}{\sqrt x - 2} - \dfrac{2x + 6\sqrt x}{4-x} \right) : \dfrac{\sqrt x - 1}{\sqrt x}\)
\(= \dfrac{(\sqrt x +1)(\sqrt x - 2)- 2\sqrt x(\sqrt x +2)+2x + 6\sqrt x}{(\sqrt x +2)(\sqrt x - 2)} . \dfrac{\sqrt x}{\sqrt x - 1}\)
\(= \dfrac{x + \sqrt x - 2}{(\sqrt x +2)(\sqrt x - 2)} . \dfrac{\sqrt x}{\sqrt x - 1}\)
\(= \dfrac{( \sqrt x + 2)(\sqrt x - 1)}{(\sqrt x +2)(\sqrt x - 2)} . \dfrac{\sqrt x}{\sqrt x - 1} =\dfrac{\sqrt x}{\sqrt x - 2}\)
Câu 22.
a)
Với m = -2, ta có (1)
\(\Leftrightarrow x^2 – 2(-2-3)x-2.2-7 =0 \)
\(\Leftrightarrow x^2 +10 x-11=0 \)
\(\Leftrightarrow \left[ \matrix{ {x} = {1} \hfill \cr {x} = {-11} \hfill \cr} \right.\)
b)
Ta biến đổi (1)
\(\Leftrightarrow (x-1) [ x- (2m-7)] =0 \)
\(\Leftrightarrow \left[ \matrix{ {x} = {1} \hfill \cr {x} = {2m-7} \hfill \cr} \right.\)
Thay vào ta có:
\(x_1\sqrt x_2 + x_2 \sqrt x_1 = 12 \)
\(\Leftrightarrow 1\sqrt {2m-7} + (2m-7) \sqrt 1 = 12 \) (đkxđ \(m \geq \dfrac{7}2\))
\(\Leftrightarrow (2m-7) + \sqrt {2m-7} - 12 =0\)
\(\Leftrightarrow \left[ \matrix{ \sqrt {2m-7} = 3 \hfill \cr \sqrt {2m-7} = -4 \space (loại) \hfill \cr} \right.\)
\(\Leftrightarrow m = 8\) (thoả mãn đkxđ)
KL.....
Câu 23.
Gọi giá bán niêm yết của Bếp và Quạt mà anh Bình đã mua lần lượt là A và B (Nghìn đồng, \(A;B > 0\))
Theo bài ra ta có hệ:
\(\left\{ \matrix{ A+B =850 \hfill \cr A.0,9 + B. 0,8 = 850 -125 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ A = 450 \hfill \cr B = 400 \hfill \cr} \right.\) (nghìn đồng)
KL....
Câu 24.
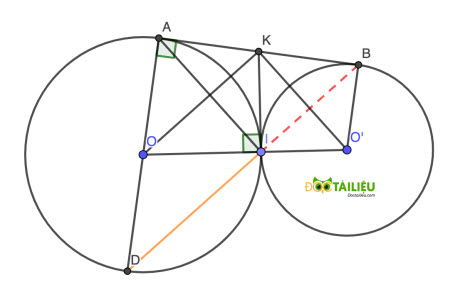
a)
Vì AB là tiếp tuyến của (O) tại A ⇒ AB ⊥ OA
Vì IK là tiếp tuyến của (O) tại I ⇒ IK ⊥ OI
Suy ra ∠KIO = ∠KAO = 90° ⇒ I, A cùng thuộc đường tròn đường kính OK, hay tứ giác AKIO nội tiếp (đpcm).
b)
Xét △IAD nội tiếp (O) có AD là đường kính ⇒ ∠AID = 90° ⇒ AI ⊥ ID (1).
Ta thấy KA và KI là tiếp tuyến từ K tới (O) ⇒ KA = KI
Tương tự KI và KB là tiếp tuyến từ K tới (O') ⇒ KI = KB = KA ⇒ △IAB vuông tại I (theo tính chất tam giác vuông có đường trung tuyến bằng một nửa cạnh huyền) ⇒ AI ⊥ IB (2)
Từ (1) và (2) ⇒ I, D, B thẳng hàng (đpcm)
c)
Vì tứ giác AKIO nội tiếp ⇒ ∠OKI = ∠OAI = ∠OIA
Tương tự dễ chứng minh BKIO' nội tiếp ⇒ ∠O'KI = ∠O'BI = ∠O'IB
Cộng vế theo vế hai biểu thức trên, có:
∠OKO' = ∠OKI + ∠O'KI = ∠OIA + ∠O'IB = 90° - ∠AIK + 90° - ∠KIB = 180° - ∠AIB = 90°.
Áp dụng hệ thức lượng trong △OKO' vuông tại K, đường cao KI, ta có:
\(KI² = IO.IO' = R.r \Rightarrow KI = \sqrt {9.4}=6\) (cm)
Ta có chu vi tứ giác ABO'O là:
P = AB + BO' + O'I + IO + OA = 2KI + 2r + 2R = 2.6 + 2.4 + 2.9 = 38 (cm).
KL........
Câu 25.
Áp dụng BĐT Bunhya-Copxki, ta có:
\(K^2 = (1.\sqrt {3a+1} + 1.\sqrt {3b+1} + 1.\sqrt {3c+1} )^2 \leq (1+1+1)(3a+1+3b+1+3c+1)\)
\(\Leftrightarrow K^2 \leq 3[3+ 3(a+b+c)] = 3.(3+3.3) = 36\)
\(\Leftrightarrow K \leq 6\).
Vậy \({Max}_K = 6 \Leftrightarrow a=b=c =1 \).
Không mất tính tổng quát, giả sử \(c = max\{a;b;c\}\)
Ta đi chứng minh \(K \geq 2+\sqrt {10}\)
\(\Leftrightarrow \sqrt {3a+1} -1 + \sqrt {3b+1} -1 + \sqrt {3c+1} - \sqrt {10} \geq 0\)
\(\Leftrightarrow \dfrac{3a}{\sqrt {3a+1} +1} + \dfrac{3b}{\sqrt {3b+1} +1} + \dfrac{3(c-3)}{\sqrt {3c+1} +\sqrt {10} } \geq 0\)
\(\Leftrightarrow \dfrac{3a}{\sqrt {3a+1} +1} + \dfrac{3b}{\sqrt {3b+1} +1} - \dfrac{3(a+b)}{\sqrt {3c+1} +\sqrt {10} } \geq 0\) (thay a + b = 3 - c vào)
\(\Leftrightarrow 3a\left(\dfrac{1}{\sqrt {3a+1} +1} - \dfrac{1}{\sqrt {3c+1} +\sqrt {10} } \right) + 3b\left(\dfrac{1}{\sqrt {3b+1} +1} - \dfrac{1}{\sqrt {3c+1} +\sqrt {10} } \right) \geq 0\)
(1)Vì \(c = max\{a;b;c\}\)suy ra:
\(\left\{ \matrix{ \sqrt {3a+1} \leq \sqrt {3c+1} \hfill \cr \sqrt {3b+1} \leq \sqrt {3c+1} \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ \sqrt {3a+1} + 1<\sqrt {3c+1} +\sqrt{10} \hfill \cr \sqrt {3b+1} +1<\sqrt {3c+1} +\sqrt{10} \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ \dfrac{1}{\sqrt {3a+1} + 1}> \dfrac{1}{\sqrt {3c+1} +\sqrt{10}} \hfill \cr \dfrac{1}{\sqrt {3b+1} + 1}> \dfrac{1}{\sqrt {3c+1} +\sqrt{10}} \hfill \cr} \right.\)
⇒ (1) luôn đúng, mà các phép biến đổi là tương đương hay \(K \geq 2+\sqrt {10}\) là đúng.
Vậy \({Min}_K = 2+\sqrt{10} \Leftrightarrow a=b=0;c= 3 \) và các hoán vị.
-/-
Trên đây là hướng dẫn giải chi tiết đề thi thử vào 10 môn toán năm 2020 huyện Lục Ngạn (Bắc Giang), mong rằng đây sẽ là tài liệu hữu ích giúp các em ôn tập. Đừng quên còn rất nhiều tài liêu đề thi thử vào lớp 10 môn toán 2020 khác của các tỉnh thành trên cả nước nhé.
