Cùng Đọc tài liệu thử sức với đề thi thử vào lớp 10 môn toán năm học 2021 - 2022 trường Thanh Xuân Trung lần thứ nhất vừa ra em nhé:
Đề thi thử
|
PHÒNG GD-ĐT QUẬN THANH XUÂN TRƯỜNG THCS THANH XUÂN TRUNG |
ĐỀ THI THỬ VÀO LỚP 10 2021 Thời gian làm bài : 120 phút |
Bài 1: (2 điểm)
Cho các biểu thức \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2+5 \sqrt{x}}{4-x}\) và \(B=\dfrac{2 \sqrt{x}}{\sqrt{x}+2}\)a) Tính giá trị biểu thức B khi \(x^2 = 4\)
b) Rút gọn biểu thức P = B + A
c) So sánh √P với 2.
Bài 2: (2 điểm) Năm học 2020 - 2021, một trường THCS có 3 lớp 9 gồm 9A, 9B, 9C trong đó lớp 9A có 35 học sinh và lớp 9B có 40 học sinh. Tổng kết cuối năm học, lớp 9A có 15 học sinh giỏi, lớp 9B có 12 học sinh giỏi, lớp 9C có 20% học sinh đạt học sinh giỏi và toàn khối 9 có 30% học sinh đạt học sinh giỏi. Hỏi lớp 9C có bao nhiêu học sinh.
Bài 3: (2 điểm)
1. Giải hệ phương trình
\(\left\{\begin{array}{l} 2|x-1|-\dfrac{1}{y^{2}+2}=4 \\ |x-1|+\dfrac{3}{y^{2}+2}=\dfrac{15}{4} \end{array}\right.\)
2. Cho phương trình: \(x^2 – (m – 1)x – m = 0 \)
a) Giải phương trình với m = 4
b) Tìm m để phương trình có 2 nghiệm phân biệt \(x_1, x_2 \)thỏa mãn điều kiện
\(x_1(3 – x_2) + 20 ≥ 3(3 – x_2)\)
Bài 4: (3,5 điểm)
Cho (O;R) đường kính AB.Từ điểm C bất kỳ trên (O) vẽ CH ⊥ AB (H∈AB). Gọi M, N lần lượt là hình chiếu của H trên CA, CB.
a) Chứng minh: Tứ giác CMHN là hình chữ nhật.
Giả sử R = 3cm, AH = 1,5cm. Tính MN.
b) Chứng minh: Tứ giác AMNB nội tiếp.
c) MN cắt AB tại E. CE cắt (O) tại Q. Chứng minh CQ ⊥ QH
d) Gọi P là tâm đường tròn ngoại tiếp tứ giác AMNB. Gọi F đối xứng với C qua O. Chứng minh H, P, F thẳng hàng
Bài 5: (0,5 điểm)
Cho a, b, c > 0 và a + b + c = 1.
Tìm giá trị lớn nhất của biểu thức \(A = \dfrac{{ab}}{{\sqrt {c + ab} }} + \dfrac{{bc}}{{\sqrt {a + bc} }} + \dfrac{{ca}}{{\sqrt {b + ca} }}\)
Hết
Vậy là cấu trúc đề thi thử vào lớp 10 môn Toán của trường THCS Thanh Xuân Trung đều không có nhiều thay đổi so với cấu trúc đề tuyển sinh vào lớp 10 các năm. Hãy thử sức làm bài trong thời gian 120 phút rồi so sánh đối chiếu với lời giải chi tiết dưới đây sau em nhé.
Đáp án đề thi thử vào lớp 10 môn Toán năm 2021
Bài 1: (2 điểm)
a) ĐKXĐ: x ≥ 0, ta có: \( x^2 = 4 \Leftrightarrow x = 2\)
Ta có:
\(B=\dfrac{2 \sqrt{x}}{\sqrt{x}+2} =\dfrac{2 \sqrt{2}}{\sqrt{2}+2} =\dfrac{2}{\sqrt{2}+1}\)
b) Rút gọn biểu thức P = B + A
ĐKXĐ: x ≥ 0; x ≠ 4 ta có:
\(P=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2+5 \sqrt{x}}{4-x} + \dfrac{2 \sqrt{x}}{\sqrt{x}+2}\)
\(=\dfrac{(\sqrt{x}+1)(\sqrt{x}+2) - (2+5 \sqrt{x}) + 2 \sqrt{x} (\sqrt{x}-2)}{(\sqrt{x}-2)(\sqrt{x}+2)} \)
\(=\dfrac{x + 3\sqrt{x}+2 - 2-5 \sqrt{x}+ 2 x -4\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)} \)
\(=\dfrac{3x - 6\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)} \) \(=\dfrac{3\sqrt{x}(\sqrt{x}-2)}{(\sqrt{x}-2)(\sqrt{x}+2)} \)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}+2} \)
c) Dễ thấy P ≥ 0 với mọi x thỏa đkxđ.
Ta có:
\(P - 4 =\dfrac{3\sqrt{x}}{\sqrt{x}+2}-4 \)
\(=\dfrac{3\sqrt{x}-4(\sqrt{x}+2)}{\sqrt{x}+2} \)
\(=\dfrac{-8-\sqrt{x}}{\sqrt{x}+2} < 0 \) với mọi x thỏa đkxđ
Hay \(P - 4 < 0 \Leftrightarrow P < 4 \Leftrightarrow \sqrt{P} <2 \) (vì P ≥ 0).
KL...
Bài 2: (2 điểm)
Gọi số học sinh lớp 9C có là A (A ∈ ℕ)
Số học sinh giỏi lớp 9C là: 20% A = 0,2A (học sinh)
Số học sinh giỏi toàn khối là: 30%(35 + 40 + A) = 15 + 12 + 0,2A
⇔ 0,3 (75 + A) = 27 + 0,2 A
⇔ 0,1 A = 4,5 ⇔ A = 45 (học sinh)
KL...
Bài 3: (2 điểm)
1.
\(\left\{\begin{array}{l} 2|x-1|-\dfrac{1}{y^{2}+2}=4 \\ |x-1|+\dfrac{3}{y^{2}+2}=\dfrac{15}{4} \end{array}\right.\)
\(⇔ \left\{\begin{array}{l} |x-1|=\dfrac{9}{4} \\ \dfrac{1}{y^{2}+2}=\dfrac{1}{2} \end{array}\right.\)
\(⇔ \left\{\begin{array}{l} \left[ \matrix{ x = \dfrac{13}{4} \hfill \cr x = \dfrac{-5}{4} \hfill \cr} \right. \\ y = 0 \end{array}\right.\)
KL...
2. Cho phương trình: \(x^2 – (m – 1)x – m = 0 \)
a) Với m = 4 ta có:
\(x^2 – 3x – 4 = 0 \)
\(\Leftrightarrow \left[ \matrix{ x = -1 \hfill \cr x = 4 \hfill \cr} \right. \)
KL...
b) Để phương trình có 2 nghiệm phân biệt ⇔
\(\Delta = (m-1)^2 + 4m = (m+1)^2 > 0\)⇔ m ≠ -1.
Áp dụng hệ thức Vi-ét ta có:
\(\left\{ \matrix{ x_1+x_2 = m-1 \hfill \cr x_1x_2 = -m \hfill \cr} \right.\)
Ta có:
\(x_1(3 – x_2) + 20 ≥ 3(3 – x_2)\)
\(\Leftrightarrow 3(x_1+x_2) - x_1x_2 + 11 ≥ 0\)
\(\Leftrightarrow 3(m-1) +m + 11 ≥ 0\)
\(\Leftrightarrow 4m + 8 ≥ 0\)
\(\Leftrightarrow m ≥ -2\)
KL: m ≥ -2 và m ≠ -1.
Bài 4: (3,5 điểm)
Ta có hình vẽ:
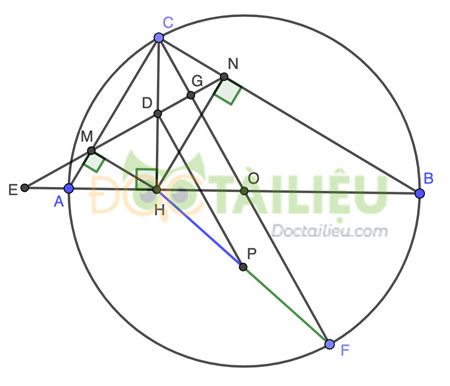
a)
Vì C thuộc đường tròn đường kính AB ⇒ ∠ACB = 90° = ∠MCN
Lại có M, N là hình chiếu của H trên CA, CB ⇒ ∠CMH = ∠CNH = 90° = ∠MCN ⇒ Tứ giác CMHN là hình chữ nhật (đpcm).
Áp dụng hệ thức lượng trong tam giác vuông ACB ta có:
CH² = AH.HB = AH.(AB - AH) = AH.(2R - AH)
= 1,5 (2.3 - 1,5) = 6,75
⇒ \(CH = \dfrac{3\sqrt3}2\) (cm)
Vì CMHN là hình chữ nhật ⇒ \(MN = CH = \dfrac{3\sqrt3}2 \) (cm).
b)
Ta có ∠MAB = ∠CAH = ∠CHM = ∠CNM (CMHN là hình chữ nhật) = 180° - ∠MNB
⇒ ∠MAB + ∠MNB = 180° ⇒ Tứ giác AMNB nội tiếp (đpcm).
c)
Xét △EMA và △EBN ta có:
∠EMA = 180 - ∠AMN = ∠EBN (do tứ giác AMNB nội tiếp - cmt)
Góc ∠BEN chung
Suy ra △EMA ∽ △EBN (g.g) ⇒ \(\dfrac{EM}{EB} = \dfrac{EA}{EN}\) ⇒ EM.EN = EA.EB (1)
Tương tự ta có tứ giác AQCB nội tiếp ⇒ △EQA ∽ △EBC (g.g) ⇒ EQ.EC = EA.EB (2)
Từ (1) và (2) ⇒ EQ.EC = EM.EN ⇒ \(\dfrac{EQ}{EM} = \dfrac{EN}{EC}\).
Xét △EQM và △ENC ta có:
\(\dfrac{EQ}{EM} = \dfrac{EN}{EC}\) (cmt)
Góc ∠CEN chung
Suy ra △EQM ∽ △ENC (c.g.c) ⇒ ∠EQM = ∠ENC ⇒ Tứ giác QMNC nội tiếp
hay 5 điểm C, Q, M, H, N cùng thuộc đường tròn đường kính CH ⇒ ∠CQH = ∠CMH = 90°
Hay CQ ⊥ QH (đpcm).
d)
Gọi MN cắt CH tại D, CF cắt MN tại G.
Ta thấy ∠CQF = 90° = ∠CQH (cmt) ⇒ Q, H, F thẳng hàng
Gọi P' là trung điểm HF. Dễ thấy theo tính chất đường trung bình trong △HCF ta có:
P'O // CH
Và P'D // CF.
mà CH ⊥ AB ⇒ P'O ⊥ AB, mà O là trung điểm AB ⇒ P'O là trung trực của AB ⇒ P'A = P'B (3)
Lại có ∠GCN + ∠GNC = ∠OCB + ∠MNC = ∠OBC + ∠MAB = ∠ABC + ∠CAB = 90°
⇒ ∠CGN = 90° ⇒ CF ⊥ MN
⇒ P'D ⊥ MN, lại có D là trung điểm MN ⇒ P'D là trung trực của MN ⇒ P'M = P'N (4)
Từ (3) và (4) kết hợp với tứ giác AMNB nội tiếp (cmt) ⇒ P' là tâm đường tròn ngoại tiếp AMNB
Hay P' ≡ P hay ba điểm H, P, F thẳng hàng (đpcm).
Bài 5: (0,5 điểm)
Áp dụng BDT AM-GM ta có:
\( \dfrac{ab}{\sqrt {c + ab} } = \dfrac{ab}{\sqrt {c(a+b+c) + ab} } \)
\(= \dfrac{ab}{\sqrt {(c+a)(c+b)} } \leq \dfrac{ab}{2}\left( \dfrac{1}{c+a} + \dfrac{1}{c+b}\right)\)
Chứng minh tương tự ta có:
\( \dfrac{bc}{\sqrt {a + bc} } \leq \dfrac{bc}{2}\left( \dfrac{1}{a+b} + \dfrac{1}{a+c}\right)\)
và \( \dfrac{ca}{\sqrt {b + ca} } \leq \dfrac{ca}{2}\left( \dfrac{1}{b+a} + \dfrac{1}{b+c}\right)\)
Cộng vế theo vế 3 BDT trên ta có:
\(A \leq \dfrac{1}2 \left[ \dfrac{b}{a+c}(a+c) + \dfrac{c}{a+b}(a+b) +\dfrac{a}{b+c}(b+c)\right]\)
\(⇔ A \leq \dfrac{1}2 (a+b+c) = \dfrac{1}2\)
Vậy \({Max}_A = \dfrac{1}2 \Leftrightarrow a=b=c = \dfrac{1}3\).
Trên đây là hướng dẫn giải chi tiết đề thi thử vào 10 môn toán năm 2021 lần 1 của THCS Thanh Xuân Trung, mong rằng đây sẽ là tài liệu hữu ích giúp các em ôn tập. Đừng quên còn rất nhiều tài liêu đề thi thử tuyển sinh vào lớp 10 môn toán khác của các tỉnh thành trên cả nước nhé.
