Cùng Đọc tài liệu thử sức với đề thi thử vào lớp 10 môn toán năm học 2021 - 2022 trường Lương Thế Vinh lần thứ nhất vừa ra em nhé:
Đề thi thử
|
TRƯỜNG THCS & THPT LƯƠNG THẾ VINH |
ĐỀ THI THỬ VÀO LỚP 10 Năm học: 2021 – 2022 MÔN: TOÁN - Lần thứ nhất Thời gian làm bài: 120 phút |
Bài 1. (2,0 điểm)
Cho các biểu thức \(A=\dfrac{\sqrt{x}-4}{\sqrt{x}-8}+\dfrac{5}{\sqrt{x}+8}+\dfrac{\sqrt{x}-72}{64-x}\) và \(B=\dfrac{\sqrt{x}-8}{2 \sqrt{x}-1}\) với \(x \geq 0 ; x \neq 64 ; x \neq \dfrac{1}{4}\)
a) Tính giá trị của biểu thức B khi x=25
b) Rút gọn biểu thức A
c) Đặt T = A.B. Tim các số nguyên dương x để \(|T|>\dfrac{3}{5}\).
Bài 2 (2,5 điểm)
Theo kế hoạch, hai công ty chế biến nông sản sẽ xuất khẩu tổng số 150 tấn vải thiều. Nhưng do dịch bệnh Covid 19 nên khối lượng xuất khẩu vải thiều của công ty thứ nhất giảm 30%, công ty thứ hai giảm 40%. Vì vậy, cả hai công ty chỉ xuất khẩu được 95 tấn. Hỏi theo kế hoạch, mỗi công ty xuất khẩu bao nhiêu tấn vải thiều?
khấu bao nhiêu tấn vải thiều?
2) Một cột cờ cao 12m có bóng trên mặt đất dài 9m. Gần đó có một cái cây, tại thời điểm đó có bóng dài 6m thì chiều cao của cây đó là bao nhiêu?
Bài 3 (2 điểm):
1) Giải hệ phương trình: \(\left\{\begin{array}{l}\dfrac{3}{2 x+1}+\dfrac{1}{|y-3|}=2 \\ \dfrac{1}{2 x+1}+\dfrac{4}{|y-3|}=\dfrac{5}{2}\end{array}\right.\)
2) Cho hai đường thẳng \(y=(m+1) x+2 m\left(d_{1}\right)\) và \(y=2 x+4\left(d_{2}\right)\)
a) Tìm m để đường thẳng (d1) song song với đường thẳng (d2).
b) Với giá trị của m tìm được ở câu trên, hãy tính khoảng cách giữa hai đường thẳng.
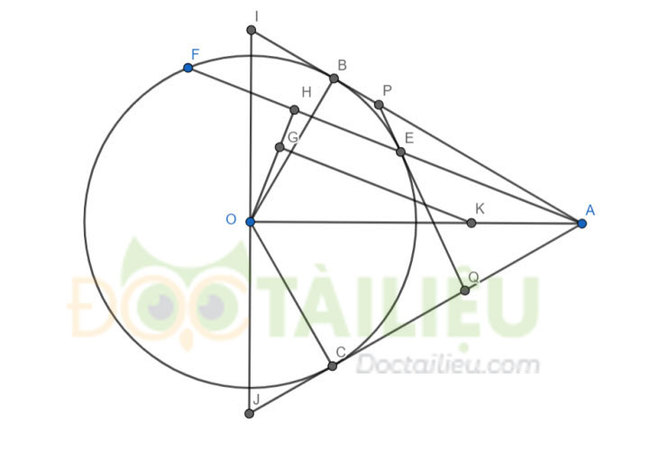
Bài 4 (3 điểm) Cho đường tròn (O;R) và điểm A nằm ngoài đường tròn sao cho OA =2R. Vẽ các tiếp tuyến AB, AC của (O;R) (B, C là các tiếp điểm) và qua A vẽ đường thẳng d cắt (O;R) tại hai điểm phân biệt E, F (E nằm giữa A và F). Gọi H là trung điểm của EF.
a) Chứng minh năm điểm A, B, C, H, O cùng thuộc một đường tròn.
b) Qua (O) vẽ đường thẳng vuông góc với OA tại O, đường thằng này cắt AB, AC lần lượt tại I, J. Tiếp tuyến tại E của (O) cắt AB, AC lần lượt tại P và Q. Tính diện tích tam giác AIJ và chu vi tam giác APQ.
c) Khi đường thẳng d thay đổi nhưng vẫn cắt (O) tại hai điểm E, F thì trọng tâm G của tam giác OEF chạy trên đường nào?
Bài 5, (0,5 điểm) Cho x, y là các số thực dương thỏa mãn x + y = 20.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P=3 \sqrt{x-4}+5 \sqrt{y-6}\)
- Hết -
Vậy là cấu trúc đề thi thử vào lớp 10 môn Toán của trường Lương Thế Vinh năm 2021 lần thứ nhất đều không có nhiều thay đổi so với cấu trúc đề tuyển sinh vào lớp 10 các năm. Hãy thử sức làm bài trong thời gian 120 phút rồi so sánh đối chiếu với lời giải chi tiết dưới đây sau em nhé.
Đáp án đề thi thử vào 10 môn Toán Lương Thế Vinh lần 1
Bài 1.
a) Với x = 25 (thỏa ĐKXĐ) ta có:
\(B=\dfrac{\sqrt{25}-8}{2 \sqrt{25}-1} = \dfrac{-3}{2.5-1} = \dfrac{-1}3\)
b) Với \(x \geq 0 ; x \neq 64 ; x \neq \dfrac{1}{4}\), ta có:
\(A=\dfrac{\sqrt{x}-4}{\sqrt{x}-8}+\dfrac{5}{\sqrt{x}+8}+\dfrac{\sqrt{x}-72}{64-x}\)
\(=\dfrac{(\sqrt{x}-4)(\sqrt{x}+8)+5(\sqrt{x}-8)+72 -\sqrt{x} }{(\sqrt{x}-8)(\sqrt{x}+8)}\)
\(=\dfrac{x + 4\sqrt{x} - 32 +5\sqrt{x}-40+72 -\sqrt{x} }{(\sqrt{x}-8)(\sqrt{x}+8)}\)
\(=\dfrac{x + 8\sqrt{x} }{(\sqrt{x}-8)(\sqrt{x}+8)}\) \(=\dfrac{\sqrt{x} }{\sqrt{x}-8}\)
c) Với \(x \geq 0 ; x \neq 64 ; x \neq \dfrac{1}{4}\), ta có:
T = A.B
\(=\dfrac{\sqrt{x} }{\sqrt{x}-8}.\dfrac{\sqrt{x}-8}{2 \sqrt{x}-1}\)
\(=\dfrac{\sqrt{x} }{2 \sqrt{x}-1}\)Để \(|T|>\dfrac{3}{5} \Leftrightarrow T^2 > \dfrac{9}{25}\)
\(\Leftrightarrow \left(\dfrac{\sqrt{x} }{2 \sqrt{x}-1}\right)^2 > \dfrac{9}{25}\)
\(\Leftrightarrow \dfrac{x}{(2 \sqrt{x} -1)^2} - \dfrac{9}{25} > 0\)
\(\Leftrightarrow \dfrac{25x- 9 (4x - 4 \sqrt{x} + 1)}{25(2 \sqrt{x} -1)^2} > 0\)
\(\Leftrightarrow \dfrac{-11x +36 \sqrt{x} -9}{25(2 \sqrt{x} -1)^2} > 0\)
\(\Leftrightarrow {-11x +36 \sqrt{x} -9} > 0\)
\(\Leftrightarrow( \sqrt{x} -3)(3-11\sqrt{x}) > 0\)
\(\Leftrightarrow \dfrac{3}{11} < \sqrt{x} < 3\)
\(\Leftrightarrow \dfrac{9}{121} < {x} < 9\)
Kết hợp với ĐKXĐ suy ra \( \dfrac{9}{121} < {x} < 9\) và \(x \neq \dfrac{1}{4}\).
KL...
Bài 2
a.
Gọi số vải thiều theo dự kiến của công ty 1 là x tấn \((x>0, x \in \mathbf{R})\), thì số vải thiều của công ty 2 là 150 - x( tấn ). Do khối lượng vải của công ty 1 bị giảm 30 %, công ty 2 bị giảm 40 % nên tổng sản lượng vải của cả hai công ty là: \(x .0,7+(160-x) \cdot 0,6\)
Suy ra:
\(0,7 . x+0,6 .(150-x)=96 \Leftrightarrow 0,1 . x=6 \Leftrightarrow x=60\)
Vậy số vải dự kiến của công ty 1 là 60 tấn, của công ty 2 là 90 tấn.
b.
Gọi chiều cao của cây là \(x (m; x>0, x \in \mathbf{R})\). Vì góc chiếu của tia nắng là như nhau nên tam giác tạo bởi cột cờ và bóng và tam giác tạo bởi cây và bóng là hai tam giác đồng dạng. Do đó, ta có:
\(\dfrac{x}{12}=\dfrac{6}{9} \Leftrightarrow x=12 \cdot \dfrac{6}{9} \Leftrightarrow x=8\)
Vậy cây có độ cao 8 m.
Bài 3
1) ĐKXĐ: \(x \neq \dfrac{-1}{2}\) và \(y \neq 3\), ta có:
\(\left\{\begin{array}{l}\dfrac{3}{2 x+1}+\dfrac{1}{|y-3|}=2 \\ \dfrac{1}{2 x+1}+\dfrac{4}{|y-3|}=\dfrac{5}{2}\end{array}\right.\)
\(\Leftrightarrow \left\{\begin{array}{l}\dfrac{1}{2 x+1}=\dfrac{1}2 \\ \dfrac{1}{|y-3|}=\dfrac{1}{2}\end{array}\right.\)
\(\Leftrightarrow \left\{\begin{array}{l} 2x + 1 = 2 \\ |y-3| = 2 \end{array}\right.\)
\(\Leftrightarrow \left\{\begin{array}{l} x = \dfrac{1}2 \\ \left[ \matrix{ y = 5 \hfill \cr y = 1 \hfill \cr} \right. \end{array}\right.\)
(thỏa mãn đkxđ)KL...
2)
a) Để (d1) song song với (d2), ta có:
\(\left\{ \matrix{ m+1 = 2 \hfill \cr 2m \neq 4 \hfill \cr} \right.\) \(\Leftrightarrow m = 1\)
KL...
b) Ta có:
(d1): y = 2x + 2
(d2): y = 2x + 4
Gọi điểm M(0;2) là 1 điểm thuộc đường thẳng (d1). Ta thấy khoảng cách của 2 đường thẳng song song (d1) và (d2) chính là khoảng cách từ điểm M(0;2) ∈ (d1) tới (d2).
Ta có:
\(d = d(M;d1) = \dfrac{2.0 - 2 + 4}{\sqrt{2^2 + 1}} = \dfrac{2}{\sqrt{5}} \)
KL...
Bài 4
a. Vì H là trung điểm của EF nên \(OH \perp E F,\, ∠OHA=90^{\circ} \).Suy ra, H nằm trên đường tròn đường kính OA (1).
Vì AB, AC là tiếp tuyến của đường tròn tâm O nên ∠OBA = ∠OCA = 90⁰. Suy ra B, C cũng nằm trên đường tròn đường kính OA (2).
Từ (1) và (2) suy ra, H, B, C cùng nằm trên đường tròn đường kính OA, hay A, B, C, H, O cùng nằm trên một đường tròn. -> đpcm
b. Xét △IOA vuông tại O, có đường cao OB. Áp dụng hệ thức lượng, ta được: \(O A^{2}=A B \cdot A I \Leftrightarrow A I=\dfrac{O A^{2}}{A B}\)
Lại có: \(O A=2 R, A B=\sqrt{O A^{2}-O B^{2}}=R \sqrt{3}\)
Suy ra: \(A I=\dfrac{O A^{2}}{A B}=\dfrac{4 R^{2}}{R \sqrt{3}}=R \dfrac{4}{\sqrt{3}}\)
Xét △OAI vuông tại O, có \(O A^{2}+O I^{2}=A I^{2} \Rightarrow O I=\sqrt{A I^{2}-O A^{2}}=R \dfrac{2}{\sqrt{3}} \)
Suy ra, \(I J=2 O I=R \dfrac{4}{\sqrt{3}}\)
Vậy, chu vi tam giác AIJ là \(P_{A I J}=A I+A J+I J=R \dfrac{12}{\sqrt{3}}=4 \sqrt{3} R\).
Vì EP, BP là tiếp tuyến của đường tròn tâm O nên EP = BP ; vì CQ, EQ là tiếp tuyến của đường tròn tâm O nên EQ = CQ.
Suy ra, chu vi tam giác APQ bằng
\(P_{APQ}\) = AP + AQ + PQ = AP + PE + EQ + AQ =AP + PS + AQ + QC = AB + AC = 2AB (do AB, AC là hai tiếp tuyến của đường tròn tâm O nên AB = AC).
Lại có \(A B=\sqrt{O A^{2}-O B^{2}}=R \sqrt{3}\). Suy ra, chu vi tam giác APQ là \(P_{A P Q}=2 A B=2 \sqrt{3} R\).
c. Do G là trọng tâm của tam giác OEF nên \(O G=\dfrac{2}{3} O H\).
Trên đoạn thẳng OA, lấy điểm K sao cho \({OK}=\dfrac{2}{3} OA\).Vi A, O cố định nên K cố định. Vì \( \dfrac{O A}{O K}=\dfrac{O H}{O G}\)nên \(G K \| A H \Rightarrow ∠OGK=90^{\circ}\)
Suy ra, G nằm trên đường tròn đường kính OK. Khi đường thằng D di chuyển, G sẽ di chuyển trên đường tròn đường kính OK cố định.
Bài 5. Cho x, y là các số thực dương thỏa mãn x + y = 20.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P=3 \sqrt{x-4}+5 \sqrt{y-6}\)
ĐKXĐ \(x \geq 4 \) và \(y \geq 6\).
Áp dụng Bất đẳng thức Bunhiacopxki, ta có:
\(P^2 =(3 \sqrt{x-4}+5 \sqrt{y-6})^2 \leq (3^2 + 5^2)(x-4+y-6)\)
\(\Leftrightarrow P^2 \leq 34(x+y-10) = 34.(20-10) = 340\)
\(\Leftrightarrow P \leq \sqrt{340} = 2\sqrt{85}\)
Vậy \({Max}_P = 2\sqrt{85}\) \(\Leftrightarrow \left\{ \matrix{ x+y = 20 \hfill \cr \dfrac{x-4}{9}=\dfrac{y-6}{25} \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ x = \dfrac{113}{17} \hfill \cr y=\dfrac{227}{17} \hfill \cr} \right.\).
Đặt x - 4 = a ⇔ x = a + 4
Ta có: x + y = 20 ⇔ y - 6 = 14 - x = 10 - a
Đặt \(t =\sqrt{a}+ \sqrt{10-a}\)
\(⇒ t^2 =(\sqrt{a}+ \sqrt{10-a})^2 = 10 + 2\sqrt{a(10-a)} \geq 10\)
\(⇔ t \geq \sqrt{10}\)
Ta có:
\(P =3 \sqrt{a}+5 \sqrt{10-a}\)
\(=3 t+2 \sqrt{10-a} \geq 3\sqrt{10} + 0\)
\(⇔ P \geq 3\sqrt{10}\)
Vậy \({Min}_P = 3\sqrt{10}\) \(\Leftrightarrow \left\{ \matrix{ \sqrt{a(10-a)}=0 \hfill \cr \sqrt{10-a}=0 \hfill \cr} \right.\) \(\Leftrightarrow a = 10\) \(\Leftrightarrow \left\{ \matrix{ x = 14 \hfill \cr y = 6 \hfill \cr} \right.\)
KL....
Trên đây là hướng dẫn giải chi tiết đề thi thử vào 10 môn toán năm 2021 trường Lương Thế Vinh lần 1, mong rằng đây sẽ là tài liệu hữu ích giúp các em ôn tập. Đừng quên còn rất nhiều tài liêu đề thi thử vào 10 môn toán khác của các tỉnh thành trên cả nước nhé.
