Huyện Lý Nhân (Hà Nam) vừa tổ chức kỳ thi thử tuyển sinh vào lớp 10 dành cho các em học sinh khối lớp 9, cùng Đọc tài liệu tham khảo để thi thử tuyển sinh vào lớp 10 môn Toán diễn ra vào sáng ngày 6/7/2020 em nhé:
Đề thi
Câu 1. (2,0 điểm)
1) Tính:
\(A = \sqrt{12} + 3\sqrt{\dfrac{1}3} - \sqrt{4-2\sqrt3}\)
2) Cho biểu thức:
\(B = \left(\dfrac{1}{x-\sqrt x} + \dfrac{1}{\sqrt x -1} \right): \dfrac{\sqrt x+1}{(\sqrt x -1)^2}\)
Với \(x > 0; x ≠ 1\)
a) Rút gọn biểu thức B.
b) Tìm giá trị của x để \(B = \dfrac{1}3\).
Câu 2. (1,5 điểm)
a) Giải phương trình:
\(4x^4 + x^2 - 3 = 0\)
b) Giải hệ phương trình:
\(\left\{ \matrix{ \dfrac{3}2x - y = 1 \hfill \cr -5x + 4y = -3 \hfill \cr} \right.\)
Câu 3. (2,0 điểm)
Trong mặt phẳng toạ độ Oxy cho (P): \(y = \dfrac{1}2 x^2\)
a) Điểm \(H(-1;-\dfrac{1}2)\) có thuộc đồ thị hàm số (P) không? Vì sao?
b) Tìm các điểm thuộc đồ thị hàm số (P) có tung độ bằng 8?
c) Đường thẳng (d) đi qua M(0;2) và không trùng với Oy. Chứng minh rằng (d) cắt (P) tại 2 điểm phân biết A, B sao cho △AOB vuông tại O.
Câu 4. (3,5 điểm)
Cho đường tròn (O) và điểm M nằm ngoài đường tròn. Từ M vẽ cát tuyến MCD không đi qua tâm O và hai tiếp tuyến MA và MB đến đường tròn (O) (A, B là các tiếp điểm và C nằm giữa M, D). Gọi I là trung điểm của CD.
a) Chứng minh rằng: Bốn điểm M, I, O, B cùng thuộc một đường tròn.
b) Chứng minh rằng: MA² = MC.MD.
c) Gọi H là giao điểm của AB và MO. Chứng minh tức giác CHOD nội tiếp được đường tròn. Suy ra HA là tia phân giác của góc CHD.
d) Gọi K là giao điểm của các tiếp tuyến tại C và D của đường tròn (O). Chứng minh: 3 điểm A, B, K thẳng hàng.
Câu 5. (1,0 điểm)
Cho ba số dương x, y, z thoả mãn: x + y + z = 1. Chứng minh rằng:
\(\sqrt{2x^2 + xy + 2y^2}+ \sqrt{2y^2 + yz + 2z^2}+ \sqrt{2z^2 + zx + 2x^2} \geq \sqrt 5\)
Xem thêm các tài liệu đề thi thử tuyển sinh vào lớp 10 tất cả các môn ăm 2020 nữa em nhé!
Đáp án
Câu 1.
1)
\(A = \sqrt{12} + 3\sqrt{\dfrac{1}3} - \sqrt{4-2\sqrt3}\)
\( = 2\sqrt{3} + \sqrt{3} - \sqrt{(\sqrt 3 -1)^2}\)
\( = 3\sqrt{3} - (\sqrt 3 -1) = 2\sqrt{3} + 1\)
2)
a)
Với \(x > 0; x ≠ 1\), ta có:
\(B = \left(\dfrac{1}{x-\sqrt x} + \dfrac{1}{\sqrt x -1} \right): \dfrac{\sqrt x+1}{(\sqrt x -1)^2}\)
\(=\dfrac{1+\sqrt x }{\sqrt x(\sqrt x -1)} . \dfrac{(\sqrt x -1)^2}{\sqrt x+1}\)
\(=\dfrac{\sqrt x -1 }{\sqrt x} \)
b)
Để \(B = \dfrac{1}3\)
\(\Leftrightarrow \dfrac{\sqrt x -1 }{\sqrt x} = \dfrac{1}3\)
\(\Leftrightarrow 3(\sqrt x-1)= \sqrt x\)
\(\Leftrightarrow \sqrt x = \dfrac{3}2\) \(\Leftrightarrow x = \dfrac{9}4\) (tm đkxđ)
KL.....
Câu 2.
a)
\(4x^4 + x^2 - 3 = 0\)
\(\Leftrightarrow (4x^2 -3)(x^2 +1) = 0\)
\(\Leftrightarrow x^2 = \dfrac{3}4\) (vì \(x^2+1 \geq 1 > 0 \) với mọi x)
\(\Leftrightarrow x = \dfrac{±\sqrt 3}2\).
b)
\(\left\{ \matrix{ \dfrac{3}2x - y = 1 \hfill \cr -5x + 4y = -3 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ x = 1 \hfill \cr y = \dfrac{1}2 \hfill \cr} \right.\)
Câu 3.
Trong mặt phẳng toạ độ Oxy cho (P): \(y = \dfrac{1}2 x^2\)
a)
Ta thấy:
\(-\dfrac{1}2 ≠ \dfrac{1}2 (-1)^2\)
Suy ra điểm \(H(-1;-\dfrac{1}2)\) không thuộc đồ thị hàm số (P).
b)
Với tung độ = 8, ta có:
\(8= \dfrac{1}2 x^2\)
\(\Leftrightarrow \left[ \matrix{ {x} = {4} \hfill \cr {x} = {-4} \hfill \cr} \right.\)
⇒ Các điểm thuộc đồ thị hàm số (P) có tung độ bằng 8 là (4;8) và (-4;8)
c)
Đường thẳng (d) đi qua M(0;2) có dạng: y - 2 = a(x - 0) ⇔ y = ax + 2.
Xét phương trình hoành độ giao điểm của (P) và (d), ta có:
\( \dfrac{1}2 x^2 = ax + 2 \Leftrightarrow x^2 - 2ax - 4 = 0\)
Ta thấy \(\Delta' = a^2 + 4 > 0\) với mọi a nên (d) luôn cắt (P) tại 2 điểm phân biệt.
Gọi 2 điểm đó lần lượt là \(A(x_1; \dfrac{1}2 x_1^2) \) và \(B(x_2;\dfrac{1}2 x_2^2) \), áp dụng hệ thức Vi-ét ta có:
\( \left\{ \matrix{ x_1+x_2 = 2a \hfill \cr x_1x_2 = -4 \hfill \cr} \right.\)
Ta có:
\({OA}^2 + {OB}^2 = x_1^2 + \dfrac{1}4x_1^4 + x_2^2 + \dfrac{1}4x_2^4 \)
\( = (x_1-x_2)^2 + 2x_1x_2 + \left(\dfrac{1}2x_1^2-\dfrac{1}2x_2^2 \right)^2 + 2.\dfrac{1}4x_1^2x_2^2\)
\( = (x_1-x_2)^2 + \left(\dfrac{1}2x_1^2-\dfrac{1}2x_2^2 \right)^2 -2.4+ \dfrac{1}2(-4)^2\)
\( = (x_1-x_2)^2 + \left(\dfrac{1}2x_1^2-\dfrac{1}2x_2^2 \right)^2 = {AB}^2\)
Hay \({OA}^2 + {OB}^2 = {AB}^2\), theo định lý Pytago thì △AOB luôn vuông tại O (đpcm).
Câu 4.
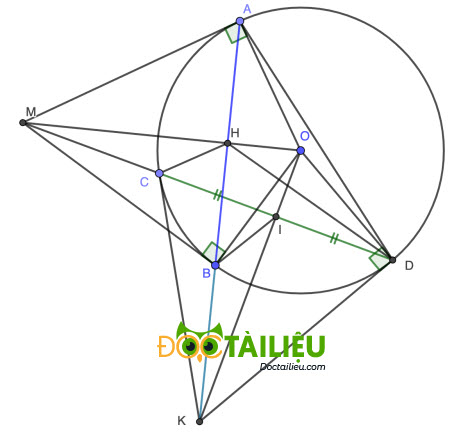
a)
Vì MB là tiếp tuyến tại B của (O) ⇒ ∠MBO = 90°.
Vì I là trung điểm CD, theo tính chất dây cung ta có OI ⊥ CD hay ∠MIO = 90° = ∠MBO ⇒ hai điểm B, I cùng thuộc đường tròn đường kính MO
Hay bốn điểm M, I, O, B cùng thuộc một đường tròn (đpcm).
b)
Ta có: ∠MAC = ∠ADC (tính chất góc tạo bởi tia tiếp tuyến và dây cung) hay ∠MAC = ∠MDA.
Xét △MAC và △MDA, ta có:
Góc AMD chung
∠MAC = ∠MDA (cmt)
Suy ra △MAC ∽ △MDA ⇒ \(\dfrac{MA}{MC} = \dfrac{MD}{MA}\) ⇒ MA² = MC.MD (đpcm).
c)
Xét △MAH và △MOA, ta có:
Góc AMO chung
∠MHA = ∠MAO (cùng = 90°)
Suy ra △MAH ∽ △MOA ⇒ \(\dfrac{MA}{MH} = \dfrac{MO}{MA}\) ⇒ MA² = MH.MO = MC.MD (cmt)
⇒ \(\dfrac{MC}{MH} = \dfrac{MO}{MD}\).
Xét △MHC và △MDO, ta có:
Góc OMD chung
\(\dfrac{MC}{MH} = \dfrac{MO}{MD}\) (cmt)
Suy ra △MHC ∽ △MDO ⇒ ∠MDO = ∠MHC = 180° - ∠CHO ⇒ ∠CHO + ∠CDO = 180°
⇒ Tứ giác CHOD nội tiếp (đpcm).
⇒ ∠OHD = ∠OCD (góc nội tiếp cùng chắn cung OD) = ∠CDO (△OCD cân tại O do OC = OD = R)
Vì △MHC ∽ △MDO ⇒ ∠MHC = ∠MDO = ∠CDO = ∠OHD (cmt)
⇔ 90° - ∠MHC = 90° - ∠OHD ⇔ ∠CHB = ∠BHD ⇒ HB là phân góc nhỏ CHD hay HA là phân giác góc lớn CHD (đpcm).
d)
Ta có: ∠ODK = ∠OCK = 90° (tính chất tiếp tuyến) ⇒ tứ giác OCKD nội tiếp, mà ta lại có tứ giác CHOD nội tiếp (cmt) ⇒ năm điểm K, C, H, O, D cùng thuộc một đường tròn.
⇒ ∠OHK = ∠OCK = 90° hay OH ⊥ HK (1)
Theo tính chất tiếp tuyến, ta lại có OH ⊥ AB, hay OH ⊥ HB (2)
Từ (1) và (2) ⇒ A, H, B, K thẳng hàng (đpcm).
Câu 5.
Áp dụng BĐT AM-GM ta có:
\(x^2 + y^2 \geq \dfrac{(x+y)^2}2\)
\(\Leftrightarrow 3x^2 + 3y^2 \geq \dfrac{3(x+y)^2}2\)
\(\Leftrightarrow 3x^2 + 3y^2 +(x+y)^2 \geq \dfrac{5(x+y)^2}2\)
\(\Leftrightarrow 4x^2 +2xy+ 4y^2 \geq \dfrac{5(x+y)^2}2\)
\(\Leftrightarrow \sqrt{2x^2 +xy+ 2y^2} \geq \sqrt{\dfrac{5(x+y)^2}4} = \dfrac{(x+y).\sqrt 5}2\)
Tương tự, ta chứng minh được:
\(\sqrt{2y^2 +yz+ 2z^2} \geq \dfrac{(y+z).\sqrt 5}2\)
\(\sqrt{2z^2 +zx+ 2x^2} \geq \dfrac{(z+x).\sqrt 5}2\)
Cộng vế theo vế 3 BĐT trên ta có:
\(\sqrt{2x^2 + xy + 2y^2}+ \sqrt{2y^2 + yz + 2z^2}+ \sqrt{2z^2 + zx + 2x^2} \geq \dfrac{\sqrt 5}2 (2x+2y+2z) = \sqrt 5\)
(ĐPCM)
Dấu bằng xảy ra \(\Leftrightarrow x=y=z= \dfrac{1}3\).
-/-
Đọc tài liệu vừa chia sẻ đến các em đề thi thử vào 10 môn Toán của phòng GD&ĐT huyện Lý Nhân năm 2020, còn rất nhiều bộ đề thi thử vào lớp 10 môn Toán của các trường khác trên cả nước đã được chúng tôi biên tập, thường xuyên truy cập vào trang để cập nhật nhé
