Cùng Đọc tài liệu thử sức với đề thi thử tuyển sinh vào lớp 10 môn toán năm 2020 lần thứ 2 tại Hà Tĩnh vừa diễn ra em nhé:
Đề thi thử
Bài 1. (2,0 điểm) Rút gọn các biểu thức sau:
a) \(A = \sqrt{12} + \sqrt{(2-\sqrt 3)^2}\)
b) \(B = \left( \dfrac{x-3\sqrt x}{x-9} + \dfrac{1}{\sqrt x+3} \right).\dfrac{1}{\sqrt x+1} \) (với \(x\geq 0; x ≠ 9\))
Bài 2. (2,0 điểm)
a) Cho hàm số bậc nhất: \(y = (1-\sqrt 2) x + m\) (1) (m là tham số)
- Hàm số (1) đồng biến hay nghịch biến? Vì sao?
- Tìm giá trị m để đồ thị hàm số (1) đi qua điểm \(A(-1;\sqrt2)\).
b) Trong mặt phẳng toạ độ Oxy, cho hai đường thẳng
(d): \(y = (n^2 + 2)x - n\)
(d'): \(y = 3x + 1\)
(n là tham số).
Tìm giá trị của n để hai đường thẳng (d) và (d') song song với nhau.
Bài 3. (2,0 điểm)
a) Tìm toạ độ giao điểm của đồ thị các hàm số: \(y = - x^2\) và \(y = 7x + 6\).
b) Cho phương trình bậc hai:
\(x^2 - 2x - m + 2 = 0\) (m là tham số)
Tìm giá trị của m để phương trình đã cho có hai nghiệm x1, x2 thoả mãn:
\(x_1-x_2 - 4 = 0\)
Bài 4. (3,0 điểm) Cho đường tròn (O) đường kính AB = 2R. Trên đường tròn (O) lấy điểm C bất kì (C không trùng với A, B). Tiếp tuyến của đường tròn tại A cắt tia BC tại D. Gọi H là hình chiếu của A trên đường thẳng DO. Tia AH cắt đường tròn (O) tại điểm E (E khác A).
a) Chứng minh tứ giác ADCH nội tiếp được đường tròn.
b) Chứng minh BC.BD = 4R².
c) Gọi F là trung điểm của BC. Chứng minh tam giác BOF đồng dạng với tam giác EHC.
Bài 5. (1,0 điểm) Cho ba số thực dương a, b, c thoả mãn:
(a + b)(b + c)(c + a) = 1.
Tìm giá trị nhỏ nhất của biểu thức:
\(F = \dfrac{1}{ab} + \dfrac{1}{bc} + \dfrac{1}{ca} \)
Hết
Trên đây là 5 câu hỏi trong đề thi thử tuyển sinh vào lớp 10 mới nhất lần thứ 2 với môn Toán ở Hà Tĩnh, cùng làm bài thi này trong 120 phút rồi đối chiếu với đáp án chi tiết dưới đây em nhé:
Giải chi tiết
Bài 1.
a) \(A = \sqrt{12} + \sqrt{(2-\sqrt 3)^2} =2 \sqrt{3} + 2 - \sqrt{3} = \sqrt{3} + 2\)
b)
Với \(x\geq 0; x ≠ 9\), ta có:
\(B = \left( \dfrac{x-3\sqrt x}{x-9} + \dfrac{1}{\sqrt x+3} \right).\dfrac{1}{\sqrt x+1} \)
\( = \left( \dfrac{\sqrt x(\sqrt x-3)}{(\sqrt x-3)(\sqrt x+3)} + \dfrac{1}{\sqrt x+3} \right).\dfrac{1}{\sqrt x+1} \)
\( = \dfrac{\sqrt x+1}{\sqrt x+3} .\dfrac{1}{\sqrt x+1} = \dfrac{1}{\sqrt x+3}\).
Bài 2.
a)
Vì \(1 - \sqrt 2 < 0\) ⇒ hàm số đã cho nghịch biến.
Để (1) đi qua điểm \(A(-1;\sqrt2)\), tức là toạ độ điểm A thoả mãn phương trình (1), hay:
\(\sqrt 2= -(1-\sqrt 2) + m\)
\(\Leftrightarrow m = 1\)
b)
Để hai đường thẳng (d) và (d') song song với nhau khi và chỉ khi:
\(\left\{ \matrix{ n^2 + 2 = 3 \hfill \cr -n ≠1 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ n = ±1 \hfill \cr -n ≠1 \hfill \cr} \right. \Rightarrow n = 1\).
KL....
Bài 3.
a)
Phương trình hoành độ giao điểm của đồ thị hai hàm số đã cho là:
\( - x^2 = 7x+6\)
\(\Leftrightarrow x^2 + 7x+6 =0\)
\(\Leftrightarrow \left[ \matrix{ {x} = -1 \Rightarrow y = -1 \hfill \cr {x} = -6 \Rightarrow y = -36 \hfill \cr} \right.\)
KL: giao điểm của 2 đồ thị đã cho là (-1;-1) và (-6;-36).
b)
Để phương trình đã cho có hai nghiệm khi:
\(\Delta' = 1 + m - 2 \geq 0 \Leftrightarrow m \geq 1\)
Áp dụng hệ thức Vi-ét cho phương trình đã cho ta có:
\(\left\{ \matrix{ x_1+x_2 = 2 \hfill \cr x_1x_2 = 2-m \hfill \cr} \right.\)
Ta có:
\(x_1-x_2 - 4 = 0 \Leftrightarrow x_1-x_2 = 4 \)
\( \Leftrightarrow (x_1-x_2)^2 = 16 \Leftrightarrow (x_1+x_2)^2 - 4x_1x_2 = 16\)
\( \Leftrightarrow 2^2 - 4(2-m) = 16 \Leftrightarrow m = 5\) (thoả mãn đk trên).
KL.....
Bài 4.
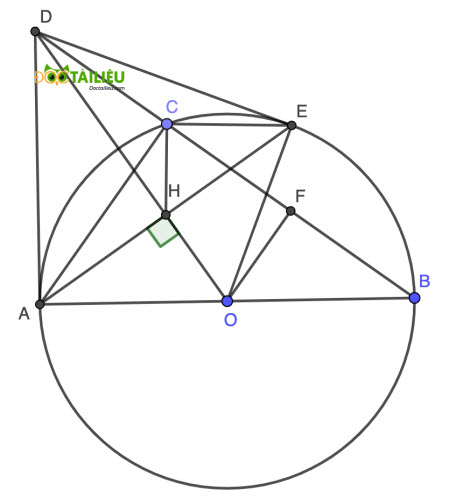
a)
Theo giả thiết có AH ⊥ DO ⇒ ∠AHD = 90°.
Vì C nội tiếp (O), đường kính AB ⇒ ∠ACB = 90°, hay ⇒ ∠ACD = ∠AHD = 90°
⇒ C và H cùng thuộc đường tròn đường kính AD, hay tứ giác ADCH nội tiếp (đpcm).
b)
Vì DA là tiếp tuyến tại A của (O) ⇒ ∠DAB = 90°.
Xét △BCA và △BAD ta có:
∠BCA = ∠DAB (= 90°)
Góc CBA chung
Suy ra △BCA ∽ △BAD ⇒ \(\dfrac{BC}{BA} = \dfrac{BA}{BD} \) ⇒ BC.BD = BA² = 4R² (đpcm).
c)
Vì tứ giác ADCH nội tiếp ⇒ ∠DAC = ∠DHC.
xét △BAC có O là trung điểm AB, F là trung điểm BC ⇒ OF // AC ⇒ ∠CAB = ∠FOB (góc đồng vị).
Ta có:
∠EHC = 90° - ∠DHC = 90° - ∠DAC = ∠CAB = ∠FOB.
Xét △BOF và △EHC ta có:
∠CEH = ∠FBO (góc nội tiếp (O) cùng chắn cung AC)
∠EHC = ∠FOB
Suy ra △BOF ∽ △EHC (đpcm).
Bài 5.
Áp dụng BĐT AM-GM ta có:
\((a+b)^2 \geq 4ab\)
\(\Leftrightarrow \dfrac{1}{ab} \geq \dfrac{4}{(a+b)^2}\)
Chứng minh tương tự, ta có:
\(F = \dfrac{1}{ab} + \dfrac{1}{bc} + \dfrac{1}{ca} \geq \dfrac{4}{(a+b)^2} + \dfrac{4}{(b+c)^2} + \dfrac{4}{(c+a)^2}\)
Áp dụng BĐT AM-GM ta có:
\( \dfrac{4}{(a+b)^2} + \dfrac{4}{(b+c)^2} + \dfrac{4}{(c+a)^2} \geq 3\sqrt[3]{\dfrac{4^3}{(a+b)^2(b+c)^2(c+a)^2}} = 12\)
Suy ra \(F \geq 12\).
Vậy \({Min}_F = 12 \Leftrightarrow a=b=c = \dfrac{1}2\).
-/-
Trên đây là hướng dẫn giải chi tiết đề thi thử vào 10 môn toán năm 2020 tại Hà Tĩnh, mong rằng đây sẽ là tài liệu hữu ích giúp các em ôn tập. Đừng quên còn rất nhiều tài liêu đề thi thử vào lớp 10 môn toán khác của các tỉnh thành trên cả nước nhé.
