Kỳ thi tuyển sinh vào lớp 10 chuyên Toán tại Hà Nội được diễn ra riêng biệt tại các trường THPT tuyển sinh riêng và sau kỳ thi tuyển sinh vào lớp 10 công lập, cùng Đọc tài liệu thử sức với một đề thi khá hay của trường THCS&THPT Lương Thế Vinh ra đề em nhé!
Dưới đây là đề thi thử vào lớp 10 môn Toán (chuyên) năm 2020 để các em thử sức:
Đề thi thử
Bài 1: (2 điểm)
1. Cho \(x = \dfrac{3}{\sqrt[3]4 - \sqrt[3]2 + 1}\); \(y = \dfrac{6}{4+\sqrt[3]4 + \sqrt[3]{16}}\).
Chứng minh rằng x + y là số tự nhiên.
2. Cho a, b, c là các số thực dương thoả mãn a + b + c = 5 và \(\sqrt a + \sqrt b + \sqrt c = 3\).
Chứng minh rằng:
\(\dfrac{\sqrt a}{a+2} + \dfrac{\sqrt b}{b+2} + \dfrac{\sqrt c}{c+2} = \dfrac{4}{\sqrt{(a+2)(b+2)(c+2)}} \)
Bài 2: (2,5 điểm)
1. Giải phương trình:
\(x^2 + 6x + 1 = (2x+1) \sqrt{x^2+2x+3}\)
2. Giải hệ phương trình:
\(\left\{ \matrix{ (x+y)^2 (8x^2 + 8y^2 + 4xy -13) + 5 = 0 \hfill \cr 2x +\dfrac{1}{x+y} = 1 \hfill \cr} \right.\)
Bài 3: (1 điểm)
Tìm các số nguyên x, y thoả mãn:
\(x^2y^2 - x^2 - 8y^2 =2xy\)
Bài 4: (1 điểm)
Cho đường tròn tâm O có hai đường kính AB và CD vuông góc với nhau. E là điểm tuỳ ý trên cung nhỏ BD (E khác B và D). AE cắt CD tại M, CE cắt AB tại N. Chứng minh:
\(\dfrac{MD}{MO} + \dfrac{NB}{NO} \geq 2\sqrt 2\)
Bài 5: (2,5 điểm)
Cho 3 đường tròn (O₁), (O₂), (O₃) có tâm lần lượt là O₁, O₂, O₃ đôi một tiếp xúc nhau, trong đó (O₁) chứa (O₂) và (O₃) (cho (O₂) nhỏ hơn (O₃)). Biết (O₁) tiếp xúc với (O₂) và (O₃) lần lượt tại A và B còn (O₂) tiếp xúc ngoài với (O3) tại I. Tiếp tuyến chung của (O₂) và (O₃) tại I cắt (O₁) tại E và F (cho EI > FI). Gọi D là trung điểm của EF, nối EA, EB cắt (O₂), (O₃) thứ tự tại M và N (M khác A, N khác B).
1. Chứng minh I là tâm đường tròn nội tiếp tam giác ABD.
2. Chứng minh MN là tiếp tuyến của (O₃).
Bài 6: (1 điểm)
Cho các số a,b,c thoả mãn:
\(|a| + |b|+|c| > 17\)
Chứng minh rằng luôn tìm được số x₀ thoả mãn \(0 \leq x_0 \leq 1\) để:
\(|ax_0^2 + bx_0 + c| > 1\)
---Hết---
Xem thêm các tài liệu đề thi thử toán vào lớp 10 tại Hà Nội năm 2020 nữa em nhé!
Đáp án
Bài 1:
1.
Ta có:
\(x = \dfrac{3}{\sqrt[3]4 - \sqrt[3]2 + 1} = \dfrac{3(\sqrt[3]2+1)}{(\sqrt[3]2+1)(\sqrt[3]4 - \sqrt[3]2 + 1)} = \dfrac{3(\sqrt[3]2+1)}{3} = \sqrt[3]2+1\)
\(y = \dfrac{6}{4+\sqrt[3]4 + \sqrt[3]{16}}= \dfrac{6(\sqrt[3]4-1)}{(\sqrt[3]4-1)\sqrt[3]4(\sqrt[3]{4^2}+1 + \sqrt[3]{4})} = \dfrac{6(\sqrt[3]4-1)}{3\sqrt[3]4} = \sqrt[3]2(\sqrt[3]4-1)\)
Suy ra:
\(x + y = \sqrt[3]2+1 + \sqrt[3]2(\sqrt[3]4-1) = \sqrt[3]2+1 + 2 - \sqrt[3]2 = 3\).
Vì 3 là số tự nhiên ⇒ x + y là số tự nhiên (đpcm).
2.
Ta có:
\(a + b + c = 5 \Rightarrow b+c = 5-a\)
Và:
\(\sqrt a + \sqrt b + \sqrt c = 3 \Rightarrow \sqrt b + \sqrt c = 3 - \sqrt a \)
\(\Rightarrow (\sqrt b + \sqrt c)^2 = (3 - \sqrt a)^2 \Rightarrow b+c+ 2\sqrt {bc} = (3 - \sqrt a)^2\)
\( \Rightarrow \sqrt {bc} = \dfrac{(3 - \sqrt a)^2}2 + \dfrac{a - 5}2\) \( \Rightarrow \sqrt {bc} = a - 3\sqrt a+2\)
\( \Rightarrow bc = (a - 3\sqrt a+2)^2\)
Ta có:
\(\sqrt{\dfrac{ a(b+2)(c+2)}{a+2}} = \sqrt{\dfrac{ a(bc + 2b + 2c + 4)}{a+2}}\)
\( = \sqrt{\dfrac{ a[(a - 3\sqrt a+2)^2 + 2(5-a) + 4]}{a+2}}\)
\( = \sqrt{\dfrac{ a(a^2 - 6a\sqrt a + 11a -12 \sqrt a + 18)}{a+2}}\)
\( = \sqrt{\dfrac{ a(a+2)(a-6\sqrt a+9)}{a+2}}\)
\( = \sqrt{a(3-\sqrt a)^2} = \sqrt{a(\sqrt b + \sqrt c)^2} = \sqrt{a}(\sqrt b + \sqrt c) \)
Tương tự, ta có:
\(\sqrt{\dfrac{ a(b+2)(c+2)}{a+2}} + \sqrt{\dfrac{ b(c+2)(a+2)}{b+2}} + \sqrt{\dfrac{ c(a+2)(b+2)}{c+2}} = \sqrt{a}(\sqrt b + \sqrt c) + \sqrt{b}(\sqrt c + \sqrt a) + \sqrt{c}(\sqrt a + \sqrt b) \)
\( = 2 (\sqrt{ab} + \sqrt{bc} + \sqrt {ca}) = (\sqrt a + \sqrt b + \sqrt c)^2 - (a+b+c) = 3^2 - 5 = 4\)
\(\Leftrightarrow \sqrt{\dfrac{ a(b+2)(c+2)}{a+2}} + \sqrt{\dfrac{ b(c+2)(a+2)}{b+2}} + \sqrt{\dfrac{ c(a+2)(b+2)}{c+2}} = 4\)
\(\Leftrightarrow \dfrac{\sqrt a}{a+2} + \dfrac{\sqrt b}{b+2} + \dfrac{\sqrt c}{c+2} = \dfrac{4}{\sqrt{(a+2)(b+2)(c+2)}} \) (đpcm).
Bài 2:
1.
Cách 1:
Đặt \(a = \sqrt{x^2+2x+3}\) (\(a\geq 0\))
\(b = 2x+ 1\)
Phương trình đã cho tương đương với:
\(a^2 + 2b - 4 = ab \)
\(\Leftrightarrow a^2 - 4 + 2b - ab = 0\)
\(\Leftrightarrow (a-2)(a+2-b) = 0\)
\(\Leftrightarrow \left[ \matrix{ a= 2 \hfill \cr a = b- 2\hfill \cr} \right.\)
\(\Leftrightarrow \left[ \matrix{ \sqrt{x^2+2x+3}= 2 \hfill \cr \sqrt{x^2+2x+3}= 2x - 1\hfill \cr} \right.\)
\(\Leftrightarrow \left[ \matrix{ {x^2+2x+3}= 4 \hfill \cr {x^2+2x+3}= (2x - 1)^2 \space (2x-1 \geq0 \Leftrightarrow x \geq \dfrac{1}2)\hfill \cr} \right.\)
\(\Leftrightarrow \left[ \matrix{ {x^2+2x-1}=0 \hfill \cr 3x^2 - 6x - 2 = 0\hfill \cr} \right.\)
\(\Leftrightarrow \left[ \matrix{ x = -1 + \sqrt 2 \hfill \cr x = -1 - \sqrt 2 \hfill \cr x = \dfrac{3+\sqrt {15}}3 \hfill \cr x = \dfrac{3-\sqrt {15}}3 \space (loại \space vì \space x\geq \dfrac{1}2) \hfill \cr} \right. \)
KL......
Cách 2:
\(x^2 + 6x + 1 = (2x+1) \sqrt{x^2+2x+3}\)
\(\Rightarrow (x^2 + 6x + 1)^2 = (2x+1)^2(x^2+2x+3)\)
\(\Leftrightarrow x^4 + 12x^3 + 38x^2 + 12x + 1 = (4x^2+4x+1)(x^2+2x+3)\)
\(\Leftrightarrow x^4 + 12x^3 + 38x^2 + 12x + 1 = 4x^4 + 12 x^3 + +21x^2 + 14x + 3\)
\(\Leftrightarrow 3x^4 -17x^2 + 2x + 2 = 0\)
\(\Leftrightarrow (x^2 + 2x - 1)(3x^2 - 6x -2) = 0\)
\(\Leftrightarrow \left[ \matrix{ x^2 + 2x - 1 = 0 \hfill \cr 3x^2 - 6x -2 = 0 \hfill \cr} \right. \)
\(\Leftrightarrow \left[ \matrix{ x = -1 + \sqrt 2 \hfill \cr x = -1 - \sqrt 2 \hfill \cr x = \dfrac{3+\sqrt {15}}3 \hfill \cr x = \dfrac{3-\sqrt {15}}3 \space (loại) \hfill \cr} \right. \)
KL......
2. Giải hệ phương trình:
\(\left\{ \matrix{ (x+y)^2 (8x^2 + 8y^2 + 4xy -13) + 5 = 0 \hfill \cr 2x +\dfrac{1}{x+y} = 1 \hfill \cr} \right.\)
(ĐKXĐ x + y ≠ 0)
\( pt(1) \Leftrightarrow [8(x + y)^2 - 12xy -13]+ \dfrac{5}{(x+y)^2} = 0 \)
\(\Leftrightarrow 5(x + y)^2 + \dfrac{5}{(x+y)^2} =12xy+ 13 - 3(x+y)^2 \)
\(\Leftrightarrow 13 - 3(x-y)^2 = 5(x + y)^2 + \dfrac{5}{(x+y)^2} \geq 2\sqrt{5(x + y)^2 . \dfrac{5}{(x+y)^2}} = 10\)
\(\Leftrightarrow 3 \geq 3(x-y)^2 \Leftrightarrow (x-y)^2 \leq 1\) (*)
Ta có:
\(pt(2) \Leftrightarrow \dfrac{1}{x+y} = 1 -2x\)
\(\Leftrightarrow x+ y = \dfrac{1}{1 -2x}\)
\(\Leftrightarrow y -x = \dfrac{1}{1 -2x} - 2x = \dfrac{1-2x+4x^2}{1 -2x} \)
\(\Leftrightarrow (y -x)^2 = \dfrac{(1-2x+4x^2)^2}{(1 -2x)^2} \)
Từ (*) \(\Rightarrow (y -x)^2 = \dfrac{(1-2x+4x^2)^2}{(1 -2x)^2} \leq 1\)
\(\Leftrightarrow (1-2x+4x^2)^2 \leq (1 -2x)^2\)
\(\Leftrightarrow (1-2x+4x^2)^2 - (1 -2x)^2 \leq 0\)
\(\Leftrightarrow (1-2x+4x^2-1 + 2x)(1-2x+4x^2+1 - 2x) \leq 0\)
\(\Leftrightarrow 4x^2(4x^2-4x + 2) \leq 0\)
\(\Leftrightarrow 4x^2[(2x-1)^2 + 1] \leq 0\)
Mà \((2x-1)^2 + 1 \geq 1 > 0 \Rightarrow 4x^2 \leq 0 \Rightarrow x = 0\).
Thay x = 0 vào hệ đầu ta tìm được y = 1.
KL....
Bài 3:
Dễ thấy nếu x = 0 thì y = 0 và ngược lại.
Với x,y ≠ 0 ta có:
\(x^2y^2 - x^2 - 8y^2 =2xy\)
\(\Leftrightarrow x^2y^2 -7y^2 = x^2 + 2xy + y^2\)
\(\Leftrightarrow y^2(x^2 -7) = (x+y)^2\)
\(\Leftrightarrow y^2(x^2 -7) = (x+y)^2\) (1)
\(\Rightarrow (x+y)^2⋮ y^2\)
\(\Leftrightarrow (x+y)⋮ y \Leftrightarrow x⋮ y \)
Đặt: \(x = ky \) (k ∈ ℤ), ta có:
(1) \(\Leftrightarrow y^2(k^2y^2 - 7) = (ky + y)^2\)
\(\Leftrightarrow k^2y^2 - 7 = (k + 1)^2\)
\(\Leftrightarrow k^2y^2 - (k + 1)^2 = 7\)
\(\Leftrightarrow (ky - k - 1)(ky+k+1) = 7\)
\(\Leftrightarrow \left[ \matrix{ \left\{ \matrix{ ky - k - 1 = 1 \hfill \cr ky+k+1 = 7 \hfill \cr} \right.\hfill \cr \left\{ \matrix{ ky - k - 1 = 7 \hfill \cr ky+k+1 = 1 \hfill \cr} \right.\hfill \cr \left\{ \matrix{ ky - k - 1 = -1 \hfill \cr ky+k+1 = -7 \hfill \cr} \right.\hfill \cr \left\{ \matrix{ ky - k - 1 = -7 \hfill \cr ky+k+1 = -1 \hfill \cr} \right. \hfill \cr} \right. \)
\(\Leftrightarrow \left[ \matrix{ \left\{ \matrix{ ky =4 \hfill \cr k = 2 \hfill \cr} \right.\hfill \cr \left\{ \matrix{ ky = 4\hfill \cr k =-4 \hfill \cr} \right.\hfill \cr \left\{ \matrix{ ky =-4 \hfill \cr k = -4 \hfill \cr} \right.\hfill \cr \left\{ \matrix{ ky = -4 \hfill \cr k= 2 \hfill \cr} \right. \hfill \cr} \right. \)
\(\Leftrightarrow \left[ \matrix{ (x;y) = (4;2) \hfill \cr (x;y) = (4;-1) \hfill \cr (x;y) = (-4;1) \hfill \cr (x;y) = (-4;-2)\hfill \cr} \right.\)
KL phương trình đã cho có 5 nghiệm nguyên .....
Bài 4:
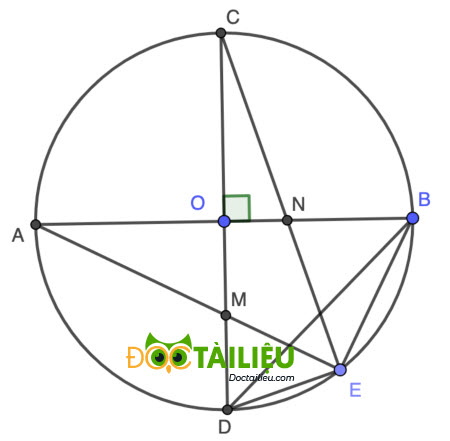
Gọi bán kinh của (O) là r. Ta có:
\(AB = CD = 2r\)
\(AC = \sqrt{{AO}^2+{OC}^2} = r\sqrt 2\)
Xét △MDE và △MAC có:
∠DME = ∠AMC (đối đỉnh)
∠MAC = ∠MDE (góc nội tiếp cùng chắn cung CE)
Suy ra △MDE ∽ △MAC ⇒ \(\dfrac{MD}{DE} = \dfrac{MA}{AC} \) ⇒ \(MD = \dfrac{MA.DE}{AC} \) (1)
Xét △AOM và △AEB có:
Góc MAO chung
∠AOM = ∠AEB (= 90°)
Suy ra △AOM ∽ △AEB ⇒ \(\dfrac{OM}{AM} = \dfrac{EB}{AB} \) ⇒ \(OM = \dfrac{AM.EB}{AB} \) (2)
Chia vế theo vế (1) với (2) ta có:
\(\dfrac{MD}{MO} = \dfrac{MA.DE}{AC} : \dfrac{AM.EB}{AB} = \dfrac{AB.DE}{AC.EB} = \dfrac{2r.DE}{r\sqrt2.EB} = \dfrac{DE\sqrt2}{EB} \)
Tương tự, ta có:
\(\dfrac{NB}{NO} = \dfrac{BE\sqrt2}{ED} \)
Cộng vế theo vế 2 đẳng thức trên, ta có:
\(\dfrac{MD}{MO} + \dfrac{NB}{NO} =\dfrac{DE\sqrt2}{EB} +\dfrac{BE\sqrt2}{ED} \geq 2\sqrt {\dfrac{DE\sqrt2}{EB} .\dfrac{BE\sqrt2}{ED}} = 2\sqrt 2\) (đpcm).
Dấu bằng xảy ra ⇔ E là điểm chính giữa cung BD.
Bài 5:
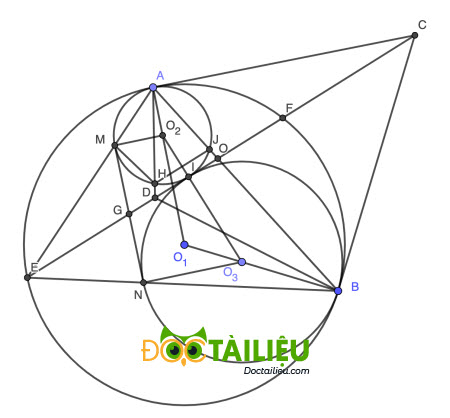
1.
Kẻ tiếp tuyến tại A và B của (O₁) cắt nhau tại C.
Dễ thấy AC là trục đẳng phương của (O₁) và (O₂); BC là trục đẳng phương của (O₁) và (O₃); EF là trục đẳng phương của (O₂) và (O₃) ⇒ AC, BC, EF đồng quy hay E,F,C thẳng hàng.
Vì A, B là các tiếp điểm nên O₁, O₂, A thẳng hàng và O₁, O₃, B thẳng hàng.
Vì D là trung điểm EF ⇒ O₁D ⊥ EF ⇒ ∠O₁AC = ∠O₁DC = ∠O₁BC = 90° ⇒ 5 điểm O₁, D, A, C, B cùng thuộc đường tròn đường kính O₁C.
Suy ra ∠BDC = ∠BAC = ∠CBA = ∠CDA ⇒ DI là phân giác của ∠ADB (1).
Gọi AD, AO cắt (O₂) lần lượt tại H và J. Ta có:
\(∠AHJ = \dfrac{1}2 ∠AO_2J = 90° - ∠O_2AJ = ∠BAC = ∠CDA\)
⇒ HJ // DI, mà lại có DI ⊥ O₂I ⇒ HJ ⊥ O₂I hay I là điểm chính giữa cung DJ.
Suy ra AI là phân giác của ∠HAJ hay AI là phân giác của ∠DAB (2).
Từ (1) và (2) suy ra I là tâm đường tròn nội tiếp tam giác ABD (đpcm).
2.
Vì E thuộc trục đẳng phương của (O₂), (O₃) ⇒ EM.EA = EI² = EN.EB ⇒ AMNB là tứ giác nội tiếp
⇒ \(∠MNE = ∠MAJ = ∠EAB = \dfrac{1}2 ∠EO_1B = 90° - ∠O_1BN = 90° - ∠O_3NB\)
⇒ ∠MNE + ∠O₃NB = 90° = 180°- ∠MNO₃ ⇒ ∠MNO₃ = 90°
Suy ra MN là tiếp tuyến tại N của (O₃) (đpcm).
Bài 6:
Ta đi chứng minh bằng phản chứng.
Giả sử với mọi số x₀ thoả mãn \(0 \leq x_0 \leq 1\) thì:
\(|ax_0^2 + bx_0 + c| \leq 1\) (*)
Thay x₀ = 0 vào (*) ta có:
\(| c| \leq 1\)
\(\Leftrightarrow 17 < |a| + |b| + |c| \leq |a| + |b| + 1 \Rightarrow 16 < |a| + |b| \)
Áp dụng BĐT trị tuyệt đối: \(|x| - |y| \leq |x+y| \), ta có:
(*) \(\Leftrightarrow |ax_0^2 + bx_0| -| c| \leq |ax_0^2 + bx_0 + c| \leq 1\)
\(\Rightarrow |ax_0^2 + bx_0| \leq 1 + |c| \leq 2\) (**)
Với ab > 0, ta có: \(\left\{ \matrix{ |ab| = ab \hfill \cr |a+b| = |a|+|b| \hfill \cr} \right.\)
Thay x₀ = 1 vào (**) ta có:
\( |a| + |b| = |a + b| \leq 2\)
Lại có
\(16 < |a| + |b| = |a+b| \leq 2 \Rightarrow 16 < 2\) (vô lý)
Suy ra 0 > ab, tức là: \(|ab| = -ab\)
Thay \(x_0 = \dfrac{1}2\) vào (**) ta có:
\( \left|\dfrac{a}4 + \dfrac{b}2 \right| \leq 2\)
\(\Leftrightarrow \left|2a + 4b \right| \leq 16 < |a| + |b|\)
\(\Rightarrow (2a + 4b )^2 < (|a| + |b|)^2\)
\(\Leftrightarrow 4a^2 + 16ab + 16b^2 < a^2 + b^2 + 2|ab| \)
\(\Leftrightarrow 3a^2 + 18ab+ 15b^2 < 0\)
\(\Leftrightarrow 3a^2 - 18|ab|+ 15b^2 < 0\)
\(\Leftrightarrow 3(|a|-|b|)(|a|-5|b|) < 0\)
\(\Leftrightarrow |b| <|a| <5|b|\) (1)
Thay \(x_0 = \dfrac{1}4\) vào (**) ta có:
\( \left|\dfrac{a}{16} + \dfrac{b}4 \right| \leq 2 \Leftrightarrow \left|\dfrac{a}{2} + 2b \right| \leq 16 < |a|+|b|\)
\(\Rightarrow \left(\dfrac{a}{2} + 2b \right)^2 < (|a| + |b|)^2\)
\(\Leftrightarrow \dfrac{a^2}{4} + 4b^2 + 2ab < a^2 + b^2 + 2|ab| = a^2 + b^2 -2ab\)
\(\Leftrightarrow \dfrac{-3a^2}{4} + 3b^2 + 4ab < 0\)
\(\Leftrightarrow -3a^2 + 12b^2- 16|ab| < 0\)
\(\Leftrightarrow 3(-|a|+\dfrac{2}3|b|)(|a|-6|b|) < 0\)
\(\Leftrightarrow (|a|-\dfrac{2}3|b|)(|a|-6|b|) > 0\)
\(\Leftrightarrow \left[ \matrix{ |a| > 6|b| \hfill \cr |a| < \dfrac{2}3|b| \hfill \cr} \right.\)
Cả hai trường hợp trên đều mâu thuẫn với (1): \(|b| <|a| <5|b|\) nên vô lý.
Hay điều giả sử là sai, tức là ta có đpcm.
-/-
Đọc tài liệu vừa chia sẻ đến các em đề thi thử vào 10 môn Toán chuyên của THCS&THPT Lương Thế Vinh, còn rất nhiều bộ đề thi thử vào lớp 10 môn Toán của các trường khác trên cả nước đã được chúng tôi biên tập, thường xuyên truy cập vào trang để cập nhật nhé
