Cùng Đọc tài liệu thử sức với đề thi thử vào lớp 10 môn toán năm 2020 trường Lương Thế Vinh lần thứ hai em nhé:
Đề thi thử
|
TRƯỜNG THCS & THPT LƯƠNG THẾ VINH Lần thứ hai |
ĐỀ THI THỬ VÀO LỚP 10 Năm học: 2020 – 2021 MÔN: TOÁN Thời gian làm bài: 120 phút |
Bài 1. (2,0 điểm)
Cho các biểu thức
\(A=\dfrac{\sqrt{x}+15}{x-9}-\dfrac{x}{x-3\sqrt{x}}+ \dfrac{2\sqrt{x}+5}{\sqrt{x}+3}\)
và \(B=\dfrac{8\sqrt{x}-3}{14}\) với \(x\geq 0; x≠9\)
a, Rút gọn biểu thức A
b, Tìm x sao cho A = 2B
c, Chứng minh rằng không tồn tại giá trị của x để A nhận giá trị là số nguyên.
Bài 2. (2,0 điểm)
Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Một đội xe theo kế hoạch chở hết 200 tấn hàng trong một số ngày quy định. Do mỗi ngày đội đó chở vượt mức 5 tấn nên đội đã hoàn thành kế hoạch sớm hơn thời gian quy định 1 ngày và chở thêm được 25 tấn. Tính thời gian đội chở hết hàng theo kế hoạch.
Bài 3. (2,5 điểm)
1) Giải hệ phương trình:
\(\left\{ \matrix{ 2|x-y|+\dfrac{5}{y+5} = \dfrac{21}{2} \hfill \cr |x-y|-\dfrac{15}{2y+10} = \dfrac{17}{4} \hfill \cr} \right.\)
2) Cho parabol \((P): \space y=x^2\)
và \((d): \space y = 2(m-3)x+2m-5\)
a, Khi m = 4, hãy tìm tọa độ giao điểm của (P) và (d).
b, Tìm m để đường thẳng (d) cắt (P) tại hai điểm phân biệt A, B nằm khác phía của trục Oy sao cho tam giác OAB vuông tại O.
3) Tìm m để phương trình sau có bốn nghiệm phân biệt
\(x^4-(3m-2)x^2+3m-2=0\)
Bài 4. (3,0 điểm)
Cho đường tròn (O,R) và dây cung \(BC=R\sqrt{3}\) cố định. Một điểm A chuyển động trên cung lớn BC sao cho tam giác ABC có ba góc nhọn, AM là đường kính của (O). Kẻ các đường cao AD, BE, CF cắt nhau tại H.
a, Chứng minh các tứ giác BCEF, AEHF nội tiếp.
b, Chứng minh tứ giác BHCM là hình bình hành và tính độ dài của đoạn AH.
c, Kẻ DP vuông góc với BE tại P, đường thẳng qua P và vuông góc với đường kính AM cắt CF tại Q. Chứng minh rằng PQ ≤ HD
Bài 5. (0,5 điểm)
Cho a, b là các số thực dương làm cho phương trình sau có nghiệm:
\(x^2-2(a-2b)x+a^2+b^2=0\)
Tìm giá trị lớn nhất của biểu thức
\(P = \dfrac{ab}{a^2-2ab+3b^2}\)
Hết
Trên đây là 5 câu hỏi trong đề thi thử lớp 10 lần thứ 2 của trường Lương Thế Vinh với môn Toán, cùng làm bài thi trong 120 phút rồi đối chiếu với đáp án chi tiết dưới đây em nhé:
Đáp án đề thi thử vào lớp 10 môn Toán 2020 trường Lương Thế Vinh (lần 2)
Bài 1. (2,0 điểm)
a, Ta có:
\(A=\dfrac{\sqrt{x}+15}{x-9}-\dfrac{x}{x-3\sqrt{x}}+ \dfrac{2\sqrt{x}+5}{\sqrt{x}+3}\)
(ĐKXĐ \(x>0; x≠9\))
\(A=\dfrac{\sqrt{x}+15}{(\sqrt{x}+3)(\sqrt{x}-3)}-\dfrac{x}{\sqrt{x}(\sqrt{x}-3)}+ \dfrac{2\sqrt{x}+5}{\sqrt{x}+3}\)
\(=\dfrac{\sqrt{x}+15}{(\sqrt{x}+3)(\sqrt{x}-3)}-\dfrac{\sqrt{x}(\sqrt{x}+3)}{(\sqrt{x}+3)(\sqrt{x}-3)}+ \dfrac{(2\sqrt{x}+5)(\sqrt{x}-3)}{(\sqrt{x}+3)(\sqrt{x}-3)}\)
\(=\dfrac{(\sqrt{x}+15)-\sqrt{x}(\sqrt{x}+3)+(2\sqrt{x}+5)(\sqrt{x}-3)}{(\sqrt{x}+3)(\sqrt{x}-3)}\)
\(=\dfrac{\sqrt{x}+15-x-3\sqrt{x}+2x+5\sqrt{x}-6\sqrt{x}-15}{(\sqrt{x}+3)(\sqrt{x}-3)}\)
\(=\dfrac{x-3\sqrt{x}}{(\sqrt{x}+3)(\sqrt{x}-3)}\)
\(=\dfrac{\sqrt{x}(\sqrt{x}-3)}{(\sqrt{x}+3)(\sqrt{x}-3)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
Vậy \(A=\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
b, Để A = 2B, ta có:
\(A=2B\) \(\Leftrightarrow \dfrac{\sqrt{x}}{\sqrt{x}+3} = 2.\dfrac{8\sqrt{x}-3}{14}\)
\(\Leftrightarrow \dfrac{\sqrt{x}}{\sqrt{x}+3} = \dfrac{8\sqrt{x}-3}{7}\)
\(\Leftrightarrow 7\sqrt{x} = (8\sqrt{x}-3)(\sqrt{x}+3)\)
\(\Leftrightarrow 7\sqrt{x} =8x+21\sqrt{x}-9\)
\(\Leftrightarrow 8x+14\sqrt{x}-9=0\)
\(\Leftrightarrow (2\sqrt{x}-1)(4\sqrt{x}+9)=0\)
\(\Leftrightarrow 2\sqrt{x}-1=0\)
(vì \(4\sqrt{x}+9>0\) với \(x> 0; x≠9\))
\(\Leftrightarrow \sqrt{x} =\dfrac{1}{2}\)
\(\Leftrightarrow x=\dfrac{1}{4}\).
Vậy để \(A=2B\) \(\Leftrightarrow x=\dfrac{1}{4}\).
c, Chứng minh rằng không tồn tại giá trị của x để A nhận giá trị là số nguyên.
Ta có:
\(A=\dfrac{\sqrt{x}}{\sqrt{x}+3}\) \(=\dfrac{\sqrt{x}+3-3}{\sqrt{x}+3}\)
\(=1-\dfrac{3}{\sqrt{x}+3}\)
Để A là số nguyên \(\Leftrightarrow\) \( \dfrac{3}{\sqrt{x}+3}\) là số nguyên
\(\Leftrightarrow 3 ⋮ \sqrt{x}+3\)
\(\Leftrightarrow( \sqrt{x}+3) ∈ \{-3;-1;1;3\}\) (1)
Mà theo điều kiện xác định, ta có \(x> 0; x≠9\)
\(\Leftrightarrow \sqrt{x}+3 >3\) (2)
Từ (1) với (2) suy ra vô nghiệm, hay không tồn tại giá trị nào của x để A là số nguyên (đpcm).
Bài 2. (2,0 điểm)
Gọi số tấn hàng theo kế hoạch đội xe đó định chở ban đầu là x (tấn) (x > 0)
Khi đó số ngày quy định là:
\(\dfrac{200}{x}\) (ngày)
Do mỗi ngày chở vượt mức 5 tấn, đội đã hoàn thành kế hoạch sớm hơn thời gian quy định 1 ngày và chở thêm được 25 tấn, tức là:
\((x+5) \big(\dfrac{200}{x}-1\big) = 200+25\)
\(\Leftrightarrow (x+5) (200-x) = 225x\)
\(\Leftrightarrow -x^2+195x+1000 = 225x\)
\(\Leftrightarrow -x^2-30x+1000 = 0\)
\(\Leftrightarrow (20-x)(50+x) = 0\)
\(\Leftrightarrow x=20\) (vì x > 0)
Suy ra thời gian đội chở hết hàng theo kế hoạch là:
\(\dfrac{200}{x} = \dfrac{200}{20} =10\) (ngày)
Bài 3. (2,5 điểm)
1) Ta có:
\(\left\{ \matrix{ 2|x-y|+\dfrac{5}{y+5} = \dfrac{21}{2} \hfill \cr |x-y|-\dfrac{15}{2y+10} = \dfrac{17}{4} \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ 2|x-y|+5.\dfrac{1}{y+5} = \dfrac{21}{2} \hfill \cr |x-y|-\dfrac{15}{2}.\dfrac{1}{y+5} = \dfrac{17}{4} \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ 2|x-y|+5.\dfrac{1}{y+5} = \dfrac{21}{2} \hfill \cr 2|x-y|-15.\dfrac{1}{y+5} = \dfrac{17}{2} \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ 2|x-y|+5.\dfrac{1}{y+5} = \dfrac{21}{2} \hfill \cr 20.\dfrac{1}{y+5} = 2 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ |x-y| = \dfrac{21}{4}-\dfrac{5}{2}.\dfrac{1}{y+5} \hfill \cr \dfrac{1}{y+5} = \dfrac{1}{10} \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ |x-y| = \dfrac{21}{4}-\dfrac{5}{2}.\dfrac{1}{10}=5 \hfill \cr y+5= 10 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ |x-y| = 5 \hfill \cr y=5 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ \left[ \matrix{ {x} = {0} \hfill \cr {x} = 10 \hfill \cr} \right. \hfill \cr y=5 \hfill \cr} \right.\)
Vậy hệ đã cho có 2 bộ nghiệm là
\((x;y) = (0;5)\) hoặc \((x;y) = (10;5)\)
2) Cho parabol \((P): \space y=x^2\)
và \((d): \space y = 2(m-3)x+2m-5\)
a, Với m = 4, ta có:
\((d): \space y = 2(4-3)x+2.4-5\)
\(\Leftrightarrow (d): \space y = 2x+3\)
Ta thấy hoành độ giao điểm của (P) và (d) là nghiệm của phương trình:
\(x^2 = 2x+3\)
\(\Leftrightarrow x^2 -2x-3=0\)
\(\Leftrightarrow (x-3)(x+1)=0\)
\(\Leftrightarrow \left[ \matrix{ {x} = {3} \Rightarrow y = 9 \hfill \cr {x} = {-1} \Rightarrow y = 1 \hfill \cr} \right.\)
Vậy giao điểm của (P) và (d) là 2 điểm có tọa độ lần lượt là (3;9) và (-1;1)
b,
Ta thấy hoành độ giao điểm của (P) và (d) là nghiệm của phương trình:
\(x^2 = 2(m-3)x+2m-5\)
\(\Leftrightarrow x^2 - 2(m-3)x-2m+5=0\) (1)
Ta có:
\(\Delta' = (m-3)^2 +2m - 5\)
\( = m^2 -6m + 9 +2m - 5\)
\( = m^2 -4m + 4 \)
\( = (m-2)^2\) \(\geq 0\) với mọi m.
Để (d) cắt (P) tại 2 điểm phân biệt thì \(\Delta ' > 0\) hay \(m≠2\).
Ta có 2 nghiệm của phương trình (1) là:
\(x = m-3 ±\sqrt{\Delta'} = m-3 ± (m-2)\)
\(\Leftrightarrow \left[ \matrix{ {x} = 2m - 5 \Rightarrow y = (2m - 5)^2 \hfill \cr {x} = {-1} \Rightarrow y = 1\hfill \cr} \right.\)
Không mất tính tổng quát, ta gọi
\(A(-1;1)\) và \(B\big(2m-5;(2m-5)^2\big)\)
Để 2 điểm A B nằm khác phía của trục Oy thì:
\(x_A .x_B < 0\)
\(\Leftrightarrow -1.(2m-5) < 0\) \(\Leftrightarrow m > \frac{5}{2}\)Để tam giác OAB vuông tại O, theo Pythagores ta có:
\(AB^2 = OA^2 + OB^2\)
\(\Leftrightarrow (2m-5+1)^2 + [(2m-5)^2-1]^2 = 1+ 1 + (2m-5)^2 + [(2m-5)^2]^2\)
\(\Leftrightarrow (2m-5+1)^2 - (2m-5)^2 = 2+ [(2m-5)^2]^2- [(2m-5)^2-1]^2 \)
\(\Leftrightarrow 2(2m-5) + 1 = 2 + 2(2m-5)^2-1\)
\(\Leftrightarrow 2(2m-5) = 2(2m-5)^2\)
\(\Leftrightarrow 2(2m-5)(2m-5-1) = 0\)
\(\Leftrightarrow (2m-5)(2m-6) = 0\)
Vì \(\Leftrightarrow m > \frac{5}{2}\) (theo điều kiện để A B nằm khác phía của trục Oy), ta có:
\(m = 3\) (thỏa mãn)
Vậy \(m = 3\).
3)
\(x^4-(3m-2)x^2+3m-2=0\) (*)
Để (*) có 4 nghiệm phân biệt tức là phương trình:
\(x^2-(3m-2)x+3m-2=0\)
phải có 2 nghiệm phân biệt cùng dương, tức là:
\(\left\{ \matrix{ \Delta >0 \hfill \cr x_1+x_2 > 0 \hfill \cr x_1.x_2 > 0 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ (3m-2)(3m-6)>0 \hfill \cr 3m-2 > 0 \hfill \cr } \right.\)
\(\Leftrightarrow m>2\).
Vậy \( m>2\) thì phương trình (*) đã cho có 4 nghiệm phân biệt.
Bài 4. (3,0 điểm)
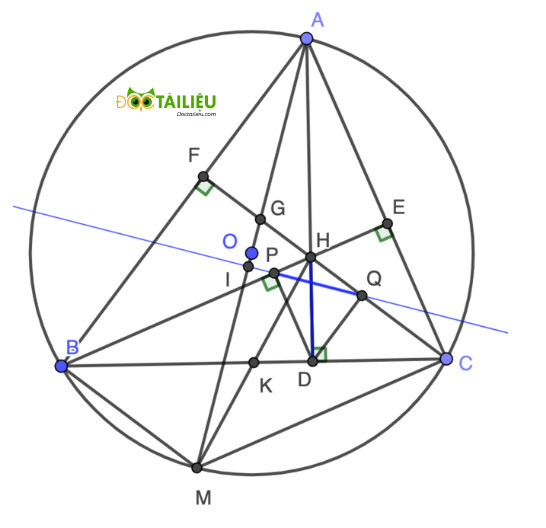
a, Chứng minh các tứ giác BCEF, AEHF nội tiếp.
Ta có BE, CF lần lượt là đường cao của tam giác ABC hay
\(\angle BFC = \angle BEC = 90⁰\)
Vậy F và E cùng nằm trên đường tròn đường kính BC, hay 4 điểm B C E F nội tiếp hay tứ giác BCEF nội tiếp (đpcm).
Tương tự ta có:
\(\angle AFH = \angle AEH = 90⁰\)
Suy ra F và E cùng nằm trên đường tròn đường kính AH, hay 4 điểm A E H F nội tiếp hay tứ giác AEHF nội tiếp (đpcm).
b,
Ta có \(\angle ACM=90⁰\) (do góc nội tiếp chắn đường kính AM)
hay AC ⊥ CM, mà lại có AC ⊥ BE, suy ra CM // BE hay CM // BH (1).
Tương tự, ta có \(\angle MBA =\angle CFA =90⁰\) suy ra BM // CF hay BM // CH (2).
Từ (1) và (2) ta có BMCH là hình bình hành (đpcm).
Gọi BC cắt CH tại K, theo tính chất hình bình hành, ta có K là trung điểm của BC và MH ⇒ OK ⊥ BC.
Xét tam giác OBK vuông tại K, ta có:
\(OK = \sqrt {OB^2 - BK^2}\)
\(= \sqrt {R^2 - \big(\frac{BC}{2}\big)^2}\)\(= \sqrt {R^2 - \big(\frac{R\sqrt3}{2}\big)^2}\) \(= \sqrt {R^2 - \frac{3R^2}{4}}\) \(= \frac{R}{2}\)
Xét tam giác AMH, có O là trung điểm AM, K là trung điểm MH ⇒ OK là đường trung bình hay \(OK = \frac{1}{2}AH\)
\(\Leftrightarrow AH = 2 . OK = R\).
Vậy \(AH =R\).
c,
Gọi AM cắt CF tại G, PQ vuông góc với AM tại I.
Xét 2 tam giác GFA và GIQ, ta có:
\(\left\{ \matrix{ \angle FGA = \angle IGQ \hfill \cr \angle AFG = \angle QIG = 90⁰ \hfill \cr} \right.\) \(\Rightarrow \triangle GFA = \triangle GIQ\)
\(\Rightarrow \angle FAG = \angle GQI\) hay \(\angle BAM = \angle HQP\).
Ta lại có:
\(\angle BAM = 90⁰ - \angle BMA \) \(= 90⁰ - \angle ACB \) (góc nội tiếp cùng chắn cung AB)
\(= \angle EBC \) \(= \angle HBD \) \(= 90⁰ - \angle BHD \) \(= \angle HDP \).
Suy ra \( \angle HDP = \angle HQP \) (do cùng \(=\angle BAM \))
hay tứ giác DPHQ nội tiếp (tính chất góc nội tiếp cùng chắn cung PH).
Mà ta có \(\angle HPD = 90⁰ \) \(\Rightarrow\) HD là đường kính của đường tròn nội tiếp tứ giác DPHQ, mà PQ là 1 dây cung của đường tròn này \(\Rightarrow\) PQ ≤ HD (đpcm).
Dấu bằng xảy ra \(\Leftrightarrow \) PQ là đường kính hay \(\angle PHQ = 90⁰ \)
\(\Leftrightarrow \angle FHE = 90⁰ = 180⁰ - \angle FAE\)
\(\Leftrightarrow \angle FAE = 90⁰\)
hay BA ⊥ AC (vô lý do tam giác ABC nhọn).
Vậy PQ < HD (dấu bằng không xảy ra).
Bài 5. (0,5 điểm)
Cho a, b là các số thực dương làm cho phương trình sau có nghiệm:
\(x^2-2(a-2b)x+a^2+b^2=0\)
Để phương trình trên có nghiệm:
\(\Leftrightarrow \Delta ' = (a-2b)^2-a^2-b^2 \geq 0\)
\(\Leftrightarrow \Delta ' = a^2-4ab+4b^2-a^2-b^2 \geq 0\)
\(\Leftrightarrow \Delta ' = 3b^2-4ab \geq 0\)
vì a, b là các số thực dương, suy ra:
\(\Delta ' = 3b^2-4ab \geq 0\) \(\Leftrightarrow 3b-4a \geq 0\) \(\Leftrightarrow \dfrac{3}{4} \geq \dfrac{a}{b}\)
Đặt \(\dfrac{a}{b}=x\), ta có:
\(0\leq x \leq \dfrac{3}{4}\) (do a;b dương)
Chia cả tử và mẫu của P cho \(b^2\), ta có:
\(P = \dfrac{ab}{a^2-2ab+3b^2}\)
\(= \dfrac{\frac{a}{b}}{\frac{a^2}{b^2}-2\frac{a}{b}+3}\)
\(= \dfrac{x}{x^2-2x+3}\)
Ta đặt:
\(f(x)= \dfrac{x}{x^2-2x+3}\)
Ta đi chứng minh nếu có \(x_1 \geq x_2\)
\(\Leftrightarrow f(x_1) \geq f(x_2)\) với \(0\leq x \leq \dfrac{3}{4}\).
Thật vậy, ta giả sử \(x_1 \geq x_2\).
Có:
\(f(x_1)-f(x_2)= \dfrac{x_1}{x_1^2-2x_1+3} - \dfrac{x_2}{x_2^2-2x_2+3}\)
\(= \dfrac{x_1(x_2^2-2x_2+3)-x_2(x_1^2-2x_1+3)}{(x_1^2-2x_1+3)(x_2^2-2x_2+3)}\)
\(= \dfrac{x_1x_2^2-2x_1.x_2+3x_1-x_2x_1^2+2x_1x_2-3x_2}{(x_1^2-2x_1+3)(x_2^2-2x_2+3)}\)
\(= \dfrac{x_1x_2(x_2-x_1)+3(x_1-x_2)}{[(x_1^2-1)^2+2][(x_2^2-1)^2+2]}\)
\(= \dfrac{(3-x_1x_2)(x_1-x_2)}{[(x_1^2-1)^2+2][(x_2^2-1)^2+2]}\)
Vì \(0\leq x \leq \dfrac{3}{4}\) \(\Rightarrow x_1x_2 \leq \dfrac{9}{16} < 3\)
\(\Leftrightarrow 3- x_1x_2 > 0\) \(\Leftrightarrow (3- x_1x_2)(x_1-x_2) \geq 0\)
Mặt khác ta có
\({[(x_1^2-1)^2+2][(x_2^2-1)^2+2]} >0\) với mọi \(x_1;x_2\)
hay tức là:
\(f(x_1)-f(x_2)=\dfrac{(3-x_1x_2)(x_1-x_2)}{[(x_1^2-1)^2+2][(x_2^2-1)^2+2]}\) \(\geq 0\) (đpcm)
Áp dụng bổ đề trên, ta có: \(0\leq x \leq \dfrac{3}{4}\) \(\Rightarrow f(x) \leq f(\frac{3}{4})\)
\(\Leftrightarrow f(x) \leq \dfrac{3/4}{(3/4)^2-2.3/4+3}\) \(=\dfrac{12}{11}\)
Tức là \(P \leq \dfrac{12}{11}\)
Dấu bằng xảy ra khi và chỉ khi \( x = \dfrac{3}{4}\) hay \(a = \dfrac{3}{4}b\).
Vậy \(Max \space P= \dfrac{12}{11}\) \(\Leftrightarrow a = \dfrac{3}{4}b\)
Trên đây là hướng dẫn giải chi tiết đề thi thử vào 10 môn toán năm 2020 trường Lương Thế Vinh lần 2, mong rằng đây sẽ là tài liệu hữu ích giúp các em ôn tập. Đừng quên còn rất nhiều tài liêu đề thi thử vào 10 môn toán khác của các tỉnh thành trên cả nước nhé.
