Trường THPT Chuyên Bến Tre sẽ tổ chức kì thi tuyển sinh vào 10 riêng với các môn chuyên, cùng tham khảo và làm quen dạng câu hỏi thi vào 10 môn Toán phát triển dựa trên đề thi năm học 2014/2015.
Cùng thử sức làm bài trong 90 phút rồi so sánh đáp án em nhé!
Đề thi thử vào 10 môn Toán năm 2020
Câu 1: (2,5 điểm)
a) Rút gọn biểu thức sau
\(A=\sqrt{\dfrac{3\sqrt{3}-4}{2\sqrt{3}+1}} - \sqrt{\dfrac{\sqrt{3}+4}{5-2\sqrt{3}}}\)
b) Cho biểu thức:
\(B=(\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1} - \dfrac{\sqrt{x}-2}{x-1})(x+\sqrt{x})\) với \(x > 0, x ≠ 1\)
i) Rút gọn biểu thức B
ii) Tìm các giá trị nguyên của x để B nhận giá trị nguyên
Câu 2: (2,5 điểm)
Cho hệ phương trình \(\left\{ \matrix{ mx+2y = 1 \hfill \cr 3x + (m+1)y = -1 \hfill \cr} \right.\)với m là tham số.
a) Giải hệ với m = 3.
b) Giải và biện luận hệ theo m.
c) Tìm m nguyên để hệ có nghiệm là số nguyên.
Câu 3: (2 điểm)
Cho phương trình bậc hai: \(x^2-mx + m - 1 = 0\)(1), với m là tham số.
i) Giải phương trình (1) khi m = 4
ii) Tìm các giá trị của m để phương trình (1) có hai nghiệm \(x_1 ; x_ 2\) thỏa mãn hệ thức
\(\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{x_1+x_ 2}{2020}\)
Câu 4: (3 điểm)
Cho tam giác đều ABC nội tiếp đường tròn đường kính AD.Gọi M là một điểm di động trên cung nhỏ AB (M không trùng với các điểm A và B).
a) Chứng minh MD là đường phân giác của góc BMC
b) Cho AD=2R.Tính diện tích của tứ giác ABDC theo R
c) Gọi O là tâm đường tròn đường kính AD.Hãy tính diện tích hình viên phân giới hạn bởi cung AMB và dây AB theo R.
d) Gọi K là giao điểm của AB và MD,H là giao điểm của AD và MC.Chứng minh ba đường thẳng AM,BD,HK đồng quy.
- Đề thi thử vào 10 môn Toán 2020 - Bến Tre -
Đáp án đề thi thử vào 10 môn Toán của trường THPT Chuyên Bến Tre năm 2020
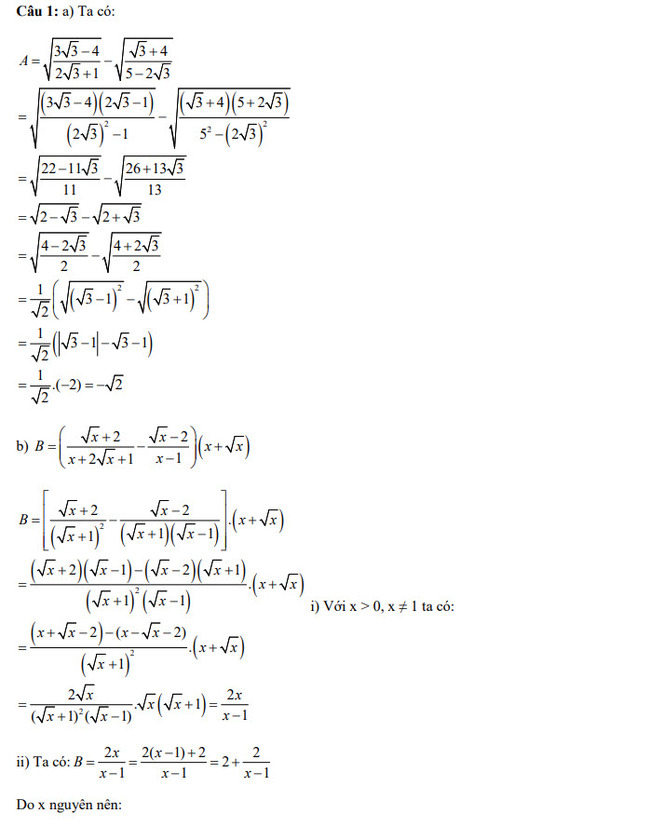

Câu 3:
a) \(x^2-mx + m - 1 = 0(1)\)
i) Với m = 4, phương trình (1) trở thành
\(x^2-4x + 3 = 0 ⇔ (x-1)(x-3)=0 \)⇔ x = 1 hoặc x = 3
Vậy tập nghiệm của (1) là {1;3}
ii) Phương trình (1) có hai nghiệm \(x_1 ; x_ 2\)
⇔\(△=m^2 - 4(m-1)≥0\)
⇔\(m^2-4m+4≥0\)
⇔\((m-2)^2≥0\)(luôn đúng ∀m)
Khi đó, theo định lý Vi–ét: \(\left\{ \matrix{ x_1 + x_ 2 = m \hfill \cr x_1x_ 2 = m-1 \hfill \cr} \right.\)
Ta có
\(\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{x_1+x_ 2}{2020}\)
⇔\(\dfrac{x_1 + x_ 2}{x_1x_2}=\dfrac{x_1+x_ 2}{2020}\)
⇔\(\dfrac{2020(x_1+x_ 2)-(x_1+x_ 2)x_1x_2}{2020x_1x_2}\)
⇔\(\dfrac{(x_1+x_ 2)-(2020-x_1x_2)}{2020x_1x_2}\)
⇔\(\left[ \begin{align}& x_1 + x_ 2 = 0 \\& x_1x_ 2 = 2020 \\\end{align} \right.\\\)
⇔ \(\left[ \begin{align}& m=0 \\& m-1=2020 \\\end{align} \right.\\\)
⇔ \(\left[ \begin{align}& m=0 \\& m=2021 \\\end{align} \right.\\\)
Vậy m ∈ {0;2021} là giá trị cần tìm
Câu 4:
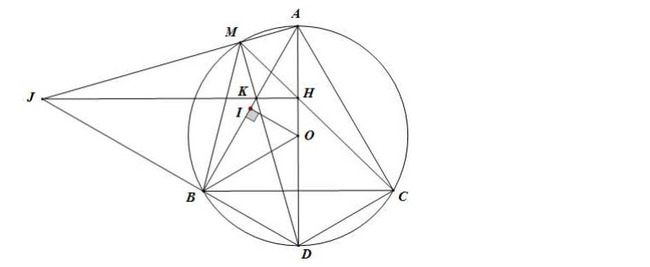
a) Vì B và C thuộc đường tròn đường kính AD nên ∠ABD = ∠ACD = 90⁰
Xét hai tam giác vuông ABD và ACD có chung cạnh huyền AD, hai cạnh góc vuông AB và AC bằng nhau (do ∆ ABC đều)
⇒ ∆ ABD = ∆ ACD (cạnh huyền – cạnh góc vuông) ⇒ ∠BAD = ∠CAD (1)
Vì AMBD là tứ giác nội tiếp nên: ∠BMD = ∠BAD (2)
Vì AMDC là tứ giác nội tiếp nên: ∠CMD = ∠CAD (3)
Từ (1), (2) và (3) => ∠BMD = ∠CMD
⇒ MD là phân giác của góc BMC.
b) Ta có: ∠BAD = ∠CAD = ∠BAC =30⁰
Xét ∆ ABD vuông tại B có: \(BA = AD.cos∠BAD = 2R.cos30⁰=R\sqrt{2}\)
Vì ABC là tam giác đều nên \(BC = BA = R\sqrt{3}\)
Vì AB = AC, DB = DC nên AD là trung trực của BC
⇒ AD ⊥ BC.
Tứ giác ABDC có AD ⊥ BC nên
\(S_{ABCD} = \dfrac{1}{2}AD.BC = \dfrac{1}{2}.2R.R\sqrt{3}=R^2\sqrt{3}\)
c) Vẽ OI ⊥ AB tại I. Xét tam giác vuông OIA ta có:
\(O1 = OA.sin∠OAI = Rsin30⁰=\dfrac{R}{2}\)
⇒ Diện tích tam giác AOB là
\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}S_{AOB}=\dfrac{1}{2}AB.OI=\dfrac{1}{2}.R\sqrt{3}.\dfrac{R}{2} = \dfrac{R^2\sqrt{3}}{4}\) (đvdt)
Ta có: ∠AOB = 2∠AOC = 120⁰ (góc ở tâm và góc nội tiếp cùng chắn cung AB)
Diện tích hình quạt AOB là
\(\dfrac{\pi R^2.120}{360}= \dfrac{\pi R^2}{3}\) (đvdt)
Suy ra diện tích hình viên phân cần tìm là
\(\dfrac{\pi R^2}{3} - \dfrac{R^2\sqrt{3}}{4} = \dfrac{R^2(4\pi-3\sqrt{3}}{12}\)(đvdt)
d) Gọi J là giao điểm của AM và BD.
Vì M , B thuộc đường tròn đường kính AD nên DM ⊥ AJ, AB ⊥ DJ
⇒ K là trực tâm của tam giác AJD
⇒ JK ⊥ AD
⇒ JK // BC (cùng ⊥ AD) (4)
Tứ giác AMKH có KMH = KAH (=BMD) nên là tứ giác nội tiếp
⇒ ∠KHA = 180⁰ – ∠KMA = 180⁰ – 90⁰ = 90⁰
⇒ KH ⊥ AD
⇒ KH // BC (cùng ⊥ AD) (5)
Từ (4) và (5), theo tiên đề Ơ–clít về đường thẳng song song, ta có J, K, H thẳng hàng.
Vậy AM, BD và KH đồng quy tại J.
Hết
Trên đây là giải chi tiết đề thi thử vào lớp 10 của trường THPT Chuyên Bến Tre đừng quên tham khảo thêm đề thi thử vào 10 các môn khác nữa em nhé!
