Cùng Đọc tài liệu thử sức với đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2021 - 2022 trường Thịnh Quang (Hà Nội):
Đề thi thử
Bài 1: ( 2 điểm) Vói \(x \geq 0, x \neq 9\) cho hai biểu thức
\(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
và \(B=\dfrac{2 \sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-3}-\dfrac{3 x+3}{x-9}\)a) Tính giá trị của biều thức A khi \(x=\dfrac{25}{16}\)
b) Rút gọn biểu thức B
c) Tim các giá trị của x để \(\dfrac{B}{A}<\dfrac{-1}{3}\)
Bài 2: (2 điểm) Một mảnh đất hình chữ nhật có chu vi 80m. Nếu tăng chiều dài thêm 3m, tăng chiều rộng thêm 5m thì diện tích của mảnh đất tăng thêm 195m². Tính chiều dài và chiều rộng của mẳnh đất.
Bài 3: (2 diểm)
1. Giäi hệ phưng trình sau:
\(\left\{\begin{array}{l}2 \sqrt{x-2}+3 \sqrt{y-3}=14 \\ \sqrt{x-2}+\sqrt{y-3}=5\end{array}\right.\)
2. Cho hệ phưong trình :
\(\left\{ \matrix{ -2 m x+y=5 \hfill \cr m x+3 y = 1 \hfill \cr} \right. (1) \)
Xác định giá trị của m đề hệ (1) có nghiệm duy nhất (x, y) thỏa mãn: x - y = 2
Bài 4. (3,5 điểm) Cho đường tròn (O; R) đường kính AB. Kè tiếp tuyến Ax và lấy trên tiếp tuyến đó một điểm P sao cho AP> R. Từ P kẻ tiếp tuyến tiếp xúc với (O) tại M.
a) Chứng minh rằng 4 điểm A, P, M, O cùng nằm trên một đường tròn.
b) Chúng minh BM // OP.
c) Đường thằng vuông góc với AB ờ O} cắt tia BM tai N. Chứng minh tứ giác OBNP là hình bình hành.
d) Biết AN cắt OP tại K, PM cắt ON tai I, PN và OM kéo dài cắt nhau tại J. Chứng minh 3 điểm I, J, K thẳng hàng.
Bài 5 (0,5 điểm) Giải phương trình: \(x^{2}+4 x+7=(x+4) \sqrt{x^{2}+7}\)
Hết
Vậy là cấu trúc đề thi thử vào lớp 10 môn Toán của trường THCS Thịnh Quang đều không có nhiều thay đổi so với cấu trúc đề tuyển sinh vào lớp 10 các năm. Hãy thử sức làm bài trong thời gian 120 phút rồi so sánh đối chiếu với lời giải chi tiết dưới đây sau em nhé.
Đáp án đề thi thử vào lớp 10 môn Toán
Bài 1: ( 2 điểm)
a) Với \(x=\dfrac{25}{16}\) ta có:
\(A=\dfrac{\dfrac{5}4+1}{\dfrac{5}4-3}\) \(=\dfrac{-9}{7}\)
b) Với \(x \geq 0, x \neq 9\) ta có:
\(B=\dfrac{2 \sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-3}-\dfrac{3 x+3}{x-9}\)
\(=\dfrac{2 \sqrt{x}(\sqrt{x}-3) + \sqrt{x}(\sqrt{x}+3) - 3x -3 }{(\sqrt{x}+3)(\sqrt{x}-3)}\)
\(=\dfrac{-3\sqrt{x} - 3}{(\sqrt{x}+3)(\sqrt{x}-3)}\)
\(=\dfrac{-3(\sqrt{x} + 1)}{(\sqrt{x}+3)(\sqrt{x}-3)}\)c) Với \(x \geq 0, x \neq 9\) ta có:
\(\dfrac{B}{A} =\dfrac{-3(\sqrt{x} + 1)}{(\sqrt{x}+3)(\sqrt{x}-3)} :\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\) \( =\dfrac{-3}{\sqrt{x}+3} \)
Để \(\dfrac{B}{A}<\dfrac{-1}{3}\) tương đương với:
\(\dfrac{-3}{\sqrt{x}+3} < \dfrac{-1}3\)
\(\Leftrightarrow \dfrac{3}{\sqrt{x}+3} > \dfrac{1}3 \text{ vì } \sqrt{x} + 3 >0\)
\(\Leftrightarrow \sqrt{x}+3 < 9 \)
\(\Leftrightarrow \sqrt{x} < 6\)
\(\Leftrightarrow 0 \leq x < 36, x \neq 9\)
KL...
Bài 2: (2 điểm)
Gọi chiều dài và chiều rộng mảnh đất lần lượt là X và Y (mét; X, Y > 0)
Theo bài ra ta có:
\(\left\{\begin{array}{l} 2(X+Y) = 80 \\(X+3)(Y+5) - XY = 195\end{array}\right.\)
\(\Leftrightarrow \left\{\begin{array}{l} X+Y = 40 \\5X + 3Y + 15 = 195\end{array}\right.\)
\(\Leftrightarrow \left\{\begin{array}{l} X+Y = 40 \\5X + 3Y = 180\end{array}\right.\)
\(\Leftrightarrow \left\{\begin{array}{l} X=30 \text{ (m)} \\Y = 10 \text{ (m)}\end{array}\right.\)
(tm)KL...
Bài 3: (2 diểm)
1.
ĐKXĐ: \(x \geq 2; y\geq 3\). Ta có:
\(\left\{\begin{array}{l}2 \sqrt{x-2}+3 \sqrt{y-3}=14 \\ \sqrt{x-2}+\sqrt{y-3}=5\end{array}\right.\)
\(\Leftrightarrow \left\{\begin{array}{l}\sqrt{x-2}=1 \\ \sqrt{y-3}=4\end{array}\right.\)
\(\Leftrightarrow \left\{\begin{array}{l}x-2=1 \\ y-3=16\end{array}\right.\)
\(\Leftrightarrow \left\{\begin{array}{l}x=3 \\ y=19\end{array}\right.\) (tm)
KL....
2.
Để hệ (1) có nghiệm duy nhất (x, y) thỏa mãn: x - y = 2 ta có:
\(\Leftrightarrow \left\{ \matrix{ -2 m x+y=5 \hfill \cr 2m x+6 y = 2\hfill \cr x-y = 2\hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{ -2 m x+y=5 \hfill \cr 7y = 7\hfill \cr x-y = 2\hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{ -2 m x+y=5 \hfill \cr y = 1 \hfill \cr x = 3 \hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{ -2 m .3+1=5 \hfill \cr y = 1 \hfill \cr x = 3 \hfill \cr} \right. \)
\(\Rightarrow m = \dfrac{-2}{3}\)
KL....
Bài 4. (3,5 điểm)
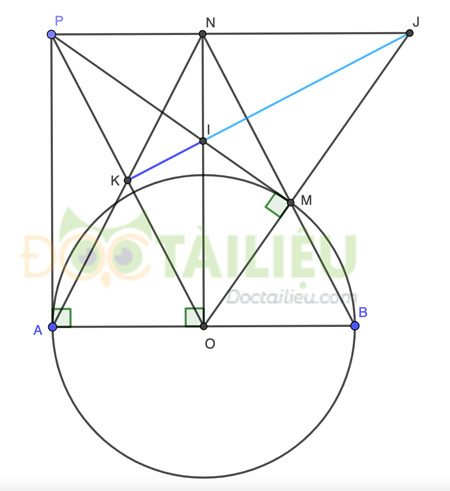
a)
Vì PA, PM là tiếp tuyến lần lượt tại A và M của (O) nên ∠PAO = ∠PMO = 90°
Suy ra A và M cùng thuộc đường tròn đường kính PO hay 4 điểm A, P, M, O cùng nằm trên một đường tròn (đpcm).
b)
Dễ chứng minh △OAP = △OMP (cạnh huyền - cạnh góc vuông) ⇒ \(∠POA = ∠POM =\dfrac{∠AOM}{2}\)
Lại có \(∠ABM =\dfrac{∠AOM}{2} = ∠AOP\) ⇒ BM // OP (đồng vị) (đpcm).
c)
Xét △ANB có NO là trung trực ⇒ △ANB cân tại N ⇒ ∠ONA = ∠BNO = 90° - ∠NBA = 90° - ∠POA = ∠OPA
⇒ ONPA là hình chữ nhật ⇒ PN // OA hay PN // OB hay tứ giác OBNP là hình bình hành (đpcm)
d) Biết AN cắt OP tại K, PM cắt ON tai I, PN và OM kéo dài cắt nhau tại J. Chứng minh 3 điểm I, J, K thẳng hàng.
Xét △PJO có PM ⊥ OJ, ON ⊥ PJ và PM cắt ON tại I hay I là trực tâm của △PJO ⇒ JI ⊥ PO (1)
Lại có AONP là hình chữ nhật ⇒ ∠OPN = ∠POA = ∠POM hay △PJO cân tại J, có K là trung điểm PO suy ra JK ⊥ PO (2)
Từ (1) và (2) suy ra 3 điểm I, J, K thẳng hàng (đpcm)
Bài 5 (0,5 điểm)
Ta có:
\(x^{2}+4 x+7=(x+4) \sqrt{x^{2}+7}\) (1)
\(\Leftrightarrow (x+2)^2 + 3=(x+4) \sqrt{x^{2}+7} \geq 3 > 0\)
\(\Rightarrow x+4 > 0 \Leftrightarrow x > -4\)
Với x > -4 ta có:
(1) \(\Leftrightarrow (x^2+4x + 7)^2=(x+4)^2 (x^2+7)\)
\(\Leftrightarrow x^4 + 16x^2 + 49 + 8x^3 + 14x^2 + 56 x=(x^2+8x + 16)(x^2+7)\)
\(\Leftrightarrow x^4 +8x^3 + 30x^2 + 56 x + 49 =x^4 + 8x^3 + 23 x^2 + 56x + 112\)
\(\Leftrightarrow 7x^2 - 63 = 0\)
\(\Leftrightarrow x^2 = 9\)
\(\Leftrightarrow \left[\matrix{ x = 3 \hfill \cr x = -3 \hfill \cr} \right.\) (tm đkxđ)
KL....
Trên đây là lời giải chi tiết đề thi thử vào 10 môn toán năm 2021 lần 1 của THCS Thịnh Quang, mong rằng đây sẽ là tài liệu hữu ích giúp các em ôn tập. Đừng quên còn rất nhiều tài liêu đề thi thử vào lớp 10 môn toán khác của các tỉnh thành trên cả nước nhé.
