Cùng Đọc tài liệu thử sức với đề thi thử vào lớp 10 môn toán năm 2020-2021 của Sở Giáo dục và đào tạo tỉnh Nam Định để chuẩn bị tốt nhất cho kỳ thi vào 10 sắp tới.
Đề tham khảo tuyển sinh vào 10 2021 môn toán sở GD Nam Định
Phần I: Trắc nghiệm (2,0 điểm).
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước phương án đổ vào bài làm.
Câu 1: Tìm điều kiện để biểu thức có nghĩa \(3\sqrt{1-x}+\sqrt{x+1}\)
A. \(-1\leq x\leq 1\)
B. \(x\geq -1\)
C. \(x\leq 1\)
D. \(x\leq -1 hoặc x\geq 1\)
Câu 2: Trong các hàm số sau, hàm số nào nghịch biến trên R?
A. \(y=x^2\)
B. \(y=x(\sqrt{2}+1)+2021 \)
C. \(y=\frac{-1}{2}x^2 \)
D. \(y=(1-\sqrt{2})x+2021\)
Câu 3: Hệ phương trình \(\left\{\begin{array}{l} -x+5 y=6 \\ x+2 y=1 \end{array}\right.\) có nghiệm (x; y) là
A. (2;1)
B. (1;2)
C. (1;1)
D. (-1;-1).
Câu 4: Điểm nào sau đây thuộc đồ thị hàm số \(y = -2x^2\)
A. (-1:2).
B. (1:2).
c. (-1-2).
D. (2:-1).
Câu 5: Trong các phương trình sau, phương trình nào có tổng hai nghiệm bằng 2?
A. \(x^{2}-2x+2=0\)
B. \(x^{2}-3x+2=0\)
C. \(x^{2}-2=0\)
D. \(\sqrt{2022} x^{2}-2 \sqrt{2022} x-4=0\) .
Câu 6: Cho tam giác ABC vuông tại A, biết AB = 3cm, AC = 4cm. Tính độ dài đường cao AH.
A. 12/5cm
B. 5cm
C. 5/12cm
D. 7cm
Câu 7: Một tam giác vuông cân có độ dài cạnh góc vuông là \(3\sqrt{2}\)cm, khi đó bán kính đường tròn ngoại tiếp tam giác đó bằng
A. 6 cm
B. 3 cm.
C. \(\sqrt{2}\) cm.
D. \(\frac{\sqrt{2}}{2}\) cm
Câu 8: Một bóng đèn huỳnh quang dài 1,2m đường kính của đường tròn đáy là 4cm, được đặt khít vào một ống giấy cứng dạng hình hộp (như hình vẽ dưới đây). Tính diện tích phần giấy cần dùng để làm một hộp (biết hộp hở hai đầu, không tính lề và mép dán).
A. \(1920 cm^2\)
B. \(1920 dm^2\)
C. \(1920 m^2\).
D. \(192 dm^2\)
Phần II: Tự luận (8,0 điểm)
Bài 1. (1,5 điểm) Cho hai biểu thức \(A=\frac{6-\sqrt{x}}{6-2 \sqrt{x}} \) và \(B=\frac{2 \sqrt{x}-12}{x-2 \sqrt{x}-3}+\frac{\sqrt{x}}{2 \sqrt{x}+2}\)
1) Tính giá trị biểu thức A khi x = 16,
2) Rút gọn biểu thức P = B - A.
Bài 2. (1.5 điểm)
1) Tìm tọa độ giao điểm của đường thẳng (d) \(y = 2x+3\) và parabol (P) \(y =x^2\).
2) Cho phương trình \(x^2 - 2mx-1=0\) (với m là tham số), Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt \(x_1, x_2 ( x_1>x_2)\), thỏa mãn \(\left |x_1 \right |-\left | x_2 \right |+\left | x_1x_2 \right |=m+3\).
Bài 3. (1,0 điểm) Giải hệ phương trình sau: \(\left\{\begin{matrix} \sqrt{xy-1}(\sqrt{xy-1}+5)=6\\ x(y+1)=4\end{matrix}\right.\)
Bài 4. (3,0 điểm)
1) Cho tam giác ABC vuông tại A có độ dài các cạnh AB = 6cm, AC = 3cm. Lấy điểm M trên cạnh AB sao cho nửa đường tròn (O) đường kính AM tiếp xúc với cạnh BC tại N. Tính diện tích phần tam giác ABC nằm ngoài nửa hình tròn (O) (phần tô đậm trong hình về bên, kết quả làm tròn đến số thập phân thứ nhất).
2) Cho tam giác ABC vuông tại A, M là một điểm thuộc cạnh AC ( M khác A và C). Đường tròn đường kính MC cắt BC tại N và cắt tỉa BM tại I. Chứng minh rằng:
a) ABNM và ABCI là các tứ giác nội tiếp đường tròn.
b) Gọi K là giao điểm của NI và MC. Chứng minh: \(\frac{MA}{AC}=\frac{MK}{CK}\)
Bài 5. (1,0 điểm)
1) Giải phương trình \(\sqrt{3 x+4+\sqrt{x+3}}=1+2 \sqrt{x+3}-\sqrt{3 x+3-\sqrt{x+3}}\).
2) Xét ba số dương a,b,c thỏa mãn abc= 1. Tìm giá trị nhỏ nhất của biểu thức
\(P=\frac{b^{2}}{a}+\frac{c^{2}}{b}+\frac{a^{2}}{c}+\frac{9}{2(a b+b c+c a)}\)
-Hết-
Đáp án đề tham khảo tuyển sinh vào 10 môn toán 2021 sở GD Nam Định
Phần I: Trắc nghiệm
1 - A
2 - D
3 - D
4 - C
5 - D
6 - A
7 - B
8 - A
Phần II: Tự luận
Bài 1.
1)
Với x = 16 (thỏa đkxđ), ta có:
\(A=\dfrac{6-\sqrt{16}}{6-2 \sqrt{16}} =\dfrac{6-4}{6-2 \times4} = -1 \)
KL...
2)
ĐKXĐ: \(x \geq0;x ≠ 9\), ta có:
\(P= B-A =\dfrac{2 \sqrt{x}-12}{x-2 \sqrt{x}-3}+\dfrac{\sqrt{x}}{2 \sqrt{x}+2} - \dfrac{6-\sqrt{x}}{6-2 \sqrt{x}} \)
\( =\dfrac{2 \sqrt{x}-12}{(\sqrt{x}-3)(\sqrt{x}+1)}+\dfrac{\sqrt{x}}{2( \sqrt{x}+1)} - \dfrac{6-\sqrt{x}}{2(3- \sqrt{x})} \)
\( =\dfrac{4 \sqrt{x}-24 + \sqrt{x}( \sqrt{x}-3) + (6- \sqrt{x})( \sqrt{x}+1) }{2(\sqrt{x}-3)(\sqrt{x}+1)}\)
\( =\dfrac{4 \sqrt{x}-24 + x - 3 \sqrt{x} - x + 5 \sqrt{x} + 6 }{2(\sqrt{x}-3)(\sqrt{x}+1)}\)
\( =\dfrac{6\sqrt{x} - 18 }{2(\sqrt{x}-3)(\sqrt{x}+1)}\)
\( =\dfrac{3 }{\sqrt{x}+1}\)
KL....
Bài 2.
1) Tìm tọa độ giao điểm của đường thẳng (d) \(y = 2x+3\) và parabol (P) \(y =x^2\).
Xét PT hoành độ giao điểm của (d) và (P) ta có:
\(x^2 = 2x + 3\)
\(\Leftrightarrow x^2 - 2x - 3 = 0\)
\(\Leftrightarrow (x-3)(x+1)= 0\)
\(\Leftrightarrow \left[ \matrix{ x = 3 \Rightarrow y = 9 \hfill \cr x = -1 \Rightarrow y = 1 \hfill \cr} \right.\)
KL....
2) Cho phương trình \(x^2 - 2mx-1=0\) (với m là tham số), Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt \(x_1, x_2 ( x_1>x_2)\), thỏa mãn \(\left |x_1 \right |-\left | x_2 \right |+\left | x_1x_2 \right |=m+3\).
Để phương trình đã cho có 2 nghiệm phân biệt ⇔
\(\Delta' = m^2 + 1> 0\) (luôn đúng với mọi m)
Suy ra phương trình đã cho luôn có hai nghiệm phân biệt.
Áp dụng hệ thức Vi-ét cho PT đã cho, ta có:
\(\left\{\begin{matrix} x_1+x_2 = 2m \\ x_1x_2 = -1 \end{matrix}\right.\)
Vì \(x_1x_2 = -1 < 0 \) ⇔ \(x_1;x_2\) trái dấu, mà \(x_1>x_2\) ⇔ \(x_1> 0 > x_2\)
Thay vào ta có:
\(\left |x_1 \right |-\left | x_2 \right |+\left | x_1x_2 \right |=m+3\)
\(\Leftrightarrow x_1+x_2+\left | -1 \right |=m+3\)
\(\Leftrightarrow 2m=m+2\)
\(\Leftrightarrow m =2 \) (thỏa mãn)
KL....
Bài 3. (1,0 điểm) Giải hệ phương trình sau: \(\left\{\begin{matrix} \sqrt{xy-1}(\sqrt{xy-1}+5)=6\\ x(y+1)=4\end{matrix}\right.\)
ĐKXĐ: xy ≥ 1
Ta có hệ đã cho tương đương với:
\(\left\{\begin{matrix} (\sqrt{xy-1})^2 + 5\sqrt{xy-1} - 6 = 0 \\ x(y+1) = 4 \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} (\sqrt{xy-1}+6)(\sqrt{xy-1} - 1) = 0 \\ x(y+1) = 4 \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} \sqrt{xy-1} - 1= 0 \text{ (vì }\sqrt{xy-1} \geq 0 ) \\ xy + x = 4 \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} xy = 2 \\ xy + x = 4 \Rightarrow x = 2 \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x= 2 \\ y = 1 \end{matrix}\right.\) (thỏa mãn đkxđ)
KL....
Bài 4.
1.
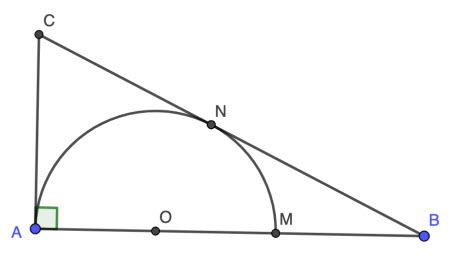
Vì OM ⊥ BC nên OC là phân giác ∠ACB.
\(\Rightarrow \quad \dfrac{A O}{A C}=\dfrac{O B}{B C}=\dfrac{A B}{A C+B C} \)
\(\Rightarrow A O=A C \cdot \dfrac{A B}{A C+B C}=\dfrac{3.6}{3+3 \sqrt{5}}=\dfrac{3}{2}(\sqrt{5}-1)\)
\(\Rightarrow S=S_{A B C}-\dfrac{1}{2} A O^{2} \cdot \pi \)
\(=\dfrac{3.6}{2}-\dfrac{1}{2} \cdot \dfrac{9}{4}(\sqrt{5}-1)^{2} \cdot \pi \approx 3,60\)
2.
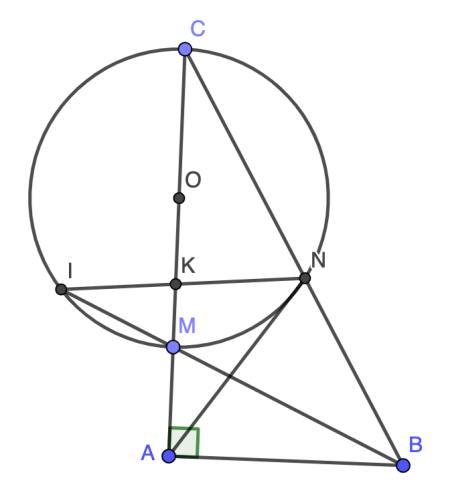
a) ABNM và ABCI là các tứ giác nội tiếp đường tròn. (dễ CM)
b) Gọi K là giao điểm của NI và MC. Chứng minh: \(\frac{MA}{AC}=\frac{MK}{CK}\)
AMNB nội tiếp => \(\widehat{OAN} = \widehat{IBN}\)
\(\widehat{O N K}=\frac{180-I \widehat{O N}}{2}=90^{\circ}+\widehat{BCI}\)
\(\Rightarrow \widehat{ON K}= \widehat{OAN} \Rightarrow △ONK ∽ △OAN\)
\(\Rightarrow \dfrac{O K}{O N}=\frac{O N}{O A} \Rightarrow O N^{2}=O K . O A \)
\(\Rightarrow 2ON^{2}=2OK.O A \)
\(\Rightarrow O N \cdot(2ON)=O K \cdot(2 OA) \Rightarrow O N \cdot(A C-M A)=OK(A C+A M) \)
\(\Rightarrow A C(O N-OK)=A M(O K+O N) \)
\(\Rightarrow A C(O M-O K)=A M(O K+O C) \)
\(\Rightarrow A C \cdot M K=A M . KC\)
\(\Rightarrow \dfrac{A M}{A C}=\dfrac{K M}{K C}\)=> đpcm
Bài 5.
1) Giải phương trình \(\sqrt{3 x+4+\sqrt{x+3}}=1+2 \sqrt{x+3}-\sqrt{3 x+3-\sqrt{x+3}}\) (1)
ĐKXĐ: \(x \geq -3\)
Đặt \(a =\sqrt{x+3}\) (\(a \geq 0\))
\(\Leftrightarrow x = a^2 - 3\)
Thay vào PT đã cho, ta có:
(1) \(\Leftrightarrow \sqrt{3 (a^2 - 3)+4+a}=1+2 a-\sqrt{3 (a^2 - 3)+3-a}\)
\(\Leftrightarrow \sqrt{3a^2 +a - 5}=1+2 a- \sqrt{3a^2 - a - 6}\)
\(\Leftrightarrow \sqrt{3a^2 +a - 5}+ \sqrt{3a^2 - a - 6}=1+2 a\) (2)
Xét \(\sqrt{3a^2 +a - 5}- \sqrt{3a^2 - a - 6} = 0 \Leftrightarrow 2a + 1 = 0 \) Vô lý vì \(a \geq 0\)
\(\Leftrightarrow \sqrt{3a^2 +a - 5}- \sqrt{3a^2 - a - 6} ≠ 0\). Nhân vào cả 2 vế (2), ta có:
\(\Leftrightarrow (\sqrt{3a^2 +a - 5}+ \sqrt{3a^2 - a - 6})(\sqrt{3a^2 +a - 5}- \sqrt{3a^2 - a - 6})=(1+2 a)(\sqrt{3a^2 +a - 5}- \sqrt{3a^2 - a - 6})\)
\(\Leftrightarrow 2a+1=(1+2 a)(\sqrt{3a^2 +a - 5}- \sqrt{3a^2 - a - 6})\)
\(\Leftrightarrow (1+2 a)(\sqrt{3a^2 +a - 5}- \sqrt{3a^2 - a - 6} - 1) = 0\)
\(\Leftrightarrow \left\{\begin{matrix} 2a + 1 = 0 \text { (Loại vì a ≥ 0)} \\ \sqrt{3a^2 +a - 5}- \sqrt{3a^2 - a - 6} = 1 \end{matrix}\right.\)
\(\Leftrightarrow \sqrt{3a^2 +a - 5} = \sqrt{3a^2 - a - 6} + 1\)
\(\Leftrightarrow 3a^2 +a - 5 = 3a^2 - a - 5 + 2\sqrt{3a^2 - a - 6} \)
\(\Leftrightarrow 2a = 2\sqrt{3a^2 - a - 6} \)
\(\Leftrightarrow a^2 = 3a^2 - a - 6\)
\(\Leftrightarrow 2a^2 - a - 6 = 0\) (2a + 3)(a - 2)
\(\Leftrightarrow \left[ \matrix{ a = \dfrac{-3}2 \text{ (loại vì a ≥ 0)} \hfill \cr a = 2 \hfill \cr} \right. \)
⇒ x = 1 (thỏa mãn đkxđ)
KL....
2) Xét ba số dương a,b,c thỏa mãn abc= 1. Tìm giá trị nhỏ nhất của biểu thức
\(P=\frac{b^{2}}{a}+\frac{c^{2}}{b}+\frac{a^{2}}{c}+\frac{9}{2(a b+b c+c a)}\)
Áp dụng BDT Bunhiacopxki ta có:
\(\dfrac{b^{2}}{a}+\dfrac{c^{2}}{b}+\dfrac{a^{2}}{c} \geq \dfrac{(a+b+c)^2}{a+b+c} = a+b+c\)
Áp dụng BDT Cauchy ta có:
\((a+b+c)^2 \geq 3 (ab+bc+ca)\)
\(\Leftrightarrow a+b+c \geq \sqrt{3 (ab+bc+ca)}\)
Ta có:
\(P\geq \sqrt{3(ab+bc+ca)} + \dfrac{9}{2(a b+b c+c a)}\)
\(\Leftrightarrow P\geq \dfrac{\sqrt{3(ab+bc+ca)}}{2}+ \dfrac{\sqrt{3(ab+bc+ca)}}{2}+ \dfrac{9}{2(a b+b c+c a)}\)
Áp dụng BDT Cauchy ta có:
\(\Leftrightarrow P\geq \dfrac{\sqrt{3(ab+bc+ca)}}{2}+ \dfrac{\sqrt{3(ab+bc+ca)}}{2}+ \dfrac{9}{2(a b+b c+c a)} \geq 3.\dfrac{3}2 = \dfrac{9}2\)
Vậy\({min} _P = \dfrac{9}2 \Leftrightarrow a=b=c=1\)
KL...
Trên đây là chi tiết đề thi thử vào 10 môn toán năm 2021 của sở Giáo dục Nam Định mong rằng đây sẽ là tài liệu hữu ích giúp các em ôn tập. Đừng quên còn rất nhiều tài liêu đề thi thử vào 10 môn Toán 2021 khác của các tỉnh thành trên cả nước nhé.
