Trường THCS Hoàn Kiếm (Hà Nội) vừa diễn ra kì thi khảo sát chất lượng đầu vào môn Toán dành cho học sinh lớp 9, cùng Đọc tài liệu tham khảo đề thi và lời giải chi tiết dưới đây:
Đề thi thử vào lớp 10 THCS Hoàn Kiếm 2021
Trường THCS Hoàn Kiếm - Năm học 2020 - 2021
Đề khảo sát toán 9
Thời gian làm bài 90 phút
Bài 1 (2đ): Cho 2 biểu thức
\(A=\frac{\sqrt{x}-5}{\sqrt{x}}\) và \(B=\frac{\sqrt{x}}{\sqrt{x}-5}-\frac{3 \sqrt{x}}{x-25}\) vói \(x>0, x \neq 25\)
a) Tính giá trị của biểu thức A khi x = 81
b) Cho P = A.B. Chứng minh rằng \(P=\frac{\sqrt{x}+2}{\sqrt{x}+5}\)
c) So sánh \(\sqrt{P}\) với P.
Bài 2 (2đ): Theo kế hoạch một người công nhân phải hoàn thành 84 sản phẩm trong một thời gian nhất định. Do cải tiến kĩ thuật, nên thực tế mỗi giờ người đó đã làm được nhiều hơn 2 sản phẩm so với số sản phẩm phải làm trong 1 giờ theo kế hoạch. Vì vậy, người đó đã hoàn thành công việc sớm hơn 1 giờ. Hỏi theo kế hoạch, mỗi giờ người công nhân phải làm được bao nhiêu sản phẩm?
Bài 3 (2đ)
1) Giải hệ phương trình sau:
2) Cho parabol (P): y = x^2 và đường thẳng (d): y = 2(m-1)x + m^2 + 2m (m là tham số).
a) Chứng minh rằng (d) luôn cắt (P) tại 2 điểm phân biệt với mọi m
b) Với m = 2. Vẽ (P) và (d) trên cùng 1 hệ trục tọa độ
Bằng tính toán, xác định tọa độ giao điểm của (d) và (P)
Bài 4 (3,5đ): Cho đường (O; R) và điểm A cố định nằm ngoài đường tròn. Qua A kẻ hai tiếp tuyến AM, AN tới đường tròn (M, N là hai tiếp điểm). Một đường thẳng d đi qua A cắt (O; R) tại B và C (AB < AC). Gọi I là trung điểm của BC
a) Chứng minh năm điểm A, M, N, O, I cùng thuộc một đường tròn
b) Chứng minh AM^2 = AB.AC
c) Đường thẳng qua B, song song với AM cắt MN tại E. Chứng minh rằng IE song song với MC
d) Chứng minh khi d thay đổi quanh điểm A thì trọng tâm G của tam giác MBC luôn nằm trên một đường tròn cố định
Bài 5 (0,5đ): Với a, b, c là các số dương thỏa mãn a+ b + c + ab + bc + ca = 6abc.
Chứng minh: \(\dfrac{1}{a^{2}}+\dfrac{1}{b^{2}}+\dfrac{1}{c^{2}} \geq 3 \)
Hết
Vậy là Đọc tài liệu đã giới thiệu tới các em đề thi minh họa tuyển sinh vào 10 2020 môn Toán của Hải Phòng, đừng quên còn rất nhiều tài liệu đề thi thử vào 10 khác đang đợi các em khám phá nhé!
Đáp án đề thi thử vào 10 Hoàn Kiếm 2021

Bài 2

Bài 3

Bài 4
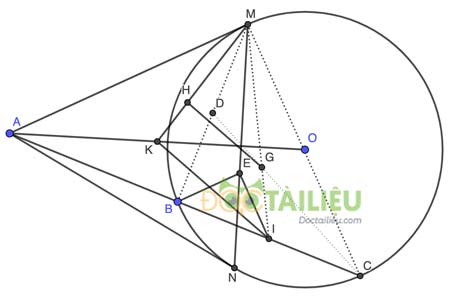
a. Cách 1: Xét (O) có: BC là dây cung
I là trung điểm BC
⇒ OI ⊥BC (tính chất)
Xét (O) có: AM;AN là các tiếp tuyến của đường tròn
⇒AM⊥OM;AN⊥ON;AM=AN
Xét tứ giác AMON có:
∠AMO =∠ANO =90⁰
⇒∠AMO +∠ANO =180⁰
⇒ Tứ giác AMON nội tiếp (tổng 2 góc đối =180⁰)
⇒ 4 điểm A;M;O;N thuộc 1 đường tròn(1)
Lại có: ∠AIO =∠ANO =90⁰
⇒∠AIO +∠ANO =180⁰
⇒ Tứ giác AION nội tiếp (Tổng 2 góc đối =180⁰)
hay 4 điểm A;I;O;N thuộc 1 đường tròn (2)
Từ (1)(2)⇒ 5 điểm A;I;O;M;N thuộc 1 đường tròn (đpcm)'
Cách 2:
Ta có : ∠ AMO = ∠ ANO = 90⁰ (t/c tiếp tuyến)
Mặt khác I là tđ BC => OI vuông góc BC (t/c đường kính và dây) => góc AIO = 90⁰
=> 5 điểm A, M, O, I, N cùng nằm trên một đường tròn
b. Xét (O) có: ∠AMB =∠ACM (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung MB)
Xét △AMB và △ACM có:
∠AMB =∠ACM
∠A chung
⇒ △AMB ∽ △ACM(g.g)
⇒\(\dfrac{AM} {AC} =\dfrac{AB} {AM }\)
Hay AB.AC=AM²
c.
Ta có ∠MAI = ∠ MNI (AMIN nt), mà ∠EBI = ∠MAI (đồng vị, do AM // BE) => ∠MNI = ∠EBI hay ∠ENI = ∠EBI
=> Tứ giác NBEI nội tiếp => ∠BNE = góc BIE. Mà ∠BNE = ∠BCM (cùng chắn cung MB trong (O))
=> ∠BIE = ∠BCM => IE // CM
d.
* Gọi K là trung điểm của AO
K cố định; \(IK=\dfrac{1}{2} OA \)không đồi
* Có: G là trọng tâm △MBC (gt)
I là trung điểm của BC (gt)=> MI là trung tuyến của △MBC (đn)
=>G thuộc MI ; \(GI=\frac{1}{3} {MI}\)
* Kè GH // IK (H thuộc MK)
Theo đl Ta lét: \(\dfrac{M H}{M K}=\dfrac{H G}{I K}=\dfrac{M G}{M I}=\dfrac{2}{3}\)
=> H cố định và \(HG =\frac{2}{3} I K=\frac{1}{3} A O\) không đồi
Vậy G thuộc đường tròn \(\left({H} ; \frac{1}{3} A O\right)\)

Vậy là Đọc tài liệu đã cung cấp thêm một mẫu đề thi thử tuyển sinh vào lớp 10 môn Toán năm học 2021/2022, đây chắc chắn là một tài liệu hữu ích giúp các em ôn luyện giải đề cũng nhưng các dạng toán có thể gặp trong kỳ thi tuyển sinh vào lớp 10 các năm. Chúc các em học tốt.
