Cùng Đọc tài liệu thử sức với đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2021 - 2022 của Tỉnh Bắc Kạn vừa ra
Đề thi thử tuyển sinh vào 10 môn toán
Câu 1. Cho biểu thức \(A=\left(\frac{2}{\sqrt{x}-2}+\frac{3}{2 \sqrt{x}+1}-\frac{5 \sqrt{x}-7}{2 x-3 \sqrt{x}-2}\right): \frac{2 \sqrt{x}+3}{5 x-10 \sqrt{x}}\)
\((x>0, x \neq 4)\)1) Rút gọn biều thức A
2) Tính giá trị cúa A khi \(x=3-2 \sqrt{2}\)
3) Tim x sao cho A nhận giá trị là một số nguyên.
Câu 2. Cho phương trình \(x^{2}-(m-1)-m^{2}+m-2=0\), vói m là tham số.
a) Chứng minh rằng phương trình đã cho có hai nghiệm trái dấu vói mọi m.
b) Gọi hai nghiệm của phương trình đã cho là \(x_{1}, x_{2}\). Tìm m để biểu thức \(A=\left(\frac{x_{1}}{x_{2}}\right)^{3}-\left(\frac{x_{2}}{x_{1}}\right)^{3}\) đạt giá trị lón nhất.
Câu 3. Một ca nô xuôi dòng 78 km và ngược dòng 44 km mất 5 giờ với vận tốc dự định. nếu ca nô xuôi 13 km và ngurợc dòng 11 km với cùng vận tốc dự định đó thì mất 1 giờ. Tính vận tốc riêng của ca nô và vận tốc dòng nước.
Câu 4. Từ điểm K nằm ngoài đường tròn (O) ta kẻ các tiếp tuyến KA, KB cát tuyến KCD đến (O) sao cho tia KC nằm giữa hai tia KA, KO. Gọi H là trung điểm CD.
a) Chứng minh: 5 điểm A, K, B, O, H cùng nằm trên một đường tròn.
b) Gọi M là trung điểm của AB. Chứng minh: Tứ giác MODC nội tiếp.
c) Đường thẳng qua H song song với BD cắt AB tại I. Chúmg minh \(C I \perp O B\).
Câu 5. Cho các số thực x, y, z thóa mãn điều kiện: \(x^{2}+y^{2}+z^{2}=2\).
Chứng minh rằng: \(x+y+z \leq x y z+2\)
Hết
Vậy là đề thi thử vào lớp 10 môn Toán năm 2021 số 1 của tỉnh Bắc Kạn đều không có thay đổi so với cấu trúc đề tuyển sinh vào lớp 10 các năm. Hãy thử sức làm bài trong thời gian 120 phút rồi so sánh đối chiếu với lời giải chi tiết dưới đây sau em nhé.
Đáp án đề thi thử vào lớp 10 môn Toán
Câu 1.
1) Với x>0, x \neq 4, ta có:
\(\begin{array}{l} A=\left(\dfrac{2}{\sqrt{x}-2}+\dfrac{3}{2 \sqrt{x}+1}-\dfrac{5 \sqrt{x}-7}{2 x-3 \sqrt{x}-2}\right): \dfrac{2 \sqrt{3}+3}{5 x-10 \sqrt{x}} \\ =\dfrac{2(2 \sqrt{x}+1)+3(\sqrt{x}-2)-(5 \sqrt{x}-7)}{(\sqrt{x}-2)(2 \sqrt{x}+1)}: \dfrac{2 \sqrt{x}+3}{5 \sqrt{x}(\sqrt{x}-2)} \\=\dfrac{2 \sqrt{x}+3}{(\sqrt{x}+2)(2 \sqrt{x}+1)} \cdot \dfrac{5 \sqrt{x}(\sqrt{x}-2)}{2 \sqrt{x}+3}=\dfrac{5 \sqrt{x}}{2 \sqrt{x}+1} \end{array}\)
Vậy với \(x>0, x \neq 4\). thì \(A=\dfrac{5 \sqrt{x}}{2 \sqrt{x}+1}\)
2) Khi \(x=3-2 \sqrt{2}=(\sqrt{2}-1)^{2} ⇒ \sqrt{x}=\sqrt{2}-1\)
thay vào ta có:
\(A=\dfrac{5(\sqrt{2}-1)}{2(\sqrt{2}-1)+1}=\dfrac{5(\sqrt{2}-1)}{2 \sqrt{2}-1}=\dfrac{5(\sqrt{2}-1)(2 \sqrt{2}+1)}{7}=\dfrac{5(3-\sqrt{2})}{7}\)
3) Ta có \(\sqrt{x}>0, \forall x>0, x \neq 4\) nên \(A=\dfrac{5 \sqrt{x}}{2 \sqrt{x}+1}>0, x>0, x \neq 4\)
\(A=\dfrac{5 \sqrt{x}}{2 \sqrt{x}+1}=\dfrac{5}{2}-\dfrac{5}{2(2 \sqrt{x}+1)}<\dfrac{5}{2}, x>0, x \neq 4 ⇒ 0<> kết hợp với A nhận giá trị là một số nguyên thì \(A \in\{1,2\}\).
\(A=1 \Leftrightarrow 5 \sqrt{x}=2 \sqrt{x}+1 ⇒ \sqrt{x}=\dfrac{1}{3} \Leftrightarrow x=\dfrac{1}{9}\) thỏa mãn điêu kiện.
\(A=2 \Leftrightarrow 5 \sqrt{x}=4 \sqrt{x}+2 \Leftrightarrow \sqrt{x}=2 \Leftrightarrow x=4\) không thỏa mãn điêu kiện.
Vậy với \(x=\dfrac{1}{9}\) thì A nhận giá trị là nguyên.
Câu 2
a) Xét \(a \cdot c=-m^{2}+m-2=-\left(m-\dfrac{1}{2}\right)^{2}-\dfrac{3}{4}<0, \forall m \in \mathbb{R}\)
Vậy phương trình luôn có hai nghiệm trái dấu với mọi m.
b) Gọi hai nghiệm của phưong trình đã cho là \(x_{1}, x_{2}\).
Theo câu a) thì \(x_{1} x_{2} \neq 0\) , do đó A được xác định với mọi \(x_{1}, x_{2}\). Do \(x_{1}, x_{2}\) trái dấu nên \(\left(\dfrac{x_{1}}{x_{2}}\right)^{3}=-t\) với \(t>0\), suy ra \(\left(\dfrac{x_{2}}{x_{1}}\right)^{3}<0\), suy ra \(A < 0\)
Đặt \(\left(\dfrac{x_{1}}{x_{2}}\right)^{3}=-t,\) với t>0, suy ra \(\left(\dfrac{x_{2}}{x_{1}}\right)^{3}=-\dfrac{1}{t} .\)
Khi đó \(A=-t-\dfrac{1}{t}\) mang giá trị âm và A đạt giá trị lớn nhất khi -A có giá trị nhỏ nhất.
Ta có \(-A=t+\dfrac{1}{t} \geq 2\), suy ra \(A \leq-2\). Đẳng thức xảy ra khi và chi khi \(t=\dfrac{1}{t} \Leftrightarrow t^{2}=1 ⇒ t=1\). Với t = 1, ta có
\(\left(\dfrac{x_{1}}{x_{2}}\right)^{3}=-1 \Leftrightarrow \dfrac{x_{1}}{x_{2}}=-1 \Leftrightarrow x_{1}=-x_{2} \Leftrightarrow x_{1}+x_{2}=0 \Leftrightarrow-(m-1)=0 \Leftrightarrow m=1 \)
Vậy với m=1 thì biểu thức A đat giá trị lớn nhất là -2 .
Câu 3.
Gọi vận tốc riêng của ca nô là x (km/h, x>0)
Và vận tốc cùa dòng nưóc là y (km /h, y>0)
Ca nô xuôi dòng đi với vận tốc x+y (km /h). Đi đoạn đường 78 km nên thời gian đi là \(\dfrac{78}{x+y}\) (giờ).
Ca nô đi ngược dòng với vận tốc x-y (km /h) . Đi đoạn đường 44 km nên thời gian đi là \(\dfrac{44}{x-y}\) (giờ).
Tổng thời gian xuôi dòng là 78 km và nguọc dòng là 44 km mất 5 giờ nên ta có phương trình:
\(\dfrac{78}{x+y}+\dfrac{44}{x-y}=5 (1)\)
Ca nô xuôi dòng 13 km và ngược dòng 11 km nên ta có phương trình:
\(\dfrac{13}{x+y}+\dfrac{11}{x-y}=1\) (2). Tù (1) và (2) ta có hệ phưong trình:
\(\left\{\begin{array}{l}\dfrac{78}{x+y}+\dfrac{44}{x-y}=5 \\ \dfrac{13}{x+y}+\dfrac{11}{x-y}=1\end{array} \Leftrightarrow\left\{\begin{array}{l}x+y=26 \\ x-y=22\end{array} \Leftrightarrow\left\{\begin{array}{l}x=24 \\ y=2\end{array} .\right.\right.\right.\)
Đối chiếu với điều kiện ta thấy thỏa mãn.
Vậy vận tốc riêng của ca nô là 24 km/h và vận tốc của dòng nước là 2 km/h.
Câu 4.
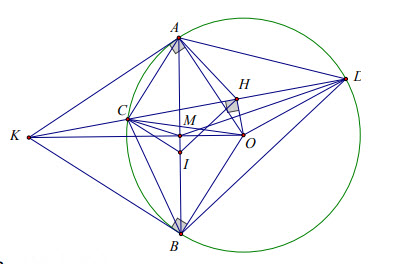
a) Vì KA, KB là các tiếp tuyến của (O) nên ∠KAO = ∠KBO = 90⁰.
Do H là trung điểm của dây CD nên ∠KHO = 90⁰
Từ đó suy ra 5 điểm K, A, H, O, B cùng nằm trên đường tròn đường kính KO.
b) Vi M là trung điểm của AB nên AM ⊥ KO. Áp dụng hệ thức lượng trong tam giác vuông KAO => KM.KO = KA².
Xét tam giác KAC và tam giác KDA có
∠KAC = ∠KDA (Tính chất góc tạo bởi tiếp tuyến và dây cung).
Góc AKD chung .
Nên △KAC ∽ △KDA(g.g) .
=> \(\dfrac{K A}{K C}=\dfrac{K D}{K A} ⇒ KA^{2}=K C . K D .\) Suy ra \(K C . K D=K H . K O\)
⇒ \(\Delta K M C ∽ \Delta K D O(g . g) ⇒ C M K=C D O\) ⇒ CMOD nội tiếp.
c) Ta có HI // BD => ∠CHI = ∠CDB.
Mặt khác ∠CAB= ∠CDB cùng chắn cung CB nên suy ra ∠CHI = ∠CAB hay AHIC là tứ giác nội tiếp. Do đó ∠IAH = ∠ICH ⇔ ∠BAH = ∠ICH.
Mặt khác ta có A, K, B, O, H cùng nằm trên đường tròn đường kính OK nên ∠BAH = ∠BKH. Từ đó suy ra
∠ICH = ∠BKH ⇒ CI // KB .
Mà KB ⊥ OB ⇒ C I ⊥ OB
Câu 5.
Áp dụng bất đẳng thức Cauchy - Schwarz ta có:
\(x+y+z-x y z=x(1-y z)+(y+z) . 1 \leq \sqrt{\left[x^{2}+(y+z)^{2}\right]\left[(1-y z)^{2}+1\right]}\)
Tới đây ta cần chứng minh
\((2+2 y z)\left(2-2 y z+y^{2} z^{2}\right) \leq 4 \Leftrightarrow y^{3} z^{3}-y^{2} z^{2} \leq 0 \Leftrightarrow y^{2} z^{2}(y z-1) \leq 0 .\)
Mặt khác theo giả thiết ta có \(2=x^{2}+y^{2}+z^{2} \geq y^{2}+z^{2} \geq 2 y z ⇒ y z \leq 1.\)
Nên bất đẳng thức trên luôn đúng. Dấu bằng xảy ra khi và chỉ khi có 2 số bằng 1 và một số bằng 0 .
Trên đây là lời giải chi tiết đề thi thử vào 10 môn toán năm 2021 lần 1 của tỉnh Bắc Kạn, mong rằng đây sẽ là tài liệu hữu ích giúp các em ôn tập. Đừng quên còn rất nhiều tài liêu đề thi thử vào lớp 10 môn toán khác của các tỉnh thành trên cả nước nhé.
