Đề thi thử vào 10 là một trong những cách thức giúp các em ôn tập và làm quen mẫu đề thi trước khi tiến vào kì thi chính thức. Cùng tham khảo mẫu đề thi thử vào 10 môn Toán 2020 trường THCS Liên Chung dưới đây nhé:
Đề thi
PHẦN 1: Trắc nghiệm khách quan (2 điểm)
Hãy viết vào bài thi chỉ một chữ cái A (hoặc B, C, D) đứng trước câu trả lời đúng vào bài thi:
Câu 1: Biểu thức \(\sqrt{(1-\sqrt{2})^2}\) có giá trị là:
A. 1 - √2
B. 1 + √2
C. √2 - 1
D. 1
Câu 2: Hàm số \(y = (3 - 5m)x +3\)và hàm số \(y = (m - 2)x - 1\) có đồ thị là hai đường thẳng song song với nhau khi:
A. m = \(\dfrac{5}{6}\)
B. m = \(\dfrac{6}{5}\)
C. m = \(- \dfrac{4}{5}\)
D. m = \(\dfrac{5}{4}\)
Câu 3: Điều kiện xác định của \(\sqrt{2-3x}\) là:
A. \(x ≥ \dfrac{2}{3}\)
B. \(x >\dfrac{2}{3}\)
C. \( x ≤ - \dfrac{2}{3}\)
D. \(x ≤ \dfrac{2}{3}\)
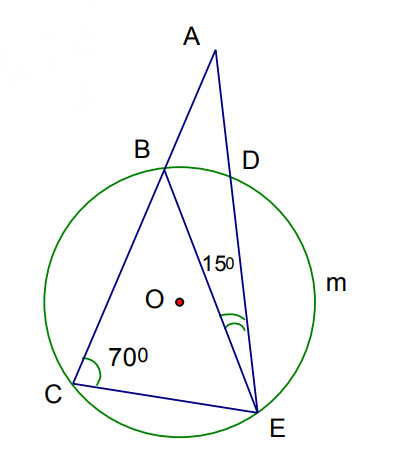
Câu 4: Cho hình vẽ. Số đo cung DmE bằng:
A. 100 ⁰
B. 110⁰
C. 90⁰
D. 55⁰.
PHẦN 2: TỰ LUẬN (8 điểm)
Câu 5: Giải phương trình và hệ phương trình sau:
a. \(x^4 - 5x^2 + 6 = 0\)
b. \(\left\{ \matrix{ x - 2y = 5 \hfill \cr 2x - y = 16 \hfill \cr} \right.\)
Câu 6: Cho phương trình \(x^2 - 2(m-3)x - 2m + 5 = 0 \)
(1) (ẩn x, m là tham số)a. Giải phương trình với m = 3
b. Tìm m để phương trình có hai nghiệm phân biệt
c. Gọi \(x₁, x₂\) là hai nghiệm của phương trình (1). Tìm m để P = \(x₁^2 + x₂^2\) đạt giá trị nhỏ nhất.
Câu 7: Hai người cùng làm chung một công việc thì sau 5 giờ sẽ xong. Nếu họ cùng làm trong 4 giờ sau đó người một nghỉ, người hai làm tiếp phần việc còn lại trong 6 giờ nữa mới xong. Hỏi nếu làm riêng thì mỗi người hoàn thành công việc trong bao lâu.
Câu 8: Cho tứ giác ABCD nội tiếp đường tròn (O) đường kính BD (\(∠ADC > 90⁰\) ). Các đường thẳng AB, CD cắt nhau tại E; các đường thẳng AD và BC cắt nhau tại F.
a. Chứng minh rằng: BD ⊥ EF (gọi H là chân đường vuông góc)
b. Chứng minh rằng D là tâm đường tròn nội tiếp tam giác AHC
c. Cho ∠ADC = 135⁰ , BD = 10cm. Tính AC
Câu 9: Cho a, b, c > 0 . Chứng minh rằng:
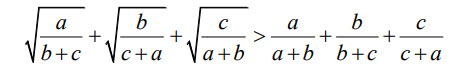
Hết
Đáp án đề thi thử vào 10 THCS Liên Chung
PHẦN 1: Trắc nghiệm khách quan (2 điểm)
Câu 1: C
Câu 2: A
Câu 3: D
Câu 4: D
PHẦN 2: Tự luận (8 điểm)
Câu 5: Giải phương trình và hệ phương trình sau:
a. \(x^4 - 5x^2 + 6 = 0\)
\(\Leftrightarrow (x^2-3)(x^2-2)=0\)
\(\Leftrightarrow \left\{ \matrix{ x^2 = 3 \hfill \cr x^2 = 2\hfill \cr} \right.\)
\(\Leftrightarrow\left\{ \matrix{ x=±\sqrt{3} \hfill \cr x=±\sqrt{2} \hfill \cr} \right.\)
Kết luận: Phương trình có 4 nghiệm \((-\sqrt{2};\sqrt{2};-\sqrt{3};\sqrt{3})\)
b. \(\left\{ \matrix{ x - 2y = 5 \hfill \cr 2x - y = 16 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ x = 5 + 2y \hfill \cr 2x - y =16 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ x = 5 + 2y \hfill \cr 2(5+2y) - y =16 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ x = 5 + 2y \hfill \cr 3y+10 =16 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ x = 5 + 2y \hfill \cr 3y+10 =16 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ x = 5 + 2y \hfill \cr y=2 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ x =9 \hfill \cr y=2 \hfill \cr} \right.\)
Kết luận: Phương trình có 1 cặp nghiệm \((x;y)=(9;2)\)
Câu 6: Cho phương trình \(x^2 - 2(m-3)x - 2m + 5 = 0 \) (1) (ẩn x, m là tham số)
a. Giải phương trình với m = 3
Với m = 3, thay vào phương trình (1) ta có:
\(x^2 - 2(3-3)x - 2.3+5 = 0\)
\(\Leftrightarrow x^2 - 1 = 0\)
\(\Leftrightarrow x^2 = 1 \Leftrightarrow x = ±1 \)
Kết luận: Phương trình có 2 nghiệm \(x=±1\)
b. Tìm m để phương trình có hai nghiệm phân biệt
Để phương trình có 02 nghiệm phân biệt \(\Leftrightarrow △'>0\)
Ta có: \(△'=[-(m-3)]^2 - (2m-5) ×1 = (m^2-6m+9) - 2m +5 = m^2 - 8m + 14\)
Để \(△'>0 \Leftrightarrow m^2 - 8m + 14>0 \)
\(\Leftrightarrow \left[ \matrix{ {m} > 4+\sqrt{2} \hfill \cr {m} > 4-\sqrt{2} \hfill \cr} \right.\)
Kết luận: Để phương trình có 02 nghiệm phân biệt \(\Leftrightarrow \left[ \matrix{ {m} > 4+\sqrt{2} \hfill \cr {m} > 4-\sqrt{2} \hfill \cr} \right.\)
c. Gọi \(x₁, x₂\) là hai nghiệm của phương trình (1). Tìm m để P = \(x₁^2 + x₂^2\) đạt giá trị nhỏ nhất.
Vì \(x₁, x₂\) là 2 nghiệm của phương trình (1), nên theo định lý Vi-et, ta có:
\(\left\{ \matrix{ x_1+x_2=2(m-3)\hfill \cr x_1.x_2 = -2m+5 \hfill \cr} \right.\) (2)
Ta có:
\(P = x_1^2 + x_2^2 = (x_1+x_2)^2 - 2x_1x_2\)
Thay (2) vào P ta có:
\(\Leftrightarrow P = [2(m-3)]^2-2(-2m+5)\)
\(\Leftrightarrow P = 4m^2-24m+36+4m-10 = 4m^2 - 20m+26 = (2m-5)^2 + 1 \)
Ta thấy \((2m-5)^2 ≥ 0 \Leftrightarrow P ≥ 1\)
Vậy P đạt giá trị nhỏ nhất \(P=1 \Leftrightarrow 2m-5=0 \Leftrightarrow m=\cfrac{5}{2}\)
Câu 7: Hai người cùng làm chung một công việc thì sau 5 giờ sẽ xong. Nếu họ cùng làm trong 4 giờ sau đó người một nghỉ, người hai làm tiếp phần việc còn lại trong 6 giờ nữa mới xong. Hỏi nếu làm riêng thì mỗi người hoàn thành công việc trong bao lâu.
Giải
Gọi công suất người 1 và người 2 làm việc mỗi giờ lần lượt là A và B.
X là công việc họ cần hoàn thành.
Theo bài ra ta có:
\(\left\{ \matrix{ 5A+5B = X \hfill \cr 4A+4B+6B = X \hfill \cr} \right. \)
\( \Leftrightarrow \left\{ \matrix{ 5A+5B=X \hfill \cr A=5B \hfill \cr} \right.\)
\( \Leftrightarrow \left\{ \matrix{ 6A=X \hfill \cr 30B=X \hfill \cr} \right.\)
Vậy nếu người 1 làm việc độc lập thì hết 6 giờ, người 2 làm việc độc lập thì hết 30 giờ
Câu 8: Cho tứ giác ABCD nội tiếp đường tròn (O) đường kính BD (\(∠ADC > 90⁰\) ). Các đường thẳng AB, CD cắt nhau tại E; các đường thẳng AD và BC cắt nhau tại F.
a. Chứng minh rằng: BD ⊥ EF (gọi H là chân đường vuông góc)
b. Chứng minh rằng D là tâm đường tròn nội tiếp tam giác AHC
c. Cho ∠ADC = 135⁰ , BD = 10cm. Tính AC.
Giải
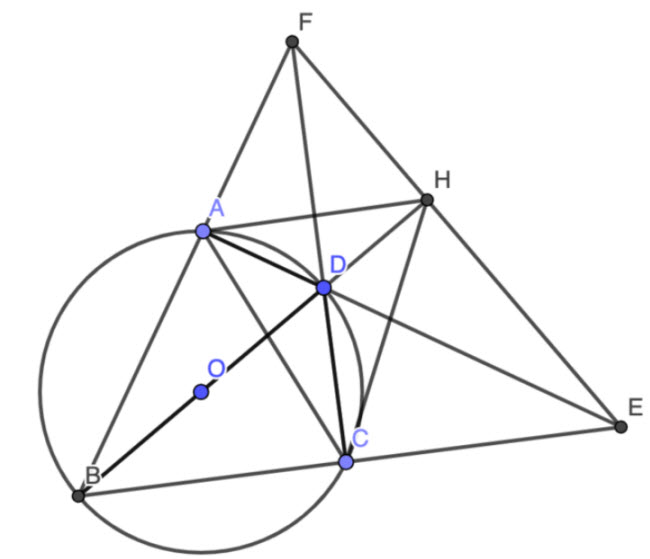
a. Ta có tứ giác ABCD nội tiếp đường tròn đường kính BD nên \(\angle BAD = \angle BCD = 90⁰\)
\(\Leftrightarrow \left\{\matrix{DC \bot BC \hfill\cr DA \bot AB \hfill\cr}\right.\)\(\Rightarrow \triangle BEF \) có FC và EA là đường cao, lại có \(FC \cap EA = {D} \) \(\Rightarrow \triangle BEF \) có D là trực tâm (giao của 3 đường cao) \(\Rightarrow BD \bot EF\) (đpcm)
b. Theo phần a, ta có D là trực tâm tam giác BEF \(\angle DHE = \angle DCE = 90⁰ \Leftrightarrow \) tứ giác CDHE nội tiếp \(\Rightarrow \angle HDE = \angle HCE\) (góc nội tiếp cùng chắn cung HE)
Để chứng minh D là tâm đường tròn nội tiếp tam giác AHC, ta đi chứng minh D là giao của 3 đường phân giác trong của tam giác AHC.
Thật vậy \(\angle DCA =\angle DCB - \angle ACB = 90⁰-\angle ACB = 90⁰-\angle ADB \)(góc nội tiếp đường tròn (O) cùng chắn cung AB) \( = 90⁰-\angle HDE \) (2 góc đối đỉnh) \( = 90⁰-\angle HDE =90⁰-\angle HCE \)(vừa chứng minh) \( = \angle DCH\).
Vậy ta có \(\angle DCA = \angle DCH\) hay CD là tia phân giác trong của góc ACH.
Chứng minh tương tự ta được \(\angle DAC = \angle DAH\)hay AD là tia phân giác trong của góc CAH.
Từ đó suy ra D là giao của 3 đường phân giác trong của tam giác ACH hay D là tâm đường tròn nội tiếp tam giác ACH (đpcm).
c. Ta đặt \(\angle ADB = \alpha \)
Xét tam giác ABD vuông tại A, ta có \(AD = BD.cos \angle ADB=10cos {\alpha}\) tương tự với tam giác ACD, ta cũng có \(CD = BD.cos \angle CDB=10.cos(\angle ADC - \angle ADB)=10.cos({3\pi\over 4}-\alpha)\)
\(=10.cos({\pi\over 2}+{\pi\over 4}-\alpha)=10.sin(\alpha-{\pi\over 4})=10.{{sin\alpha-cos\alpha}\over{\sqrt{2}}}=5\sqrt{2}(sin\alpha-cos\alpha)\)
Áp dụng định lý Cos cho tam giác ADC, ta có:
\(AC^2 = AD^2 + DC^2 - 2.AD.DC.cos \angle ADC \)
Thay vào ta có:
\(AC^2 = (10cos {\alpha})^2+ [5\sqrt{2}(sin\alpha-cos\alpha)]^2 - 2.10cos {\alpha}.[5\sqrt{2}(sin\alpha-cos\alpha)].cos {3\pi\over{4}}\)
\(AC^2 = 100cos^2 {\alpha}+50(sin^2\alpha+cos^2\alpha-2sin\alpha.cos\alpha) + 100.cos {\alpha}.(sin\alpha-cos\alpha)\)
\(AC^2 = 100cos^2 {\alpha}+50(1-2sin\alpha.cos\alpha) + 100.cos {\alpha}.sin\alpha-100.cos^2 {\alpha} = 50\)
\(\Rightarrow AC = 5\sqrt{2}\).
Câu 9: Cho a, b, c > 0 . Chứng minh rằng:
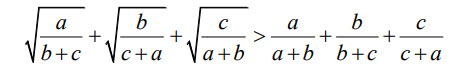
Giải
Đặt \(Q = {\sqrt{a\over{b+c}}}+ {\sqrt{b\over{c+a}}}+ {\sqrt{c\over{a+b}}}\)
\(P = {a\over{a+b}}+ {b\over{b+c}}+{c\over{c+a}}\)
Ta đi chứng minh: \( {a\over{a+b}} < {a+c\over{a+b+c}}\) với \(a,b,c>0\), thật vậy:
\( {a\over{a+b}} < {a+c\over{a+b+c}} \Leftrightarrow a(a+b+c) < (a+b)(a+c)\) (vì \(a,b,c>0\))
\(\Leftrightarrow a^2+ab+ac <>
\(\Leftrightarrow 0 <> luôn đúng với \(a,b,c>0\)
\(\Leftrightarrow {a\over{a+b}} < {a+c\over{a+b+c}}\)(đpcm)
Tương tự ta chứng minh được \({b\over{b+c}} < {b+a\over{a+b+c}}\) và \( {c\over{c+a}} < {c+b\over{a+b+c}}\)
\(⇒ P = {a\over{a+b}}+ {b\over{b+c}}+{c\over{c+a}} < {a+c\over{a+b+c}}+{b+a\over{a+b+c}}+{c+b\over{a+b+c}} ={2(a+b+c)\over{a+b+c}}=2\)
\(⇒ P <2\) (1)
Áp dụng bất đẳng thức Cauchy cho 2 số dương \({{b+a}\over{c}} \) và 1 ta có:
\({{b+a}\over{c}} +1 ≥2{\sqrt{b+a\over{c}}}\)
\(\Leftrightarrow {{a+b+c}\over{c}} ≥2{\sqrt{b+a\over{c}}}\)
\(\Leftrightarrow {{2c}\over{a+b+c}} ≤{\sqrt{c\over{b+a}}}\)
Tương tự ta chứng minh được \( {{2a}\over{a+b+c}} ≤{\sqrt{a\over{b+c}}}\) và \( {{2b}\over{a+b+c}} ≤{\sqrt{b\over{a+c}}}\), từ 3 điều trên ta có:
\(Q = {\sqrt{a\over{b+c}}}+ {\sqrt{b\over{c+a}}}+ {\sqrt{c\over{a+b}}} ≥ {{2a}\over{a+b+c}}+{{2b}\over{a+b+c}}+{{2c}\over{a+b+c}}= {{2(a+b+c)}\over{a+b+c}}=2\)
\(\Leftrightarrow Q ≥ 2\) mà ta dễ thấy dấu = không xảy ra \(⇒ Q > 2\) (2).
Từ (1) và (2) ta có \(Q>2>P ⇒ Q>P \) hay ta có điều phải chứng minh
Trên đây là mẫu đề thi thử vào lớp 10 môn Toán có đáp án chi tiết của trường THCS Liên Chung ra đề, cùng bỏ giấy ra và thực hiện đề thi này trong vòng 120 phút em nhé!
