Đọc tài liệu đã sưu tầm được rất nhiều bộ đề thi thử vào 10 môn Toán của các trường trên cả nước với mong muốn giúp các em ôn thi được tốt nhất. Dưới đây là đề thi thử vào lớp 10 môn Toán năm 2020 để các em thử sức
Đề thi thử
Bài I (2,0 điểm)
Cho các biểu thức \(A = \dfrac{2\sqrt x}{\sqrt x +3} \) và \(B = \dfrac{\sqrt x+1}{\sqrt x -3} + \dfrac{11\sqrt x-3}{x-9} \); với \(x\geq 0; x ≠ 9 \).
1. Tính giá trị của biểu thức A khi x = 36.
2. Rút gọn biểu thức M = A + B.
3. Tìm x sao cho M = M⁴.
Bài II (2,5 điểm)
1. Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Quãng đường AB dài 48km, trong đó đoạn đường qua khu dân cư dài 8km. Một ô tô đi từ A đến B với vận tốc quy định. Khi đi qua khu dân cư, xe phải giảm vận tốc 10km/h so với vận tốc quy định. Tính vận tốc của ô tô khi đi qua khu dân cư, biết rằng thời gian đi từ A đến B là 1 giờ.
2. Tính thể tích hình cầu nếu diện tích của mặt cầu là \(16 \pi \space {cm}^2\).
Bài III (2,0 điểm)
1. Cho đường thẳng (d): y = mx - m + 1 và parabol (P): \(y = x^2\).
a. Tìm giá trị của m để đường thẳng (d) và parabol (P) cắt nhau tại hai điểm phân biệt.
b. Gọi \(x_1; x_2\) là hoành độ các giao điểm của (d) và (P). Tìm m sao cho:
\(x_1^2x_2 + x_2^2x_1 = 2\)
2. Giải hệ phương trình
\(\left\{ \matrix{ x+ \sqrt y =5 \hfill \cr 2x - \sqrt y = 4 \hfill \cr} \right.\)
Bài IV (3,0 điểm)
Cho đường tròn (O;R) với dây BC cố định (BC không đi qua O). Gọi A là điểm chính giữa cung nhỏ BC và điểm E thay đổi trên cung lớn BC. Nối AE cắt BC tại D. Gọi I là trung điểm BC. Kẻ CH vuông góc với AE tại H, nối EB cắt CH tại M.
1. Chứng minh AD.AE = AB².
2. Chứng minh 4 điểm A, I, C, H cùng thuộc một đường tròn.
3. So sánh AM và AC. Tìm vị trí của E để diện tích tam giác AMC lớn nhất.
Bài V (0,5 điểm)
Tìm x, y > 0 sao cho:
\(\left(x^2+y+ \dfrac{3}4 \right) \left(y^2+x+ \dfrac{3}4 \right) = \left(2x+ \dfrac{1}2 \right) \left(2y+ \dfrac{1}2 \right)\)
---Hết---
Xem thêm các tài liệu đề thi thử toán vào lớp 10 tại Hà Nội năm 2020 nữa em nhé!
Đáp án
Bài I:
1.
Thay x = 36 vào A ta có:
\(A = \dfrac{2\sqrt x}{\sqrt x +3} = \dfrac{2\sqrt {36}}{\sqrt {36} +3} = \dfrac{4}{3} \)
2.
Với \(x\geq 0; x ≠ 9 \), ta có:
\(M = A + B = \dfrac{2\sqrt x}{\sqrt x +3} + \dfrac{\sqrt x+1}{\sqrt x -3} + \dfrac{11\sqrt x-3}{x-9} \)
\(= \dfrac{2\sqrt x (\sqrt x-3) + (\sqrt x+1)(\sqrt x+3)+11\sqrt x-3}{(\sqrt x +3)(\sqrt x -3)} \)
\(= \dfrac{3x+9\sqrt x}{(\sqrt x +3)(\sqrt x -3)} \)
\(= \dfrac{3\sqrt x}{\sqrt x -3} \)
3.
Để \(M = M^4\)
\(\Leftrightarrow \left[ \matrix{ M = 0 \hfill \cr M = 1\hfill \cr} \right.\)
\(\Leftrightarrow \left[ \matrix{ \dfrac{3\sqrt x}{\sqrt x -3} = 0 \hfill \cr \dfrac{3\sqrt x}{\sqrt x -3} = 1\hfill \cr} \right.\)
\(\Leftrightarrow \left[ \matrix{ x = 0 \space (tm \space đkxđ)\hfill \cr {3\sqrt x} = {\sqrt x -3} \Rightarrow {2\sqrt x} =-3 \space (loại) \hfill \cr} \right.\)
KL......
Bài II:
1.
Gọi vận tốc của ô tô khi đi qua khu dân cư là X (km/h; X > 0)
Vận tốc trên quãng đường thường là X + 10 (km/h)
Theo bài ra ta có:
\(\dfrac{48-8}{X+10} + \dfrac{8}{X} = 1\)
\(\Leftrightarrow X^2 -38X - 80 = 0\)
\(\Leftrightarrow \left[ \matrix{ X = 40 \hfill \cr X = -2 \hfill \cr} \right.\)
Vì X > 0 ⇒ X = 40 (km/h).
2.
Diện tích mặt cầu là:
\(S = 4\pi r^2 = 16 \pi \) \(\Rightarrow r = 2 \space (cm)\)
\(\Rightarrow V = \dfrac{4}3\pi r^3 = \dfrac{32}3\pi \space ({cm}^3)\).
Bài III:
1. Cho đường thẳng (d): y = mx - m + 1 và parabol (P): \(y = x^2\).
a.
Xét phương trình hoành độ giao điểm của (d) và (P) ta có:
\( x^2 = mx - m + 1\)
\(\Leftrightarrow x^2 - mx + m - 1 = 0\) (1)
Để (d) và (P) cắt nhau tại 2 điểm phân biệt ⇔
\(\Delta = m^2 - 4m + 4 = (m-2)^2 >0\) ⇔ m ≠ 2.
b.
Ta thấy \(\Delta \geq 0\) với mọi m nên (d) luôn cắt (P).
Áp dụng hệ thức Vi-ét cho (1), ta có:
\(\left\{ \matrix{ x_1+x_2 = m \hfill \cr x_1x_2 = m + 1\hfill \cr} \right.\)
Ta có:
\(x_1^2x_2 + x_2^2x_1 = 2\)
\(\Leftrightarrow x_1x_2(x_1+x_2) = 2\)
\(\Leftrightarrow (m+1)m= 2\)
\(\Leftrightarrow \left[ \matrix{ m = 1 \hfill \cr m = -2 \hfill \cr} \right.\) (thoả mãn...)
KL....
2.
\(\left\{ \matrix{ x+ \sqrt y =5 \hfill \cr 2x - \sqrt y = 4 \hfill \cr} \right.\)
(đkxđ \(y \geq 0\))
\(\Leftrightarrow \left\{ \matrix{ x=3 \hfill \cr \sqrt y = 2 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ x=3 \hfill \cr y= 4 \hfill \cr} \right.\)
Bài IV:
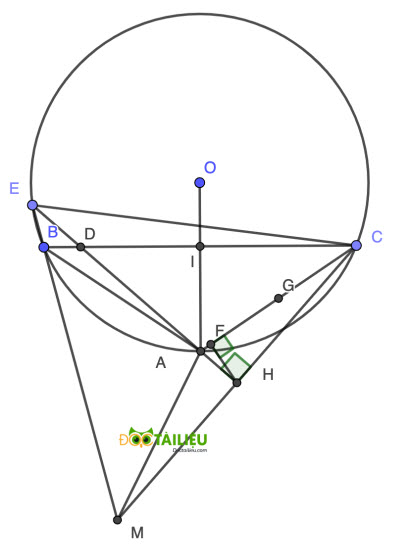
1.
Vì A là điểm chính giữa cung BC ⇒ \( \stackrel\frown{AB} = \stackrel\frown{AC}\) ⇒ ∠ABC = ∠AEB (góc nội tiếp chắn 2 cung bằng nhau) hay ∠ABD = ∠AEB.
Xét △ABE và △ADB có:
Góc BAD chung
∠ABD = ∠AEB (cmt)
Suy ra △ABE ∽ △ADB ⇒ \(\dfrac{AB}{AE} = \dfrac{AD}{AB} \) ⇒ AD.AE = AB² (đpcm).
2.
Vì A là điểm chính giữa cung BC ⇒ OA ⊥ BC và OA đi qua trung điểm của BC, hay O, I, A thẳng hàng ⇒ ∠OIC = 90°.
Theo giả thiết ta cũng có ∠AHC = 90° = ∠AIC ⇒ I và H cùng thuộc đường tròn đường kính AC, hay 4 điểm A, I, C, H cùng thuộc một đường tròn (đpcm).
3.
Vì A là điểm chính giữa cung BC ⇒ EA là phân giác của góc BEC.
Xét △EMC có EH vừa là phân giác góc BEC, vừa là đường cao ⇒ △EMC cân tại E ⇒ H là trung điểm của MC.
Xét △AMC có AH là đường cao, H là trung điểm MC ⇒ △AMC cân tại A ⇒ AM = AC.
Từ H kẻ HF vuông góc với AC tại F.
Lấy G là trung điểm của AC.
Xét △AHC vuông tại H có G là trung điểm AC ⇒ \(HG = GA = GC = \dfrac{1}2 AC\).
Lại có \(HF \leq HG = \dfrac{1}2 AC\) (theo tính chất đường cạnh huyền)
Vì H là trung điểm MC (cmt) ⇒ MC = 2 HC
⇒ \(S_{\triangle AMC} = 2 S_{\triangle AHC} = AC. HF \leq \dfrac{1}2{AC}^2 \).
Vậy \({Max}_{S_{\triangle AMC}} = \dfrac{1}2{AC}^2 \) ⇔ HG ⊥ AC ⇔ △AHC cân tại H.
Mà △AHC vuông tại H ⇒ ∠EAC = ∠DAC = 45°.
Suy ra để diện tích tam giác AMC lớn nhất thì điểm E phải thuộc cung lớn BC thoả mãn ∠EAC = 45°.
Bài V:
Áp dụng BĐT AM-GM cho \(x^2\) và \(\dfrac{1}4\) ta có:
\(x^2 + \dfrac{1}4 \geq 2\sqrt{\dfrac{x^2}4} = x\)
\(\Leftrightarrow x^2 + y + \dfrac{3}4 \geq x + y + \dfrac{1}2\)
Tương tự, ta có:
\(\left(x^2+y+ \dfrac{3}4 \right) \left(y^2+x+ \dfrac{3}4 \right) \geq \left( x+y + \dfrac{1}2\right)^2\) (1)
Ta đi chứng minh:
\( \left( x+y + \dfrac{1}2\right)^2 \geq \left(2x+ \dfrac{1}2 \right) \left(2y+ \dfrac{1}2 \right)\)
\(\Leftrightarrow (x+y)^2 + (x+y) + \dfrac{1}4 \geq 4xy +(x+y) + \dfrac{1}4\)
\(\Leftrightarrow (x+y)^2 \geq 4xy \)
\(\Leftrightarrow (x-y)^2 \geq 0\) Luôn đúng với mọi x, y; mà các phép biến đổi là tương đương nên ta có
\( \left( x+y + \dfrac{1}2\right)^2 \geq \left(2x+ \dfrac{1}2 \right) \left(2y+ \dfrac{1}2 \right)\) (2)
Từ (1) và (2) suy ra:
\(\left(x^2+y+ \dfrac{3}4 \right) \left(y^2+x+ \dfrac{3}4 \right) \geq \left(2x+ \dfrac{1}2 \right) \left(2y+ \dfrac{1}2 \right)\) (*)
Để phương trình đã cho có nghiệm khi và chỉ khi dấu bằng của (*) xảy ra, hay \( x = y = \dfrac{1}2\).
KL.....
-/-
Đọc tài liệu vừa chia sẻ đến các em đề thi thử Tón vào lớp 10 của trường THCS Trần Phú (Phú Xuyên - Hà Nội), còn rất nhiều bộ đề thi thử Toán vào lớp 10 của các trường khác trên cả nước đã được chúng tôi biên tập, thường xuyên truy cập vào trang để cập nhật nhé
