Đọc tài liệu đã sưu tầm được rất nhiều bộ đề thi thử vào 10 môn Toán của các trường trên cả nước với mong muốn giúp các em ôn thi được tốt nhất. Dưới đây là đề thi thử vào lớp 10 môn Toán năm 2020 để các em thử sức
Đề thi thử
|
PHÒNG GD&ĐT CHƯƠNG MỸ - ĐỀ CHÍNH THỨC - |
ĐỀ KIỂM TRA KHẢO SÁT CHẤT LƯỢNG MÔN: Toán 9 Năm học 2019-2020 Thời gian làm bài 120 phút (Không kể thời gian phát đề) |
Bài I. (2 điểm)
Cho biểu thức \(A = \dfrac{3-\sqrt{x}}{\sqrt{x}-2}+1\)
và \(B = \dfrac{\sqrt{x}}{\sqrt{x}-2} - \dfrac{\sqrt{x}+1}{\sqrt{x}+2}+\dfrac{2\sqrt{x}+7}{4-x}\)
với x ≥ 0; x ≠ 4
1) Tính giá trị của biểu thức A khi x = 16;
2) Rút gọn biểu thức P = B : A;
3) Tìm số nguyên tố x lớn nhất để |P| > P.
Bài II. (2,5 điểm)
1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Một đội xe dự định dùng một số lượng xe cùng loại để chở hết 360 tấn hàng. Lúc sắp khởi hành, có 3 xe phải điều đi làm việc khác. Vì vậy, mỗi xe phải chở thêm 4 tấn hàng nữa mới hết số hàng đó. Tính số lượng xe thực tế tham gia chở hàng của đội, biết rằng khối lượng hàng mỗi xe phải chở là bằng nhau.
2) Nón làng Chuông là một hình nón có đường kính đáy bằng 40 cm, độ dài đường sinh là 30 cm. Người ta lát mặt xung quanh hình nón bằng 3 lớp lá khô. Tính diện tích lá cần dùng để làm nên một chiếc nón như vậy.
Bài III (2,0 điểm)
1) Giải phương trình: \((x^2-2)^2 + 5(x^2-2) – 6 = 0\)
2) Cho parabol (P): y = x² và đường thẳng (d): y = 2(m - 1)x -2m + 5 (m là tham số).
a) Chứng minh (d) luôn cắt (P) tại hai điểm phân biệt với mọi giá trị của m.
b) Gọi x₁, x₂ là hoành độ giao điểm của (d) và (P). Tìm các giá trị của m để √x₁ = √x₂ + 2.
Bài IV (3,0 điểm)
Cho △ABC có 3 góc nhọn (AC > AB) nội tiếp đường tròn tâm O. Kẻ đường cao AD (D thuộc BC) và đường kính AK của đường tròn tâm O. Gọi E, F theo thứ tự là chân đường vuông góc kẻ từ B và C tới AK.
1) Chứng minh: Tứ giác AEDB nội tiếp;
2) Chứng minh: DB.AC = AD.KC và DF//BK;
3) Cho BC cố định, A là điểm di động trên cung lớn BC sao cho tam giác ABC nhọn. Chứng minh rằng tâm của đường tròn ngoại tiếp △DEF là một điểm cố định.
Bài V (0,5 điểm)
Cho x, y, z là các số thực thỏa mãn (x-y)(x-z) = 1; y ≠ z
Chứng minh:
\(\dfrac{1}{(x-y)^2} + \dfrac{1}{(y-z)^2} + \dfrac{1}{(z-x)^2} ≥ 4\)
---Hết---
Một tài liệu thi thử toán vào 10 khác của TP. Hà Nội: Đề thi thử tuyển sinh vào lớp 10 môn Toán Hà Nội
Đáp án
Bài I:
1)
Với x = 16, ta có:
\(A = \dfrac{3-\sqrt{x}}{\sqrt{x}-2}+1 = \dfrac{3-\sqrt{16}}{\sqrt{16}-2}+1 = \dfrac{-1}{2}+1 = \dfrac{1}{2}\)
2)
Với x ≥ 0; x ≠ 4, ta có:
\(P = B : A = \left( \dfrac{\sqrt{x}}{\sqrt{x}-2} - \dfrac{\sqrt{x}+1}{\sqrt{x}+2}+\dfrac{2\sqrt{x}+7}{4-x} \right) :\left( \dfrac{3-\sqrt{x}}{\sqrt{x}-2}+1\right)\)
\(= \dfrac{\sqrt{x}(\sqrt{x}+2)-(\sqrt{x}+1)(\sqrt{x}-2)-2\sqrt{x}-7}{(\sqrt{x}-2)(\sqrt{x}+2)} : \dfrac{1}{\sqrt{x}+2}\)
\(= \dfrac{x+2\sqrt{x}-x+\sqrt{x}+2-2\sqrt{x}-7}{\sqrt{x}-2} \)
\(= \dfrac{\sqrt{x}-5}{\sqrt{x}-2} \)
3)
Để \(|P| > P \Leftrightarrow P < 0\)
\(\Leftrightarrow \dfrac{\sqrt{x}-5}{\sqrt{x}-2} < 0\) \(\Leftrightarrow 2 < \sqrt{x} < 5\)
\(\Leftrightarrow 4 < x < 25\).Số x nguyên tố lớn nhất thoả mãn \(4 < x < 25\) là x = 23.
KL....
Bài II:
1)
Gọi số lượng xe thực tế tham gia chở hàng của đội là A (xe, A ∈ ℕ*)
Theo bài ra ta có:
\(\dfrac{360}A + 4 = \dfrac{360}{A-3} \)
\(\Leftrightarrow 4A^2 -12 A -1080 = 0\)
\(\Leftrightarrow \left[ \matrix{ A = 18 \space (tm) \hfill \cr A = -15 \space (loại)\hfill \cr} \right.\)
KL.....
2)
Diện tích lá cần dùng là:
\(S = 3S_{xq} = 3. \pi rl = 3\pi l.\dfrac{d}2 = 3.30.20.\pi = 1800 \pi \space ({cm}^2)\)
Bài III:
1)
\((x^2-2)^2 + 5(x^2-2) – 6 = 0\)
\(\Leftrightarrow [(x^2 - 2) +6][(x^2 - 2) -1] = 0\)
\(\Leftrightarrow (x^2 + 4)(x^2 - 3) = 0\)
\(\Leftrightarrow x = ±\sqrt 3\) (vì \(x^2 +4 \geq 4 > 0\) với mọi x)
KL.....
2)
a)
Xét phương trình hoành độ giao điểm của (d) và (P) ta có:
\(x^2 = 2(m - 1)x -2m + 5\)
\(\Leftrightarrow x^2 - 2(m - 1)x +2m - 5 =0\) (*)
Ta có
\(\Delta ' = (m-1) ^2 - 2m + 5 = m^2 - 4m + 6 = (m-2)^2 + 2 > 0\)
với mọi mnên (d) luôn cắt (P) tại hai điểm phân biệt với mọi giá trị của m (đpcm).
b)
Ta thấy \(x_1;x_2 \geq 0\) \(\Rightarrow \left\{ \matrix{ x_1+x_2 \geq 0 \hfill \cr x_1x_2 \geq 0 \hfill \cr} \right.\)
Áp dụng hệ thức Vi-ét cho (*) ta có:
\(\left\{ \matrix{ x_1+x_2 = 2(m-1) \hfill \cr x_1x_2 = 2m - 5 \hfill \cr} \right.\) (đkxđ \(m \geq \dfrac{5}2\))
Ta có:
\(\sqrt {x_1} = \sqrt {x_2} + 2\)
\(\Leftrightarrow \sqrt {x_1} - \sqrt {x_2} = 2\)
\(\Rightarrow (\sqrt {x_1} - \sqrt {x_2})^2 = 4\)
\(\Rightarrow x_1+x_2 - 2\sqrt{x_1x_2} = 4\)
\(\Rightarrow 2(m-1) - 2\sqrt{2m-5} = 4\)
\(\Rightarrow m-3 =\sqrt{2m-5} \)
\(\Rightarrow m^2-6m + 9 =2m - 5\)
\(\Rightarrow m^2-8m + 14 =0\)
\(\Rightarrow \left[ \matrix{ m = 4 + \sqrt 2 \hfill \cr m = 4 - \sqrt 2 \hfill \cr} \right.\) (tm đkxđ)
KL....
Bài IV:
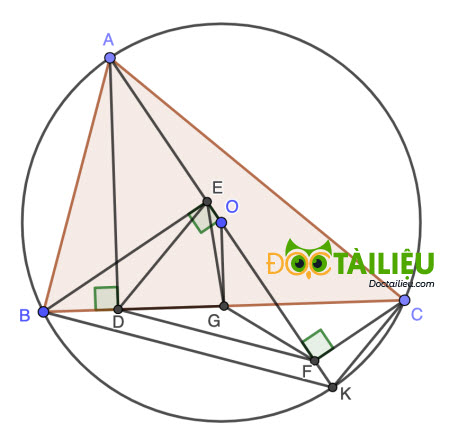
1)
Ta thấy ∠AEB = ∠ADB = 90° ⇒ E, D cùng thuộc đường tròn đường kính AB, hay tứ giác AEDB nội tiếp (đpcm).
2)
Xét △ABD và △AKC có:
∠ADB = ∠ACK = 90° (góc nội tiếp chắn đường kính AK)
∠ABD = ∠ABC = ∠AKC (góc nội tiếp cùng chắn cung AC)
Suy ra △ABD ∽ △AKC ⇒ \(\dfrac{AD}{DB} = \dfrac{AC}{KC}\) ⇒ DB.AC = AD.KC (đpcm).
Tương tự phần a, ta có ∠ADC = ∠AFC = 90° ⇒ tứ giác ADFC nội tiếp ⇒ ∠CDF = ∠CAF = ∠CAK = ∠CBK
Hay DF // BK (góc đồng vị) (đpcm).
3)
Gọi G là trung điểm của BC.
Theo tính chất dây cung ta có OG ⊥ BC hay ∠OGB = 90°.
Ta có: ∠OGB = ∠OEB = 90° ⇒ tứ giác BEOG nội tiếp ⇒ ∠OEG = ∠OBG.
Tương tự ta có ∠OGC = ∠OFC = 90° ⇒ tứ giác OGFC nội tiếp ⇒ ∠OFG = ∠OCG = ∠OBG (do △OBC cân tại O)
Suy ra ∠OEG = ∠OFG hay ∠FEG = ∠EFG ⇒ △GEF cân tại G ⇒ GE = GF (*)
Ta lại có:
∠DEG = 90° - ∠BED - ∠GEO = 90° - ∠BAD - ∠GBO = ∠ABD - ∠GBO = ∠ABO (1)
Vì tứ giác AEDB nội tiếp ⇒ ∠BAE = 180° - ∠BDE = ∠EDG (2)
Lại có △ABO cân tại O ⇒ ∠ABO = ∠BAO = ∠BAE (3)
Từ (1) (2) và (3) suy ra ∠DEG = ∠EDG ⇒ △GED cân tại G ⇒ GE = GD (**)
Từ (*) và (**) ⇒ GD = GE = GF hay G là tâm đường tròn ngoại tiếp △DEF.
Hay tâm của đường tròn ngoại tiếp △DEF là trung điểm của BC cố định (đpcm).
Bài V:
\(VT = \dfrac{1}{(x-y)^2} + \dfrac{1}{(y-z)^2} + \dfrac{1}{(z-x)^2} \)
\( = \dfrac{(z-x)^2+(x-y)^2}{(x-y)^2(z-x)^2} + \dfrac{1}{(y-z)^2}\)
\( = \dfrac{(z-x)^2+(x-y)^2}{[(x-y)(x-z)]^2} + \dfrac{1}{(y-x + x - z)^2}\)
\( = (z-x)^2+(x-y)^2 + \dfrac{1}{(y-x + x - z)^2}\)
Đặt x - y = a, x - z = b, ta có:
(x-y)(x-z) = ab = 1, và:
\(VT = b^2+a^2 + \dfrac{1}{(b-a)^2}\)
\(= (b-a)^2 + 2ab + \dfrac{1}{(b-a)^2}\)
\(= (b-a)^2 + \dfrac{1}{(b-a)^2} + 2\)
Áp dụng BĐT AM-GM cho 2 số dương ta có:
\( (b-a)^2 + \dfrac{1}{(b-a)^2} \geq 2\sqrt{(b-a)^2.\dfrac{1}{(b-a)^2}} = 2\)
\(\Leftrightarrow VT = (b-a)^2 + \dfrac{1}{(b-a)^2} + 2 \geq 4\)
Hay \(\dfrac{1}{(x-y)^2} + \dfrac{1}{(y-z)^2} + \dfrac{1}{(z-x)^2} ≥ 4\) (đpcm).
Dấu bằng xảy ra
\(\Leftrightarrow \left\{ \matrix{ ab = 1 \hfill \cr (b-a)^2 = 1 \hfill \cr} \right.\)
\(\Leftrightarrow \left[ \matrix{ a = \dfrac{1+\sqrt 5}2 \Rightarrow b = \dfrac{\sqrt 5-1}2 \hfill \cr a = \dfrac{1-\sqrt 5}2 \Rightarrow b = \dfrac{-\sqrt 5-1}2 \hfill \cr} \right.\)
và hoán vị.hay:
\(\Leftrightarrow \left[ \matrix{ (x;y;z) =\left( m;m-\dfrac{1+\sqrt 5}2;m-\dfrac{\sqrt 5-1}2 \right) \hfill \cr (x;y;z) =\left( m;m-\dfrac{1-\sqrt 5}2;m-\dfrac{-\sqrt 5-1}2 \right) \hfill \cr} \right.\) và hoán vị của y,z.
-/-
Đọc tài liệu vừa chia sẻ đến các em đề thi thử toán vào lớp 10 của Phòng GDĐT Chương Mỹ, còn rất nhiều bộ đề thi thử Toán vào lớp 10 của các trường khác trên cả nước đã được chúng tôi biên tập, thường xuyên truy cập vào trang để cập nhật nhé
