Sở GD&ĐT tình Tiền Giang vừa tổ chức kỳ thi thử tuyển sinh vào lớp 10 dành cho các em học sinh khối lớp 9 với đề thi thử môn Toán như sau:
Đề thi
Bài I. (1,5 điểm)
1. Tính giá trị biểu thức:
\(A = \sqrt{(\sqrt 5 - 2)^2} - \dfrac{5}{\sqrt 5}\)
2. Cho biểu thức:
\(P = \dfrac{3}{\sqrt x} + \dfrac{3}{\sqrt x - 3} - \dfrac{2\sqrt x - 9}{\sqrt x(\sqrt x-3)}\)
với \(x>0, x≠9\).
a) Rút gọn biểu thức P.
b) Tìm giá trị của x để P có giá trị bằng 1.
Bài II. (2,5 điểm)
1. Giải các phương trình và hệ phương trình sau:
a) \(x^2 - 4x+1=0\).
b) \(x^4 - 8x^2 - 9 = 0\)
c) \(\left\{ \matrix{ 2x + y = 6 \hfill \cr 3x - y = 4 \hfill \cr} \right.\)
2. Viết phương trình đường thẳng (d) qua A(2;5) và song song với đường thằng y = 2x + 3.
Bài III. (1,5 điểm)
Trong mặt phẳng toạ độ Oxy cho parabol (P): \(y=x^2\).
a) Vē parabol (P).
b) Bằng phép tính, tìm toạ độ điểm B thuộc (P) có hoành độ là -3.
Bài IV. (1,5 điểm)
Hai địa điểm A và B cách nhau 270km. Một người đi xe máy hướng từ địa điểm A đến địa điểm B, sau đó 1 giờ một người đi ô tô hướng từ địa điểm B đến địa điểm A và đi được 2 giờ thì gặp người đi xe máy, biết vận tốc của ô tô hơn vận tốc xe máy là 10km/h. Tính vận tốc của mỗi xe.
Bài V. (3,0 điểm)
1. Cho △ABC vuông tại A, biết AB = 6cm, BC =10cm. Tính giá trị của biểu thức
M = 3sin B + 2cos C.
2. Từ một điểm A ở ngoài đường tròn (O;R), vẽ hai tiếp tuyến AB và AC với đường tròn (B và C là hai tiếp điểm), gọi H là giao điểm của OA và BC.
a) Chứng minh AO ⊥ BC.
b) Chứng minh bốn điểm A,O,B,C cùng thuộc một đường tròn.
c) Đoạn thẳng AO cắt đường tròn (O;R) tại điểm I, vẽ IK vuông góc với AB tại K. Chứng minh IK = IH.
d) Từ điểm K vẽ tiếp tuyến thứ hai KM với đường tròn (M là tiếp điểm), KM cắt AC tại E. Biết AO = 3R, tính chu vi tam giác AKE.
Hết
Đừng quên còn rất nhiều tài liệu đề thi thử tuyển sinh vào lớp 10 tất cả các môn năm 2020 đợi các em thử sức đó!
Lời giải chi tiết
Bài I.
1.
\(A = \sqrt{(\sqrt 5 - 2)^2} - \dfrac{5}{\sqrt 5}\)
\(= (\sqrt 5 - 2) - \sqrt 5 = -2\)
2.
a)
Với \(x>0, x≠9\) ta có:
\(P = \dfrac{3}{\sqrt x} + \dfrac{3}{\sqrt x - 3} - \dfrac{2\sqrt x - 9}{\sqrt x(\sqrt x-3)}\)
\(= \dfrac{3(\sqrt x-3)+3\sqrt x-2\sqrt x + 9}{\sqrt x(\sqrt x-3)}\)
\(= \dfrac{4\sqrt x }{\sqrt x(\sqrt x-3)}\)
\(= \dfrac{4 }{\sqrt x-3}\)
b)
Để P = 1 thì:
\(P= \dfrac{4 }{\sqrt x-3} = 1\)
\(\Leftrightarrow \sqrt x-3 = 4\)
\(\Leftrightarrow x = 49\) (tm đk của x)
KL......
Bài II.
1.
a) \(x^2 - 4x+1=0\)
\(\Leftrightarrow \left[ \matrix{ x = 2 + \sqrt 3\hfill \cr x = 2 - \sqrt 3\hfill \cr} \right.\)
b) \(x^4 - 8x^2 - 9 = 0\)
\(\Leftrightarrow (x^2 -9)(x^2+1) = 0\)
\(\Leftrightarrow \left[ \matrix{ x = 3\hfill \cr x = -3\hfill \cr} \right.\) (vì \(x^2 +1 \geq 1 > 0 \))
c) \(\left\{ \matrix{ 2x + y = 6 \hfill \cr 3x - y = 4 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ x=2 \hfill \cr y=2 \hfill \cr} \right.\)
2.
Dễ thấy điểm A(2;5) không thuộc đường thẳng có phương trình y = 2x + 3.
Phương trình đường thẳng (d) có dạng:
\(y -5 = 2(x-2) \Leftrightarrow y = 2x + 1\)
Bài III.
a)
Các em nhớ kẻ bảng tọa độ điểm rồi vẽ hình.
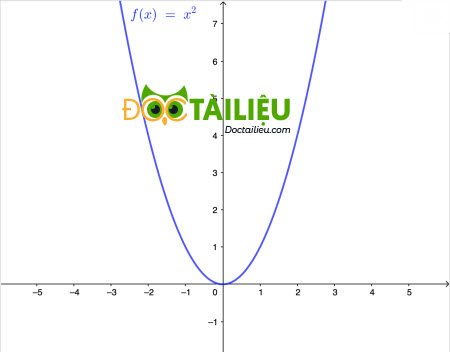
b)
Toạ độ điểm B là:
\(\left\{ \matrix{ x = -3 \hfill \cr y = x^2 = 9 \hfill \cr} \right.\)
Bài IV.
Gọi vận tốc xe máy là X, vận tốc ô tô là Y (km/h, X, Y > 0)
Theo bài ra ta có:
\(\left\{ \matrix{X = Y -10 \hfill \cr X.3 + Y.2 = 270 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{X = 50 \hfill \cr Y = 60 \hfill \cr} \right.\) (km/h)
KL....
Bài V.
1.
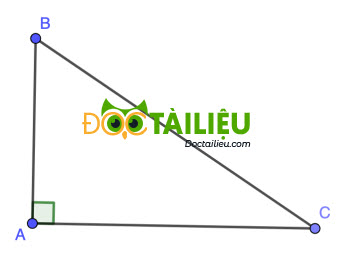
Áp dụng Pytago cho △ABC vuông tại A ta có:
\(AC = \sqrt{{BC}^2 - {AB}^2} = \sqrt{10^2 - 6^2} = 8\) (cm)
Ta có:
\(M = 3sin B + 2cos C = 3.\dfrac{AC}{BC} + 2.\dfrac{AC}{BC} =5.\dfrac{AC}{BC} = 5.\dfrac{8}{10} =4\).
2. Từ một điểm A ở ngoài đường tròn (O;R), vẽ hai tiếp tuyến AB và AC với đường tròn (B và C là hai tiếp điểm), gọi H là giao điểm của OA và BC.
a)
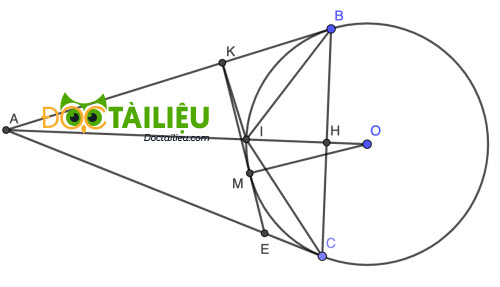
Vì AB và AC là 2 tiếp tuyến tại B và C của (O) ⇒ OB ⊥ BA và OC ⊥ CA hay ∠OBA = ∠OCA = 90°.
Xét △OBA và △OCA có:
∠OBA = ∠OCA = 90°
OB = OC ( = R)
OA chung
Suy ra △OBA = △OCA ⇒ ∠BOA = ∠COA hay OA là phân giác của góc BOC.
Xét △BOC có BO = CO = R ⇒ △BOC cân tại O, có OA là phân giác của góc O ⇒ OA ⊥ BC (đpcm).
b)
Vì ∠OBA = ∠OCA = 90° (cm pa) ⇒ B và C cùng thuộc đường tròn đường kính AO, hay bốn điểm A,O,B,C cùng thuộc một đường tròn (đpcm).
c)
Vì △BOC cân tại O có OH là đường cao (cm pa) ⇒ H là trung điểm BC.
Xét △IBC có IH vừa là trung tuyến vừa vuông góc với BC ⇒ △IBC cân tại I ⇒ ∠BCI = ∠CBI.
Theo tính chất góc tạo bởi tiếp tuyến AB và dây cung BI của (O) ta có:
∠KBI = ∠BCI = ∠CBI hay ∠KBI = ∠HBI.
Xét △HBI và △KBI có:
∠IHB = ∠IKB = 90°
∠KBI = ∠HBI (cmt)
IB chung
Suy ra △HBI = △KBI ⇒ IK = IH (đpcm).
d)
Áp dụng Pytago trong △OBA vuông tại B ta có:
\(AB = \sqrt{{OA}^2 - {OB}^2} = \sqrt{{(3R)}^2 - {R}^2} =R.2\sqrt2\)
Từ chứng minh phần a ta có △OBA = △OCA ⇒ AB = AC.
Chứng minh tương tự ý a, ta có KM = KB và EM = EC.
Ta có:
\(P_{\triangle AKE} = AK + KE + EA = AK +EA + KM + ME \)
\(= AK +EA + KB + EC = AB + AC = 2AB = 4\sqrt 2 .R \)
\(P_{\triangle AKE} =4\sqrt 2 .R \)
KL........
-/-
Đọc tài liệu vừa chia sẻ đến các em lời giải đề thi thử vào 10 môn Toán của tỉnh Tiền Giang năm 2020, còn rất nhiều bộ đề thi thử vào lớp 10 môn Toán của các trường khác trên cả nước đã được chúng tôi biên tập, thường xuyên truy cập vào trang để cập nhật nhé
