Trường THCS Võ Thị Sáu thuộc quận Lê Chân - Hải Phòng vừa tổ chức kỳ thi thử tuyển sinh vào lớp 10 dành cho các em học sinh khối lớp 9 với đề thi thử môn Toán như sau:
Đề thi
Bài 1. (1,5 điểm)
Cho hai biểu thức\(A = (4\sqrt 2 + \sqrt{30})(\sqrt 5 - \sqrt 3) \sqrt{4-\sqrt{15}}\)
và \( B = \left( \dfrac{x-y}{\sqrt x - \sqrt y} - \dfrac{\sqrt {x^3} - \sqrt {y^3}}{x-y} \right): \dfrac{(\sqrt {x} - \sqrt {y})^2+\sqrt{xy}}{\sqrt {x} + \sqrt {y}}\)
(với \(x \geq 0;y \geq 0;x≠y\))
1. Rút gọn hai biểu thức trên.
2. So sánh A và 2B.
Bài 2. (1,5 điểm)
1. Cho các đường thẳng (d1): y = 2x - 1;
(d2): y = (m - 2)x + m + 3
và (d3): y = -3x + 4.
Tìm m để ba đường thẳng trên cùng đi qua một điểm.
2. Giải hệ phương trình
\(\left\{ \matrix{ \dfrac{x+y}{xy} = 10 \hfill \cr \dfrac{2}x - \dfrac{3}y = -25 \hfill \cr} \right. \)
Bài 3. (2,5 điểm)
1. Cho phương trình bậc hai:
\(x^2 – 2(a + 1)x +a -4 =0\) (*)
a) Hãy tính hiệu các lập phương của hai nghiệm ở phương trình (*) khi a = 0
b) Tìm các giá trị của a để phương trình (*) có ít nhất một nghiệm âm
2. Một ca nô chạy xuôi dòng trên một khúc sông dài 90 ki-lô-mét, rồi chạy ngược dòng trở lại 36 ki-lô-mét. Thời gian ca nô chạy xuôi dòng ít hơn chạy ngược dòng là 1 giờ. Tính thời gian ca nô chạy xuôi dòng. Biết rằng trong một giờ, trên khúc sông đó một đám bèo tự trôi được 6 ki-lô-mét.
Bài 4. (3,5 điểm)
1. Cho tam giác nhọn ABC nội tiếp trong đường tròn tâm O có \(AB < AC\). Trên cung nhỏ AC lấy điểm M khác A thỏa \(MA <>. Vẽ đường kính MN của đường tròn (O) và gọi H, K lần lượt là hình chiếu vuông góc của A trên MB, MN. Chứng minh rằng:
a) Bốn điểm A, H, K, M cùng nằm trên một đường tròn.
b) AH.AK = HB.MK.
c) Khi điểm M di động trên cung nhỏ AC thì đường thẳng HK luôn đi qua một điểm cố định.
2. Nhà hát Cao Văn Lầu và Trung tâm triển lãm văn ĐH hóa nghệ thuật tỉnh Bạc Liêu có hình dáng 3 chiếc nón lá lớn nhất Việt Nam, mái nhà hình nón làm bằng vật liệu composite và được đặt hướng vào nhau. Em hãy tính diện tích xung quanh và thể tích của một mái hình nón đó biết đường kính là 45m và chiều cao là 24m (lấy π = 3,14 , kết quả làm tròn đến hàng đơn vị)
Bài 5. (1,0 điểm)
1. Chứng minh rằng với mọi a > 0 ta có: \(a +\dfrac{1}a \geq 2\).
2, Cho 3 số x, y, z thoả mãn \(x\geq 2019\); \(y\geq 2020\); \(z\geq 2021\). Tìm giá trị nhỏ nhất của biểu thức:
\(M = x + \dfrac{1}x - \dfrac{1}{2019} + y + \dfrac{1}y - \dfrac{1}{2020} + z + \dfrac{1}z - \dfrac{1}{2021}\)
Hết
Đừng quên còn rất nhiều tài liệu đề thi thử tuyển sinh vào lớp 10 tất cả các môn năm 2020 đợi các em thử sức đó!
Lời giải chi tiết
Dưới đây là giải chi tiết đề thi thử tuyển sinh lớp 10 môn Toán của trường THCS Võ Thị Sáu quận Lê Chân - Hải Phòng do Đọc tài liệu thực hiện:
Bài 1.
\(A = (4\sqrt 2 + \sqrt{30})(\sqrt 5 - \sqrt 3) \sqrt{4-\sqrt{15}}\)
và \( B = \left( \dfrac{x-y}{\sqrt x - \sqrt y} - \dfrac{\sqrt {x^3} - \sqrt {y^3}}{x-y} \right): \dfrac{(\sqrt {x} - \sqrt {y})^2+\sqrt{xy}}{\sqrt {x} + \sqrt {y}}\)
(với \(x \geq 0;y \geq 0;x≠y\))
1. Ta có:
\(A = (4\sqrt 2 + \sqrt{30})(\sqrt 5 - \sqrt 3) \sqrt{4-\sqrt{15}}\)
\(=\sqrt 2 (4 + \sqrt{15})(\sqrt 5 - \sqrt 3) \sqrt{4-\sqrt{15}}\)
\(= (4 + \sqrt{15})(\sqrt 5 - \sqrt 3) \sqrt{8-2\sqrt{15}}\)
\(= (4\sqrt 5 + 5\sqrt 3 -4\sqrt 3- 3 \sqrt 5) \sqrt{(\sqrt 5 - \sqrt 3)^2}\)
\(= (\sqrt 5 + \sqrt 3) (\sqrt 5 - \sqrt 3) = 5 - 3 =2\)
Với \(x \geq 0;y \geq 0;x≠y\), ta có:
\( B = \left( \dfrac{x-y}{\sqrt x - \sqrt y} - \dfrac{\sqrt {x^3} - \sqrt {y^3}}{x-y} \right): \dfrac{(\sqrt {x} - \sqrt {y})^2+\sqrt{xy}}{\sqrt {x} + \sqrt {y}}\)
\(= \left( \dfrac{(\sqrt x - \sqrt y)(\sqrt x + \sqrt y)}{\sqrt x - \sqrt y} - \dfrac{(\sqrt x - \sqrt y)(x+\sqrt{xy}+y)}{(\sqrt x - \sqrt y)(\sqrt x + \sqrt y)} \right): \dfrac{x+y-\sqrt{xy}}{\sqrt {x} + \sqrt {y}}\)
\(= \dfrac{(\sqrt x + \sqrt y)^2-(x+\sqrt{xy}+y)}{\sqrt x + \sqrt y} . \dfrac{\sqrt {x} + \sqrt {y}}{x+y-\sqrt{xy}}\)
\(=\dfrac{\sqrt{xy}}{x+y-\sqrt{xy}}\)
2. So sánh A và 2B.
Xét
\(2B - A =2.\dfrac{\sqrt{xy}}{x+y-\sqrt{xy}} - 2\)
\(=\dfrac{2\sqrt{xy}-2x-2y + 2\sqrt{xy}}{x+y-\sqrt{xy}}\)
\(=\dfrac{-2(x-2\sqrt{xy} + y)}{x+y-\sqrt{xy}}\)
\(=\dfrac{-2(\sqrt{x} -\sqrt{y})^2}{x+y-\sqrt{xy}} < 0\) với \(x \geq 0;y \geq 0;x≠y\)
\(\Leftrightarrow 2B <>
Bài 2.
1.
Để ba đường thẳng trên cùng đi qua một điểm thì m phải thỏa mãn:
\(\left\{ \matrix{ m - 2 ≠ 2 \hfill \cr m - 2 ≠ -3 \hfill \cr y = 2x - 1 \hfill \cr y = -3x + 4 \hfill \cr} \right.\)
⇒ m = 0
2.
\(\left\{ \matrix{ \dfrac{x+y}{xy} = 10 \hfill \cr \dfrac{2}x - \dfrac{3}y = -25 \hfill \cr} \right. \) (đkxđ \(x,y ≠0\))
\(\Leftrightarrow \left\{ \matrix{ \dfrac{1}x + \dfrac{1}y = 10 \hfill \cr \dfrac{2}x - \dfrac{3}y = -25 \hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{ \dfrac{1}x=1 \hfill \cr \dfrac{1}y = 9 \hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{ x = 1 \hfill \cr y = \dfrac{1}9 \hfill \cr} \right. \) (tm đkxđ)
KL....
Bài 3.
1.
a)
Với a = 0, ta có:
(*) \(\Leftrightarrow x^2 - 2 x - 4 = 0\)
\(\Leftrightarrow \left[ \matrix{ x = 1 + \sqrt{5} \hfill \cr x = 1 - \sqrt{5} \hfill \cr} \right. \)
Hiệu các lập phương của hai nghiệm của (*) là:
\(x_1^3 - x_2^3 = (x_1-x_2)(x_1^2 + x_1x_2 + x_2^2) = (x_1-x_2)[(x_1+x_2)^2-x_1x_2]\)
\(= (1 + \sqrt 5-1 + \sqrt 5)[(1+ \sqrt 5+1- \sqrt 5)^2-(1+ \sqrt 5)(1- \sqrt 5)]\)
\(=2 \sqrt 5(2^2+4) = 16 \sqrt 5\)
b)
Để (*) có nghiệm khi và chỉ khi:
\(\Delta' = (a+1)^2 - a + 4 = a^2 + a + 5 > 0\) với mọi a
Hay (*) luôn có hai nghiệm phân biệt:
\(\left\{ \matrix{ x_1 = (a+1) + \sqrt {\Delta'} \hfill \cr x_2 = (a+1) - \sqrt {\Delta'} \hfill \cr} \right. \)
Dễ thấy \(x_2 < x_1\), để (*) có ít nhất một nghiệm âm \(\Leftrightarrow x_2 < 0\)
\(\Leftrightarrow (a+1) - \sqrt {\Delta'} < 0\)
\(\Leftrightarrow (a+1) < \sqrt {\Delta'} \) (**)
Với \(a < -1\) thì \( x_2 < 0\) với mọi a.
Với \(a \geq -1\), ta có:
(**) \(\Leftrightarrow (a+1) ^2< \ {\Delta'} = a^2 +a + 5\)
\(\Leftrightarrow a<4\).
KL \(a<4\) thì (*) có ít nhất một nghiệm âm.
2.
Gọi thời gian ca nô chạy xuôi dòng là T (giờ, T > 0)
Ta có: \(v_{xuôi \space dòng} = 6\space km/h\).
Vận tốc lúc đi của ca nô là \(\dfrac{90}T\) (km/h)
Vận tốc lúc ngược dòng của ca nô là \(\dfrac{36}{T+1}\) (km/h)
Theo bài ra ta có:
\(\dfrac{90}T - 6 = \dfrac{36}{T+1} + 6\)
\(\Leftrightarrow 12T^2 - 42T - 90 = 0\)
\(\Leftrightarrow \left[ \matrix{ T = 5 \space (tm)\hfill \cr T = \dfrac{-3}2 \space (loại) \hfill \cr} \right. \)
KL...
Bài 4.
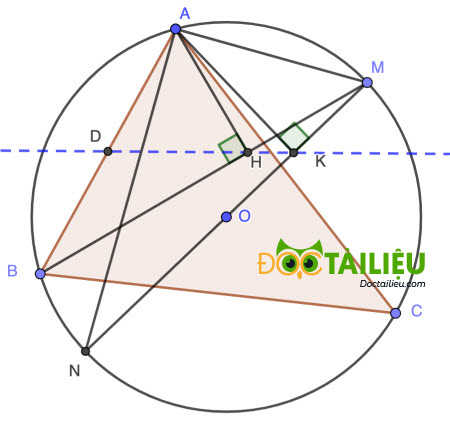
1.
a)
Vì H, K lần lượt là hình chiếu vuông góc của A trên MB, MN ⇒ AH ⊥ BM và AK ⊥ MN hay ∠AHM = ∠AKM = 90°
Suy ra H và K cùng thuộc đường tròn đường kính AM, hay bốn điểm A, H, K, M cùng nằm trên một đường tròn (đpcm).
b)
Vì MN là đường kính ⇒ ∠MAN = 90°.
Xét △MAN vuông tại A có AK là đường cao ⇒ ∠MAK = 90° - ∠AMK = ∠ANM.
Ta có:
∠ABM = ∠ANM (góc nội tiếp (O) cùng chắn cung AM) = ∠MAK (cmt).
Xét △AKM và △BHA ta có:
∠AHB = ∠AKM (= 90°)
∠ABM = ∠MAK (cmt)
Suy ra △AKM ∽ △BHA ⇒ \(\dfrac{AK}{KM} = \dfrac{BH}{HA}\) ⇒ AH.AK = HB.MK (đpcm).
c)
Gọi HK cắt AB tại D.
Vì △AKM ∽ △BHA (cm pb) ⇒ ∠BAH = ∠AMK
Lại có tứ giác AMKH nội tiếp (cm pa) ⇒ ∠AMK + ∠AHK = 180° ⇒ ∠AMK = 180° - ∠AHK = ∠AHD
⇒ ∠BAH = ∠AHD ( cùng = ∠AMK) ⇒ △ADH cân tại D ⇒ AD = DH.
Lại có: ∠DBH = 90° - ∠BAH = 90° - ∠AHD = ∠DHB ⇒ △BDH cân tại D ⇒ BD = DH = AD
Hay D là trung điểm của AB.
Vậy HK luôn đi qua điểm D là trung điểm của AB cố định (đpcm).
2.
Diện tích xung quanh của một mái hình nón là:
\(S_{xq} = \pi rl = \pi r \sqrt {r^2 + h^2 } = 3,14.22,5.\sqrt{{22,5}^2 + 24^2} ≈ 2324 \space (m^2)\)
Thể tích của một mái hình nón là:
\(V = \dfrac{1}3\pi r^2h = \dfrac{1}3.3,14 .{22,5}^2.24 =12717 \space (m^3)\)
KL.....
Bài 5.
1.
Vì a > 0 nên \(\sqrt a\) xác định.
Ta có:
\(a +\dfrac{1}a - 2 = \sqrt {a^2} + \dfrac{1}{\sqrt{a^2}} - 2.\sqrt {a.\dfrac{1}a} = \left( \sqrt {a} - \dfrac{1}{\sqrt{a}} \right)^2 \geq 0\) với mọi a > 0
hay \(a +\dfrac{1}a \geq 2\) (đpcm).
Dấu bằng xảy ra khi và chỉ khi \(a = \dfrac{1}a \Leftrightarrow a = 1\).
2,
Xét hàm số:
\(f(x) = x + \dfrac{1}x\)
Gọi \(x_1 > x_2 \geq 2019\), ta có:
\(f(x_1) - f(x_2)= x_1 + \dfrac{1}{x_1} - x_2 - \dfrac{1}{x_2} = (x_1-x_2)\left (1-\dfrac{1}{x_1x_2} \right)\)
\(\Leftrightarrow \dfrac{f(x_1) - f(x_2)}{x_1-x_2}=1-\dfrac{1}{x_1x_2} > 0\) (vì \(x_1 > x_2 \geq 2019\))
Suy ra f(x) là đồng biến với mọi \(x\geq 2019\).
Ta có:
\(M = x + \dfrac{1}x - \dfrac{1}{2019} + y + \dfrac{1}y - \dfrac{1}{2020} + z + \dfrac{1}z - \dfrac{1}{2021}\)
\(M = f(x) - \dfrac{1}{2019} + f(y) - \dfrac{1}{2020} +f(z)- \dfrac{1}{2021} \geq f(2019) - \dfrac{1}{2019} + f(2020) - \dfrac{1}{2020} +f(2021)- \dfrac{1}{2021}\)
\(\Leftrightarrow M \geq 2019 +\dfrac{1}{2019} - \dfrac{1}{2019} + 2020+\dfrac{1}{2020} - \dfrac{1}{2020} +2021+\dfrac{1}{2021} - \dfrac{1}{2021}\)
\(\Leftrightarrow M \geq 6060\).
Vậy \({Min}_M = 6060 \Leftrightarrow \) x = 2019; y = 2020; z = 2021.
-/-
Đọc tài liệu vừa chia sẻ đến các em lời giải đề thi thử vào 10 môn Toán của trường THCS Võ Thị Sáu năm 2020, còn rất nhiều bộ đề thi thử vào lớp 10 môn Toán của các trường khác trên cả nước đã được chúng tôi biên tập, thường xuyên truy cập vào trang để cập nhật nhé
