Cùng Đọc tài liệu thử sức với đề thi thử tuyển sinh vào 10 môn Toán dành cho các em học sinh lớp 9 năm học 2019-2020 do trường THCS Nha Trang (Thái Nguyên) ra đề:
Đề thi thử
|
PHÒNG GDĐT TP THÁI NGUYÊN TRƯỜNG THCS NHA TRANG |
THI THỬ TUYỂN SINH VÀO LỚP 10 THPT Năm học 2020 - 2021 MÔN THI: TOÁN Thời gian làm bài: 120 phút, không kể thời gian phát để |
Câu 1 (1.0 điểm).
Tìm x để căn thức sau có nghĩa: \(\sqrt{\dfrac{2020}{5-x}}\)Câu 2 (1.0 điểm). Không giải phương trình, hãy tính tổng và tích các nghiệm (nếu có) của phương trình: \(x^2-\dfrac{7}{3}x+\dfrac{2}{3} = 0\).
Câu 3 (1.0 điểm). Cho hàm số \(y=-2020x^2\). Khi \(2020
Câu 4 (1.0 điểm). Cho hàm số y=(-m +4)x + m - 1. Tìm các giá trị của m để hàm số đã cho là hàm số bậc nhất nghịch biến trên ℝ và đồ thị của hàm số đó cắt trục tung tại điểm có tung độ bằng 2020.
Câu 5 (1.0 điểm). Cho biểu thức
\(A = \left(\dfrac{x}{\sqrt{x}-2}-\dfrac{x-1}{\sqrt{x}+2}- \dfrac{\sqrt{x}+6}{x-4}\right): \left(\dfrac{\sqrt{x}+2}{\sqrt{x}-2}-1\right)\) với x ≥0 và x≠4
a) Rút gọn A.
b) Tìm giá trị của x để A dương,
Câu 6 (1.0 điểm). Hai dung dịch muối (dung dịch I, dung dịch II) có khối lượng tổng cộng bằng 100 kg. Khối lượng muối trong các dung dịch I, dung dịch II lần lượt là 3 kg và 1kg. Biết nồng độ muối trong dung dịch I nhiều hơn nồng độ muối trong dung dịch 1 là 2,5 %. Tỉnh khối lượng mỗi dung dịch nói trên.
Câu 7 (1.0 điểm).
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 5cm, AC = 12cm. Tính diện tích tam giác ACH.Câu 8 (1.0 điểm). Cho hình vuông ABCD. Vẽ đường tròn (O) đường kính AB và đường tròn (D;DC), chúng cắt nhau tại điểm M (M ≠ A). Đường thẳng BM cắt đoạn thẳng DC tại điểm N. Chứng minh N là trung điểm của DC.
Câu 9 (1.0 điểm). Cho tam giác ABC có ba góc nhọn (\(AB < AC\)) và có trực tâm H. Vẽ hình bình hành BHCD. Đường thẳng qua D song song với BC cắt đường thẳng AH tại M. Chứng minh các điểm A, B, M, D, C cùng thuộc một đường tròn.
Câu 10 (1.0 điểm). Cho tam giác ABC có ba góc nhọn (\(AB > AC\)) nội tiếp đường tròn tâm O. Gọi E, F lần lượt là hình chiếu vuông góc của C, B trên AB và AC. M, N lần lượt là trung điểm của các cạnh AB và AC, H là trực tâm của tam giác ABC.
a) Chứng minh AM.EF = AF.MN.
b) Gọi D, K, I lần lượt là giao điểm của các cặp đường thẳng EF và MN, AO và MN, AH và EF. Chứng minh K là trực tâm của tam giác DAI.
-Hết-
Như vậy Đọc tài liệu đã giới thiệu tới các em đề thi thử vào 10 môn Toán năm học 2020 - 2021 dành cho các em học sinh lớp 9 tại TP Thái Nguyên khá sát với cấu trúc và dạng đề thi môn toán đã cho của các năm trước, đừng quên tham khảo các đề thi thử vào lớp 10 các môn khác của tất cả các tỉnh thành trên cả nước do Đọc tài liệu tổng hợp nữa em nhé.
Lời giải chi tiết
Câu 1: (1,0 điểm)
Để căn thức sau có nghĩa: \(\sqrt{\dfrac{2020}{5-x}}\)
\(\Leftrightarrow \left\{ \matrix{ \dfrac{2020}{5-x} \geq 0 \hfill \cr 5-x ≠ 0 \hfill \cr} \right.\)
\(\Leftrightarrow 5-x > 0\) \(\Leftrightarrow x < 5\).
Câu 2: (1,0 điểm)
\(x^2 - \dfrac{7}{3}x +\dfrac{2}{3} =0\)
Ta có:
\(\Delta = \Big( \dfrac{7}{3} \Big)^2 - 4. \dfrac{2}{3} = \dfrac{25}{9} >0\)
\(\Rightarrow \) Phương trình đã cho luôn có hai nghiệm.
Áp dụng hệ thức Vi - ét cho phương trình đã cho, ta có:
\( \left\{ \matrix{ x_1 + x_2 = \dfrac{7}{3} \hfill \cr x_1x_2 =\dfrac{2}{3} \hfill \cr} \right.\)
Câu 3: (1,0 điểm)
Gọi \(y = f(x)= -2020x^2\).
Xét \(x_1\) và \(x_2\) sao cho \(2020
\(f(x_1)-f(x_2) = -2020x_1^2+2020x_2^2\)
\(= -2020(x_1 -x_2 )(x_1 +x_2 )\)
\(\Leftrightarrow \dfrac{f(x_1) - f(x_2)}{x_1-x_2} = -2020(x_1+x_2)\) \(< 0\) với \(2020
Suy ra hàm đã cho nghịch biết trong khoảng \(2020 <>
Câu 4: (1,0 điểm)
Đặt \(y=f(x) = (-m+4)x +m-1\).
Để hàm đã cho là hàm bậc nhất
Xét \(x_1\) và \(x_2\), \(x_1,x_2 ∈ ℝ\) ta có: \(\Leftrightarrow m ≠ 4\).
\(f(x_1)-f(x_2) = (-m+4)x_1 +m-1 - [(-m+4)x_2 +m-1]\)
\(= (-m+4)(x_1 -x_2)\)
\(\Leftrightarrow \dfrac{f(x_1) - f(x_2)}{x_1-x_2} = -m+4\).
Để hàm số đã cho nghịch biến trên ℝ
\(\Leftrightarrow \dfrac{f(x_1) - f(x_2)}{x_1-x_2} = -m+4 < 0\)
\(\Leftrightarrow m > 4\).
Vậy để hàm số đã cho là hàm số bậc nhất nghịch biến trên ℝ \(\Leftrightarrow m > 4\).
Để đồ thị của hàm số đó cắt trục tung tại điểm có tung độ bằng 2020
\(\Leftrightarrow \) \(2020=f(0) = (-m+4).0 +m-1\)
\(\Leftrightarrow m - 1 = 2020\) \( \Leftrightarrow m = 2021\).
Câu 5: (1,0 điểm)
Cho biểu thức:
a, Với \(x\geq 0\) và \(x ≠ 4\), ta có:
\(A = \Big(\dfrac{x}{\sqrt{x}-2} - \dfrac{x-1}{\sqrt{x}+2} - \dfrac{\sqrt{x}+6}{x-4} \Big) : \Big( \dfrac{\sqrt{x}+2}{\sqrt{x}-2} -1 \Big)\)
\(= \Big[ \dfrac{x(\sqrt{x}+2) - (x-1)(\sqrt{x}-2)-(\sqrt{x}+6)}{x-4} \Big] : \Big[ \dfrac{\sqrt{x}+2-(\sqrt{x}-2)}{\sqrt{x}-2} \Big]\)
\(= \Big( \dfrac{x\sqrt{x}+2x - x\sqrt{x}+2x+\sqrt{x}-2-\sqrt{x}-6}{(\sqrt{x}-2)(\sqrt{x}+2)} \Big): \dfrac{4}{\sqrt{x}-2} \)
\(= \dfrac{4x-8}{(\sqrt{x}-2)(\sqrt{x}+2)} . \dfrac{\sqrt{x}-2}{4} \)
\(= \dfrac{x-2}{\sqrt{x}+2} \)
b,
Để A dương
\(\Leftrightarrow\) \( \left\{ \matrix{ x \geq 0 \hfill \cr x≠4 \hfill \cr A= \dfrac{x-2}{\sqrt{x}+2} > 0\hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ x >2 \hfill \cr x≠4 \hfill \cr} \right.\).
Câu 6: (1,0 điểm)
Gọi khối lượng dung dịch I và II lần lượt là A và B (kg) (\(A,B>0\)).
Theo giả thiết ta có:
\( \left\{ \matrix{ A+B =100 \hfill \cr \dfrac{3}{A} - \dfrac{1}{B} = 2,5\% \hfill \cr } \right.\)
\(\Leftrightarrow\) \( \left\{ \matrix{ A =100 -B\hfill \cr \dfrac{3}{100-B} - \dfrac{1}{B} = \dfrac{1}{40} \hfill \cr } \right.\)
\(\Leftrightarrow\) \( \left\{ \matrix{ A =100 -B\hfill \cr 40.(3B - 100 + B) = (100-B).B \hfill \cr } \right.\)
\(\Leftrightarrow\) \( \left\{ \matrix{ A =100 -B\hfill \cr B^2 +60B - 4000 = 0 \hfill \cr } \right.\)
\(\Leftrightarrow\) \( \left\{ \matrix{ A =100 -B\hfill \cr \left[ \matrix{ B = 40 \hfill \cr B = -100 \hfill \cr} \right. \hfill \cr } \right.\)
Vì \(A,B>0\) \(\Rightarrow\) \(B = 40\) (kg)
\(\Leftrightarrow\) \(A = 100 - 40 = 60\) (kg).
Câu 7: (1,0 điểm)
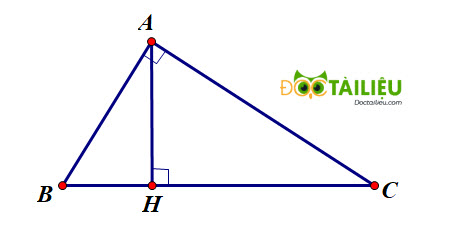
Áp dụng định lý Pytago cho tam giác ABC ta có:
\({BC}^2 = {AB}^2+ {AC}^2\) \(\Leftrightarrow\) \(BC = \sqrt{5^2 + 12^2} = 13\) (cm)
\(2S_{\triangle ABC } = AB.AC = AH.BC\)
\(\Leftrightarrow\) \(AH = \dfrac{AB.AC}{BC} = \dfrac{5.12}{13} = \dfrac{60}{13}\) (cm)
Áp dụng định lý Pytago cho tam giác AHC ta có:
\({HC}^2 = {AC}^2- {AH}^2\) \(\Leftrightarrow\) \(HC = \sqrt{12^2 - \Big(\dfrac{60}{13} \Big)^2} = \dfrac{144}{13}\) (cm)
Diện tích tam giác ACH là:
\(S_{\triangle ACH } = \dfrac{1}{2} AH.HC\)
\(= \dfrac{1}{2}.\dfrac{60}{13}.\dfrac{144}{13}\) \(= \dfrac{4320}{169} ≈ 25,562\) (cm²).
Câu 8: (1,0 điểm)
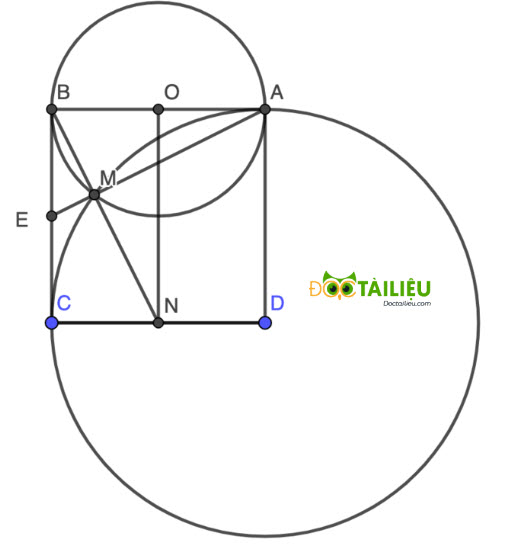
Gọi AM cắt BC tại E. Ta dễ thấy EB và EC lần lượt là tiếp tuyến tới (O) và (D) (do EB ⊥ BO tại B, EC ⊥ CD tại C).
Xét 2 tam giác EMB và EBA, ta có:
Góc BEA chung
∠EBM = ∠EAB (tính chất góc tạo bởi tiếp tuyến EB và dây cung BM)
Suy ra △EMB ∽ △EBA \(\Rightarrow\) \(\dfrac{EB}{EM} = \dfrac{EA}{EB} \)
\(\Rightarrow\) \({EB}^2 = EM.EA\) (1)
Chứng minh tương tự △EMC ∽ △ECA
\(\Rightarrow\) \({EC}^2 = EM.EA\) (2)
Từ (1) và (2) \(\Rightarrow\) \(EB =EC\) hay E là trung điểm BC.
Xét 2 tam giác BEM và BNC, ta có:
∠BCN = ∠EMB = 90⁰
Góc CBN chung
Suy ra △BEM ∽ △BNC \(\Rightarrow\) \(\dfrac{BE}{BM} = \dfrac{BN}{BC} \)
\(\Rightarrow\) \( BM.BN = BE.BC \) \( = \dfrac{1}{2}{BC}^2 \) \( = \dfrac{1}{2}{BA}^2 \) \( = BO.BA\)
\(\Rightarrow\) \(\dfrac{BM}{BO} = \dfrac{BA}{BN} \).
Xét 2 tam giác BMO và BAN, ta có:
Góc NBA chung
\(\dfrac{BM}{BO} = \dfrac{BA}{BN} \)
Suy ra △BMO ∽ △BAN \(\Rightarrow\) ∠NOA = ∠NMA = 90⁰
\(\Rightarrow\) NO // BC, lại có O là trung điểm AB \(\Rightarrow\) NO là đường trung bình của ABCD, hay N là trung điểm CD (đpcm).
Câu 9: (1,0 điểm)
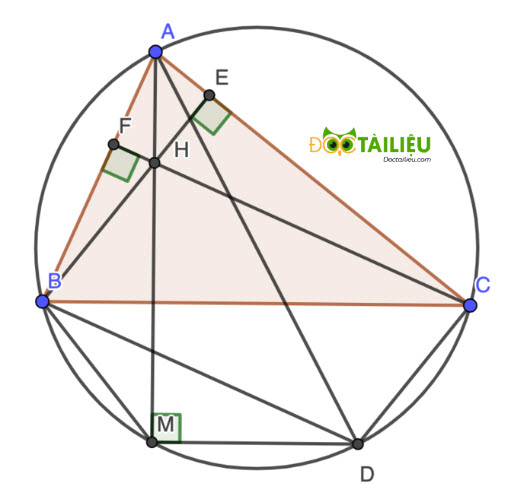
H là trực tâm △ABC \(\Rightarrow\) AH ⊥ BC, lại có DM // BC (gt) \(\Rightarrow\) AH ⊥ DM \(\Rightarrow\) ∠AMD = 90⁰ \(\Rightarrow\) M thuộc đường tròn đường kính AD (1).
Vì BHCD là hình bình hành \(\Rightarrow\) DB // CH, lại có CH ⊥ AB (do H là trực tâm △ABC) \(\Rightarrow\) DB ⊥ AB \(\Rightarrow\) ∠ABD = 90⁰ \(\Rightarrow\) B thuộc đường tròn đường kính AD (2).
Tương tự, vì BHCD là hình bình hành \(\Rightarrow\) DC // BH, lại có BH ⊥ AC (do H là trực tâm △ABC) \(\Rightarrow\) DC ⊥ AC \(\Rightarrow\) ∠ACD = 90⁰ \(\Rightarrow\) C thuộc đường tròn đường kính AD (3).
Từ (1), (2) và (3) suy ra B, M, C cùng thuộc đường tròn đường kính AD, hay 5 điểm A, B, M, D, C cùng thuộc đường tròn đường kính AD (đpcm).
Câu 10: (1,0 điểm)
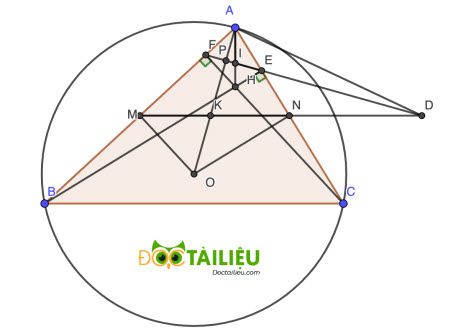
a,
Xét 2 tam giác AFC và AEB, ta có:
Góc BAC chung
∠AEB = ∠AFC = 90⁰
Suy ra △AFC ∽ △AEB \(\Rightarrow\) \(\dfrac{AF}{AC} = \dfrac{AE}{AB} \)
Mà M và N là trung điểm AB, AC \(\Rightarrow\) \(\dfrac{AF}{2.AN} = \dfrac{AE}{2.AM} \)
\(\Rightarrow\) \(\dfrac{AF}{AE} = \dfrac{AN}{AM} \)
Xét 2 tam giác AFE và ANM, ta có:
Góc BAC chung
\(\dfrac{AF}{AE} = \dfrac{AN}{AM} \)
Suy ra △AFE ∽ △ANM \(\Rightarrow\) \(\dfrac{AF}{EF} = \dfrac{AN}{MN} \)
\(\Rightarrow\) \(AN.EF = AF.MN\) (đpcm)
b,
H là trực tâm △ABC \(\Rightarrow\) AH ⊥ BC, lại có MN // BC (MN là đường trung bình △ABC) \(\Rightarrow\) AH ⊥ MN hay AI ⊥ DK (*)
Gọi AK cắt FD tại P.
Vì ∠AFH = ∠AEH = 90⁰ \(\Rightarrow\) Tứ giác AFHE nội tiếp đường tròn \(\Rightarrow\) ∠AFP = ∠AFE = ∠AHE (góc nội tiếp cùng chắn cung AE) = 90⁰ - ∠HAE
Vì M, N là trung điểm AB và AC \(\Rightarrow\) OM ⊥ AB và ON ⊥ AC \(\Rightarrow\) ∠OMA = ∠ONA = 90⁰ \(\Rightarrow\) Tứ giác AMON nội tiếp đường tròn \(\Rightarrow\) ∠FAP = ∠MAO = ∠MNO (góc nội tiếp cùng chắn cung AN) = 90⁰ - ∠MNA.
Cộng vế theo vế 2 biểu thức trên, ta có:
∠AFP + ∠FAP = 90⁰ - ∠HAE + 90⁰ - ∠MNA
⇔ 180⁰ - ∠AFP - ∠FAP = ∠HAE + ∠MNA
⇔ ∠FPA = ∠HAE + ∠MNA = 90⁰ (do AH ⊥ MN)
⇔ AP ⊥ FP hay AK ⊥ DI (**)
Từ (*) và (**), K là giao điểm AK và DK ⇒ K là trực tâm của tam giác DAI. (đpcm)
Trên đây là hướng dẫn giải chi tiết đề thi thử vào 10 môn toán năm 2020 lần 2 của TP Hồ Chí Minh. mong rằng đây sẽ là tài liệu hữu ích giúp các em ôn tập. Đừng quên còn rất nhiều tài liêu đề thi thử vào lớp 10 môn toán khác của các tỉnh thành trên cả nước nhé.
- Trọn bộ đề thi tuyển sinh lớp 10 môn toán 2019 chính thức của 63 tỉnh thành phố -
