Phòng GD&ĐT huyện Trực Ninh vừa tổ chức kỳ thi thử tuyển sinh vào lớp 10 dành cho các em học sinh khối lớp 9 với đề thi thử môn Toán như sau:
Đề thi
|
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO HUYỆN TRỰC NINH ĐỀ CHÍNH THỨC |
ĐỀ THI THỬ VÀO LỚP 10 TRUNG HỌC PHỔ THÔNG NĂM HỌC 2020 - 2021 Môn: Toán - Lớp 9 Ngày thi 02 tháng 7 năm 2020 (Thời gian làm bài 120 phút) |
Phần I. Trắc nghiệm (2,0 điểm)
Hãy viết vào bài làm chữ cái đứng trước phương án trả lời đúng:
Câu 1. Điều kiện xác định của biểu thức \(y = \sqrt{1-x^2}\) là
A. \(x ≠ ± 1\)
B. \(x > 1 \)
C. \(x < 1\)
D. \(-1 ≤ x ≤ 1\)
Câu 2. Trên cùng mặt phẳng tọa độ, số điểm chung của đồ thị hàm số y = x² và đồ thị hàm số y = 15x + 16 là
A. 0
B. 1
C. 2
D. 3
Câu 3. Hệ phương trình : \(\left\{ \matrix{ 2x - y = 3 \hfill \cr mx + 3y = 7 \hfill \cr} \right.\)
vô nghiệm khi
A. m = 2
B. m = -6
C. m ≠ -6
D. m ≠ 2
Câu 4. Phương trình x² + 2019x - 2020m = 0 (m là tham số, x là ẩn) có hai nghiệm trái dấu khi và chỉ khi
A. m = 2020
B. m ≠ 2020
C. \(m > 0\)
D. \(m < 0 \)
Câu 5. Ban An có hai giá sách với tổng số là 200 cuốn sách. Nếu chuyển 30 cuốn sách từ giá thứ nhất sang giá thứ hai thì số sách mỗi giá là như nhau. Số cuốn sách ở giá thứ nhất và giá thứ hai lần lượt là:
A. 130 và 70
B. 30 và 70
C. 100 và 30
D. 65 và 135
Câu 6. Các tia nắng mặt trời chiếu vào một chiếc tháp (hình vẽ), tạo với mặt đất một góc bằng 34° và bóng của cái tháp trên mặt đất dài 86 m. Chiều cao của tháp (làm tròn đến mét) là:

A. 58m
B. 51m
C. 70m
D. 118m
Câu 7. Cho (O; R) có dây AB = R√2. Số đo cung nhỏ AB là:
A. 30⁰
B. 45⁰
C. 60⁰
D. 90⁰
Câu 8. Hình trụ có bán kính đáy là 6cm, chiều cao là 5cm. Thể tích của hình trụ đó là
A. 60 cm³
B. 80 cm³
C. 180 cm³
D. 200 cm³
Phần II. Tự luận (8,0 điểm)
Bài 1. (1,5 điểm)
1. Rút gọn biểu thức:\( \dfrac{2+\sqrt{2}}{\sqrt{2}+1}+ \dfrac{15}{\sqrt{3}}+\sqrt{5-2\sqrt{6}}\)
2. Cho biểu thức \(A= \left(\dfrac{4-\sqrt{x}}{x-1}-\dfrac{\sqrt{x}}{\sqrt{x}+1}\right) : \dfrac{2-\sqrt{x}}{\sqrt{x}-1}\)
với x ≥ 0; x ≠ 1; x ≠ 4
Chứng minh A > 0.
Bài 2. (1,5 điểm)
Cho phương trình x² – 2x + m - 5 = 0 (1), (m là tham số, x là ẩn)
1. Giải phương trình với m= -2.
2. Với giá trị của m thì phương trình (1) có hai nghiệm phân biệt \(x_1, x_2\) thỏa mãn \(\dfrac{1}{x_1} + \dfrac{1}{x_2}=4\)
Bài 3. (1,0 điểm) Giải hệ phương trình
\(\left\{ \matrix{ x\sqrt{x}-3x\sqrt{y}+3y\sqrt{x} - y\sqrt{y}=0 \hfill \cr x^2 - 2\sqrt{xy} +y = 0 \hfill \cr} \right. \)
Bài 4. ( 3,0 điểm) Cho đường tròn (O) đường kính AD, từ một điểm M ở ngoài đường tròn (O) vẽ hai tiếp tuyến MA và MB (A, B là hai tiếp điểm). Gọi H là giao điểm của MO và AB, I là trung điểm của MH, K là giao điểm của AI và (O).
Chứng minh rằng:
a) △AHM ∽ △DBA
b) ∠BDH = ∠HAK
c) KB vuông góc với KM
Bài 5. (1,0 điểm)
a) Giải phương trình \(\sqrt{x+1}+ \sqrt{2x+3} + \sqrt{x^2 +7} = 9\)
b) Cho \(P = \sqrt{ab} + \sqrt{bc} + \sqrt{ca} - \sqrt{abc}\), với a, b, c là các số dương thỏa mãn \(a + b + c <2021\). Chứng minh \(P < 1011.\)
---Hết---
Xem thêm các tài liệu đề thi thử vào lớp 10 tất cả các môn ăm 2020 nữa em nhé!
Đáp án
Phần I. Trắc nghiệm:
| Câu 1 | D | Câu 5 | A |
| Câu 2 | C | Câu 6 | A |
| Câu 3 | B | Câu 7 | D |
| Câu 4 | C | Câu 8 | C |
Phần II. Tự luận:
Bài 1.
1.
\( \dfrac{2+\sqrt{2}}{\sqrt{2}+1}+ \dfrac{15}{\sqrt{3}}+\sqrt{5-2\sqrt{6}}\)
\(= \dfrac{(2+\sqrt{2})(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}+ \dfrac{5.3}{\sqrt{3}}+\sqrt{3-2\sqrt{2.3}+2}\)
\(= (2+\sqrt{2})(\sqrt{2}-1)+ 5\sqrt{3}+\sqrt{(\sqrt3 - \sqrt 2)^2}\)
\(= \sqrt{2}+ 5\sqrt{3}+\sqrt3 - \sqrt 2\)
\(= 6\sqrt{3}\)
2.
Với x ≥ 0; x ≠ 1; x ≠ 4 ta có:
\(A= \left(\dfrac{4-\sqrt{x}}{x-1}-\dfrac{\sqrt{x}}{\sqrt{x}+1}\right) : \dfrac{2-\sqrt{x}}{\sqrt{x}-1}\)
\(= \dfrac{4-\sqrt{x}-\sqrt{x}(\sqrt{x}-1)}{(\sqrt{x}-1)(\sqrt{x}+1)} . \dfrac{\sqrt{x}-1}{2-\sqrt{x}}\)
\(= \dfrac{-x +4}{(2-\sqrt{x})(\sqrt{x}+1)}\)
\(= \dfrac{(2-\sqrt{x})(2+\sqrt{x})}{(2-\sqrt{x})(\sqrt{x}+1)}\)
\(= \dfrac{2+\sqrt{x}}{\sqrt{x}+1}\) \(= 1+\dfrac{1}{\sqrt{x}+1}\)
Dễ thấy Với x ≥ 0; x ≠ 1; x ≠ 4 \(\Rightarrow \sqrt x + 1 > 0\) \(\Rightarrow 1+ \dfrac{1}{ \sqrt x + 1} > 0\)
Hay A > 0 (đpcm).
Bài 2.
Cho phương trình x² – 2x + m - 5 = 0 (1), (m là tham số, x là ẩn)
1.
Với m = -2, ta có:
(1) \(\Leftrightarrow x^2 -2x - 7 = 0\)
\(\Leftrightarrow \left[ \matrix{ {x} =1 + 2\sqrt 2 \hfill \cr {x} =1 - 2\sqrt 2\hfill \cr} \right.\)
2.
Để (1) có hai nghiệm phân biệt ⇔
\(\Delta' = 1^2 -m + 5 > 0 \leftrightarrow m < 6\).
Áp dụng hệ thức Vi-ét cho (1) ta có:
\(\left\{ \matrix{ x_1+x_2 = 2 \hfill \cr x_1x_2 = m-5 \hfill \cr} \right.\)
Ta có:
\(\dfrac{1}{x_1} + \dfrac{1}{x_2}=4\)
(đkxđ: \(x_1,x_2 ≠ 0 \Leftrightarrow x_1x_2 = m-5 ≠0 \Leftrightarrow m ≠5\))
\(\Leftrightarrow \dfrac{x_1+x_2}{x_1x_2} =4\) \(\Leftrightarrow \dfrac{2}{m-5} =4\) \(\Leftrightarrow m- 5 = \dfrac{1}{2}\) \(\Leftrightarrow m= \dfrac{11}{2}\) (tm..)
KL....
Bài 3.
\(\left\{ \matrix{ x\sqrt{x}-3x\sqrt{y}+3y\sqrt{x} - y\sqrt{y}=0 \space (1)\hfill \cr x^2 - 2\sqrt{xy} +y = 0 \space (2) \hfill \cr} \right. \)
ĐKXĐ: \(x,y \geq 0\)
Ta có:
(1) \(\Leftrightarrow x\sqrt{x}-3x\sqrt{y}+3y\sqrt{x} - y\sqrt{y}=0\)
\(\Leftrightarrow (\sqrt{x} - \sqrt{y})^3=0\)
\(\Leftrightarrow x = y\)
Thay x = y vào (2) ta có:
\(y^2 - 2\sqrt{y.y} +y = 0\)
\(\Leftrightarrow y^2 - y = 0\)
\(\Leftrightarrow \left[ \matrix{ y = 0 \Rightarrow x = 0 \hfill \cr y = 1 \Rightarrow x = 1 \hfill \cr} \right.\) (tm đkxđ).
KL.....
Bài 4.
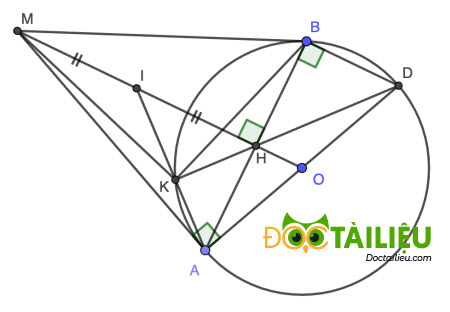
a)
Theo tính chất tiếp tuyến, ta có AB ⊥ OM tại H, H là trung điểm AB ⇒ ∠AHM = 90°.
Lại có ∠MAH = ∠MAB = ∠ADB (t/c góc tạo bởi tiếp tuyến và dây cung)
Xét △AHM và △DBA, ta có:
∠MAH = ∠ADB (cmt)
∠AHM = 90° = ∠DBA (góc nội tiếp chắn đường kính AD)
Suy ra △AHM ∽ △DBA (đpcm).
b)
Vì I là trung điểm HM ⇒ HM = 2HI.
Xét △OAB cân tại O (do OA = OB = R) có OH là đường cao ⇒ H là trung điểm AB ⇒ BA = 2BH.
Vì △AHM ∽ △DBA ⇒ \(\dfrac{AH}{HM} = \dfrac{BD}{BA}\) ⇔ \(\dfrac{AH}{2HI} = \dfrac{BD}{2BH}\) ⇔ \(\dfrac{AH}{HI} = \dfrac{BD}{BH}\).
Xét △AHI và △DBH, ta có:
\(\dfrac{AH}{HI} = \dfrac{BD}{BH}\) (cmt)
∠AHI = ∠DBH (= 90°)
Suy ra △AHI ∽ △DBH ⇒ ∠BDH = ∠HAI = ∠HAK (đpcm)
c)
Ta có ∠BAK = ∠BDK (góc nội tiếp (O) cùng chắn cung BK)
mà ∠BDH = ∠HAK = ∠BAK
Suy ra ∠BDH = ∠BDK hay 3 điểm K, H, D thẳng hàng.
Ta có ∠BKH = ∠BKD = ∠BAD (góc nội tiếp (O) cùng chắn cung BD) = 90° - ∠HAM = ∠AMH = ∠HMB
Hay ∠BKH = ∠BMH ⇒ tứ giác BMKH nội tiếp ⇒ ∠MKB = ∠MHB = 90°, hay KB ⊥ KM (đpcm).
Bài 5.
a) \(\sqrt{x+1}+ \sqrt{2x+3} + \sqrt{x^2 +7} = 9\)
(ĐKXĐ \(x \geq -1\))
\(\Leftrightarrow \sqrt{x+1} - 2+ \sqrt{2x+3} -3 + \sqrt{x^2 +7} -4 = 0\)
'\(\Leftrightarrow \dfrac{x-3}{\sqrt{x+1} +2}+ \dfrac{2x-6}{\sqrt{2x+3} +3}+ \dfrac{x^2-9}{ \sqrt{x^2 +7} +4} = 0\)
\(\Leftrightarrow (x-3)\left(\dfrac{1}{\sqrt{x+1} +2}+ \dfrac{2}{\sqrt{2x+3} +3}+ \dfrac{x+3}{ \sqrt{x^2 +7} +4} \right)= 0\)
Ta thấy \(\dfrac{1}{\sqrt{x+1} +2}+ \dfrac{2}{\sqrt{2x+3} +3}+ \dfrac{x+3}{ \sqrt{x^2 +7} +4} > 0 \) với mọi \(x \geq -1\)
Suy ra phương trình đã cho có một nghiệm duy nhất x = 3 (tm đkxđ).
b)
Theo nguyên tắc Dirichlet, trong 3 số \((\sqrt a -1)\); \((\sqrt b -1)\); \((\sqrt c -1)\) luôn tồn tại 2 số cùng dấu (cùng âm hoặc cùng dương).
Không mất tính tổng quát, ta giả sử 2 số đó là \((\sqrt a -1)\) và \((\sqrt b -1)\). Ta có:
\((\sqrt a -1)(\sqrt b -1) \geq 0\)
\(\Leftrightarrow \sqrt c(\sqrt a -1)(\sqrt b -1) \geq 0\)
\(\Leftrightarrow \sqrt {abc}-\sqrt {ac} -\sqrt {bc} + \sqrt c \geq 0\)
\(\Leftrightarrow \sqrt {ac} +\sqrt {bc} -\sqrt {abc} \leq \sqrt c\)
\(\Leftrightarrow P = \sqrt {ab}+\sqrt {ac} +\sqrt {bc} -\sqrt {abc} \leq \sqrt c + \sqrt {ab}\)
Áp dụng BĐT AM-GM cho cặp số (c;1) và (a;b), ta có:
\(\dfrac{c+1}2 \geq \sqrt c\)
\(\dfrac{a+b}2 \geq \sqrt {ab}\)
Cộng vế theo vế hai BĐT trên ta có:
\(P \leq \sqrt c + \sqrt {ab} \leq \dfrac{c+1}2+ \dfrac{a+b}2 = \dfrac{a+b+c+1}2 < \dfrac{2022}2\)
\(\Leftrightarrow P < 1011 \) (đpcm).
-/-
Đọc tài liệu vừa chia sẻ đến các em đề thi thử vào 10 môn Toán của huyện Trực Ninh năm 2020, còn rất nhiều bộ đề thi thử vào lớp 10 môn Toán của các trường khác trên cả nước đã được chúng tôi biên tập, thường xuyên truy cập vào trang để cập nhật nhé
