Đề thi minh họa vào 10 môn Toán Hải Phòng năm học 2021-2022

Sở GD&ĐT Hải Phòng chính thức công bố đề thi minh họa thi vào 10 môn Toán dành cho học sinh lớp 9 trên địa bàn tỉnh để giúp các em làm quen và thử sức với đề thi tại nhà. Đề thi chi tiết như sau:

Đề thi minh họa

vào 10 Hải Phòng

Bài 1 (1,5 điểm ) Cho hai biểu thức:

\(A=\sqrt{(\sqrt{5}-2)^{2}}+\dfrac{\sqrt{80}-5}{\sqrt{5}}\) ;

\(B=\dfrac{1}{3-\sqrt{x}}+\dfrac{\sqrt{x}}{3+\sqrt{x}}-\dfrac{x+9}{x-9}\) với \(x \geq 0, x \neq 9\)

1. Rút gọn các biểu thức A và B.

2. Tìm các giá trị của x để giá trị của biểu thức A và B thỏa mãn \(A=2 B^{2}\)

Bài 2 (1,5 điểm )

1. Giải hệ phương trình \(\left\{\begin{array}{l}4-2 x=3 y \\ x+y=-3\end{array}\right.\)

2. Bạn Nam hiện tại có 80000 (đồng). Để mua một quyển sách tham khảo môn Toán giá 260000 (đồng), bạn Nam lên kế hoạch mỗi ngày tiết kiệm 15000 (đồng). Gọi y (đồng) là tổng số tiền bạn Nam có sau x (ngày) thực hiện tiết kiệm.

a) Lập công thức tính y theo x.

b) Hỏi sau ít nhất bao nhiêu ngày bạn Nam có đủ tiền mua được quyển sách tham khảo môn Toán.

Bài 3 (2,5 điểm) 

1. Cho phương trình \(x^2 – 2m^2 - 4m – 5 = 0\) (m là tham số) (1)

a) Chứng minh rằng phương trình (1) luôn luôn có nghiệm với mọi giá trị của m.

b) Gọi \(x_1, x_2\) là các nghiệm của phương trình. Tìm các giá trị của m để biểu thức \(A = x_1^2 + x_2^2 - x_1x_2\) đạt giá trị nhỏ nhất.

2. Hưởng ứng phong trào “TẾT TRỒNG CÂY”, lớp 9A được phân công trồng 480 cây xanh. Số cây phải trồng được chia đều cho các bạn học sinh trong lớp. Tại buổi lao động trồng cây có 8 bạn vắng mặt. Để hoàn thành chỉ tiêu, mỗi bạn có mặt phải trồng thêm 3 cây nữa. Tính số học sinh của lớp 9A.

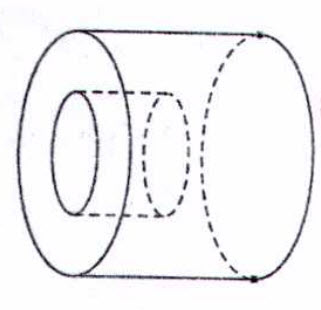
Bài 4 (0,75 điểm) Để chế tạo một chi tiết máy từ một khối kim loại hình trụ có bán kính của đường tròn đáy và chiều dài đều bằng 2r (cm), người ta khoan một lỗ cũng có dạng hình trụ với bán kính của đường tròn đáy và độ sâu bằng r(cm) (hình vẽ). Tính thể tích phần kim loại còn lại của chi tiết máy đó.

Bài 5 (3,0 điểm). Cho ba điểm A, B, C nằm trên đường thẳng xy theo thứ tự đó. Vẽ đường tròn (O) đi qua B và C ( O không nằm trên đường thẳng xy ). Từ điểm A vẽ hai tiến tuvến AM, AN của đường tròn (O) (M, N là các tiếp điểm ). Gọi E là hình chiếu của O trên xy.

a) Chứng minh năm điểm A, O, M, N, E cùng nằm trên một đường tròn. Xác dinh tâm của đường tròn đi qua năm điểm A, O, M, N, E.

b) Đường thẳng ME cắt đường tròn (O) tại I. Chứng minh IN song song với AB

c) Gọi K là giao điểm của MN và x y. Chứng minh AK.AE = AC.A B.

Bài 6 (0,75 Điểm) Cho các số \(x, y, z>1\) thoả mãn x + y + z = xyz. Tìm giá trị nhỏ nhất của biểu thức

\(P=\dfrac{y-2}{x^{2}}+\dfrac{z-2}{y^{2}}+\dfrac{x-2}{z^{2}}\)

Hết

Vậy là Đọc tài liệu đã giới thiệu tới các em đề thi minh họa tuyển sinh vào 10 2020 môn Toán của Hải Phòng, đừng quên còn rất nhiều tài liệu đề thi thử vào lớp 10 môn Toán khác đang đợi các em khám phá nhé!

Đáp án đề thi minh họa vào 10 Hải Phòng 2021

Bài 1 (1,5 điểm ) 

1. Ta có:

\(A=\sqrt{(\sqrt{5}-2)^{2}}+\dfrac{\sqrt{80}-5}{\sqrt{5}}\)

\(=(\sqrt{5}-2)+\dfrac{\sqrt{5}(4-\sqrt{5})}{\sqrt{5}}\)

\(=(\sqrt{5}-2)+(4-\sqrt{5}) = 2\)

Với \(x \geq 0, x \neq 9\), ta có:

\(B=\dfrac{1}{3-\sqrt{x}}+\dfrac{\sqrt{x}}{3+\sqrt{x}}-\dfrac{x+9}{x-9}\)

\(=\dfrac{3+\sqrt{x}+\sqrt{x}(3-\sqrt{x}) + x +9}{(3-\sqrt{x})(3+\sqrt{x})}\)

\(=\dfrac{12+4\sqrt{x}}{(3-\sqrt{x})(3+\sqrt{x})}\)

\(=\dfrac{4}{3-\sqrt{x}}\)

KL...

2. Với \(x \geq 0, x \neq 9\), để \(A=2 B^{2}\) ta có:

\(2=2 .\left(\dfrac{4}{3-\sqrt{x}}\right)^2\)

\(\Leftrightarrow \left(\dfrac{4}{3-\sqrt{x}}\right)^2 = 1\)

\(\Leftrightarrow \left[ \matrix{ \dfrac{4}{3-\sqrt{x}} = 1 \hfill \cr \dfrac{4}{3-\sqrt{x}} = -1 \hfill \cr} \right.\)

\(\Leftrightarrow \left[ \matrix{ 3-\sqrt{x} = 4 \hfill \cr 3-\sqrt{x} = -4 \hfill \cr} \right.\)

\(\Leftrightarrow \left[ \matrix{ \sqrt{x} = -1 \text{ (loại)}\hfill \cr \sqrt{x} = 7 \hfill \cr} \right.\)

\(\Rightarrow x = 49\) (tm đkxđ)

KL...

Bài 2 (1,5 điểm )

1. Ta có:

\(\left\{\begin{array}{l}4-2 x=3 y \\ x+y=-3\end{array}\right.\)

\(\Leftrightarrow \left\{\begin{array}{l}2x + 3y = 4 \\ x+y=-3\end{array}\right.\)

\(\Leftrightarrow \left\{\begin{array}{l}x = -13 \\ y= 10\end{array}\right.\)

KL...

2.

a)

Tổng số tiền Nam có sau x ngày tiết kiệm là:

\(y = 80000 + 15000x\)

b)

Để Nam đủ tiền mua sách thì cần số ngày tiết kiệm là x trong phương trình dưới:

\(260000 = 80000 + 15000x\)

\(\Leftrightarrow x = 12\) (ngày)

KL...

Bài 3 (2,5 điểm) 

1. Cho phương trình \(x^2 – 2m^2 - 4m – 5 = 0\) (m là tham số) (1)

a)

Ta có \((1) \Leftrightarrow x^2 = 2m^2 +4m + 5 = 2(m+1)^2 + 3 > 0\) với mọi m

Hay phương trình (1) luôn có nghiệm với mọi m (đpcm).

b) Gọi \(x_1, x_2\) là các nghiệm của phương trình. Tìm các giá trị của m để biểu thức \(A = x_1^2 + x_2^2 - x_1x_2\) đạt giá trị nhỏ nhất.

Áp dụng hệ thức Vi-ét cho (1) ta có:

\(\left\{\begin{array}{l}x_1+x_2 = 0 \\ x_1x_2 = -2m^2-4m-5 \end{array}\right.\)

Thay vào A ta có:

\(A = x_1^2 + x_2^2 - x_1x_2\)

\(= (x_1 + x_2)^2 - 3x_1x_2\)

\(= 0 - 3(-2m^2-4m-5)\)

\(= 6m^2+12m+15\)

\(= 6(m+1)^2 + 9 \geq 9 \) với mọi m.

Vậy min A = 9 ⇔ m = -1.

2.

Gọi số học sinh lớp 9A là X (học sinh, X ∈ ℕ)

Số cây mà mỗi bạn phải trồng ban đầu là: \(\dfrac{480}X\) (cây)

Số cây mà mỗi bạn phải trồng để hoàn thành chỉ tiêu sau khi có 8 bạn vắng mặt là:

\(\dfrac{480}X + 3 = \dfrac{480}{X-8}\)

\(\Leftrightarrow 480 (X-8) + 3X(X-8) = 480 X\)

\(\Leftrightarrow 3X^2 -24X - 3840 = 0\)

\(\Leftrightarrow \left\{ \matrix{ X = 40 \text{ (tm)} \hfill \cr X = -32 \text{ (loại vì X ≥ 0)} \hfill \cr} \right.\)

KL...

Bài 4 (0,75 điểm) 

Thể tích của cả hình hình trụ là:

\(V_1 = 2r. π(2r)^2 = 8 πr^3\) (cm³)

Thể tích phần hình trụ bị khoan là:

\(V_2 = r.πr^2 = πr^3\) (cm³)

Thể tích phần kim loại còn lại của chi tiết máy đó là:

\(V= V_1 - V_2 = 8 πr^3 - πr^3 = 7πr^3\) (cm³)

KL...

Bài 5 (3,0 điểm). Cho ba điểm A, B, C nằm trên đường thẳng xy theo thứ tự đó. Vẽ đường tròn (O) đi qua B và C ( O không nằm trên đường thẳng xy ). Từ điểm A vẽ hai tiến tuvến AM, AN của đường tròn (O) (M, N là các tiếp điểm ). Gọi E là hình chiếu của O trên xy.

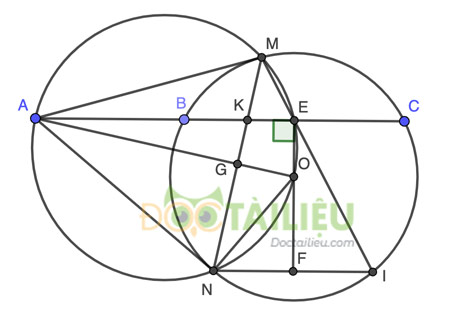
a)

Vì AM, AN là tiếp tuyến tới (O) nên ∠AMO = ∠ANO = 90°.

Lại có E là hình chiếu của O trên xy nên ∠AEO = 90°

Suy ra năm điểm A, O, M, N, E cùng nằm trên đường tròn đường kính AO, tâm đường tròn chính là trung điểm của AO (đpcm).

b)

Gọi EO cắt IN tại F.

Ta có: ∠AEI + ∠NIE = ∠AEO + ∠FEI + ∠NIE = 90° + (180° - ∠EFI) = 90° + 90° = 180°

Suy ra AE // NI hay IN // AB (đpcm).

c)

Gọi AO cắt MN tại G.

Dễ thấy ∠KGO = ∠KEO = 90° ⇒ tứ giác KGOE nội tiếp

Dễ chứng minh △AKG ~ △AOE ⇒ \(\dfrac{AK}{AG} = \dfrac{AO}{AE}\) ⇒ AK.AE = AG.AO  (1)

Áp dụng hệ thức lượng trong tam giác vuông AMO có đường cao MG, ta có AM² = AG.AO  (2)

Tương tự, vì AM là tiếp tuyến của (O) ta có △AMB ~ △ACM ⇒ \(\dfrac{AM}{AB} = \dfrac{AC}{AM}\) ⇒ AM² = AB.AC  (3)

Từ (1) (2) và (3) suy ra AK.AE = AC.AB (đpcm).

Bài 6 (0,75 Điểm) Cho các số \(x, y, z>1\) thoả mãn x + y + z = xyz. Tìm giá trị nhỏ nhất của biểu thức

\(P=\dfrac{y-2}{x^{2}}+\dfrac{z-2}{y^{2}}+\dfrac{x-2}{z^{2}}\)

\(\begin{aligned} &\Rightarrow \frac{1}{x y}+\frac{1}{y z}+\frac{1}{z x}=1\\ &\text { Ta có }\\ &P = \sum \frac{(x-1)+(y-1)}{x^{2}}-\sum \frac{1}{x}\\ &=\sum(x-1)\left(\frac{1}{x^{2}}+\frac{1}{z^{2}}\right)-\sum \frac{1}{x}\\ &\geq \sum(x-1) \cdot \frac{2}{x z}-\sum \frac{1}{x}\\ &=\sum \frac{1}{x}-2 \sum \frac{1}{x z} \geq \sqrt{3 \sum \frac{1}{x z}}-2 \sum \frac{1}{x z}=\sqrt{3}-2\\ &\text { dấu = xảy ra khi } x=y=z=\sqrt{3} \end{aligned}\)

Vậy là Đọc tài liệu đã cung cấp đáp án đề thi minh họa tuyển sinh vào 10 môn Toán tỉnh Hải Phòng năm học 2021/2022, đây chắc chắn là một tài liệu hữu ích giúp các em ôn luyện giải đề cũng nhưng các dạng toán có thể gặp trong kỳ thi tuyển sinh vào lớp 10 các năm. Chúc các em học tốt.

Tải ảnh đề thi: