Sở GD&ĐT Khánh Hòa vừa công bố đề thi tuyển sinh vào lớp 10 tham khảo môn Toán năm học 2020/2021 môn Toán như sau:
Đề thi minh họa
|
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA ĐỀ THI MINH HỌA (Đề thi có 01 trang) |
TUYỂN SINH VÀO LỚP 10 THPT NĂM HỌC 2020 – 2021 ĐỀ THI MINH HỌA Môn thi: TOÁN (Thời gian làm bài: 120 phút – không kể thời gian phát đề) |
Bài 1. (2,0 điểm)
Không dùng máy tính cầm taya) Giải phương trình x² - 6x + 5 = 0.
b) Rút gọn biểu thức \(M=(3\sqrt{50} -5\sqrt{18} +3\sqrt{8}). \sqrt{2}\).
Bài 2. (2,5 điểm) Trong mặt phẳng tọa độ Oxy cho đường thẳng (d): \(y= x + m-1\) và parabol (P): \(y = -x²\)?
a) Vē parabol (P): y = -x².
b) Tìm m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có hoành độ lần lượt là \(x_1, x_2\) thỏa mãn \(4(\dfrac{1}{x_1}+\dfrac{1}{x_2})+x_1x_2+3= 0.\)
Bài 3. (1,5 điểm)
Để chuẩn bị cho một xe hàng từ thiện chống dịch COVID-19, hai thanh niên cần chuyển một số lượng thực phẩm lên xe. Nếu người thứ nhất chuyển xong một nửa số lượng thực phẩm, và sau đó người thứ hai chuyến hết số còn lại lên xe thì thời gian người thứ hai hoàn thành lâu hơn người thứ nhất là 1 giờ. Nếu cả hai cùng làm chung thì thời gian chuyển hết số lượng thực phẩm lên xe là \(\dfrac{4}{3}\) giờ. Hỏi nếu làm riêng một mình thì mỗi người chuyển hết số lượng thực phẩm đó lên xe trong thời gian bao lâu?
Bài 4. (3,0 điểm)
Cho đường tròn tâm O, đường kính AB. Trên tiếp tuyến của đường tròn (O) tại A lấy điểm C (C≠A). Từ C vẽ tiếp tuyến thứ hai CD với đường tròn (O) (D là tiếp điểm). Kẻ DK vuông góc với AB(K ∈ AB), CB cắt đường tròn (O) tại điểm thứ hai là M và cắt DK tại N. Chứng minh rằng:
a) Tứ giác AMNK nội tiếp đường tròn.
b) AC² = CM.CB.
c) ∠MAD= ∠OCB.
d) N là trung điểm của DK.
Bài 5. (1,0 điểm)
Cho x là số thực dương. Tim giá trị nhỏ nhất của biểu thức \(A = 9x + \dfrac{1}{9x} - \dfrac{6\sqrt{x}+8}{x+1} + 2020\)
Hết
Đáp án đề thi minh họa vào 10 Khánh Hòa 2020
Bài 1.
a) \(x^2 - 6x + 5 = 0\)
⇔ \(x^2 - x - 5x + 5 = 0\)
⇔ \(x(x - 1) - 5 (x-1) = 0\)
⇔ \((x-1)(x-5)= 0\)
⇔ \(\left[ \begin{align}& x-1=0 \\& x-5=0 \\\end{align} \right.\\\)
⇔\(\left[ \begin{align}& x=1 \\& x=5 \\\end{align} \right.\\\)
KL: ...
b) \(M=(3\sqrt{50} -5\sqrt{18} +3\sqrt{8}). \sqrt{2}\)
⇔ \(M=(15\sqrt{2} -15\sqrt{2} +6\sqrt{2}). \sqrt{2}\)
⇔ \(M=12\)
KL: ...
Bài 2.
a) Các em kẻ bảng rồi vẽ parabol (P): y = -x².
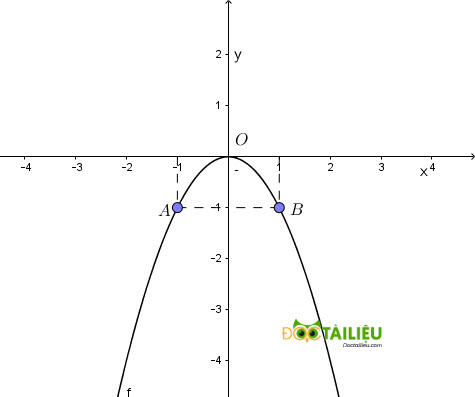
b) Giao điểm của đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có hoành độ lần lượt là \(x_1, x_2\) là nghiệm của phương trình:
\(x + m - 1 = -x²\)
⇔ \(x² + x + m - 1 = 0 (*)\)
Điều kiện để (*) có hai nghiệm phân biệt \(x_1, x_2\) là:
\(△ = 1^2 - 4.1.(m-1) >0 ⇔ m <1\)
Theo định lý Viet ta có:
\(\left\{ \matrix{ x_1+x_2 = -1 \hfill \cr x_1x_2 = m-1 \hfill \cr} \right. \) (1)
mà theo bài ta có \(x_1, x_2\) thỏa mãn \(4(\dfrac{1}{x_1}+\dfrac{1}{x_2})+x_1x_2+3= 0\)
⇔ \(4(\dfrac{x_1+x_2}{x_1x_2})+x_1x_2+3= 0\)
thay (1) vào ta được phương trình chứa tham số m
\(4(\dfrac{-1}{m-1})+m-1+3= 0\)
⇔ \(\dfrac{-4 + (m+2)(m-1)}{m-1}= 0\) (thêm điều kiện m ≠ 1)
⇔ \(m^2 + m - 6 =0\)
⇔ \((m-2) (m+3)=0\)
⇔\(\left[ \begin{align}& m=2 (loại) \\& m=-3 (t/m)\\\end{align} \right.\\ \)
KL: ...
Bài 3.
Gọi thời gian người thứ nhất chuyển hết số lương thực thực phẩm lên xe là x (giờ), thời gian người thứ nhất chuyển hết số lương thực thực phẩm lên xe là y (giờ) (điều kiện \(x, y >1\))
Theo bài ta sẽ có hệ phương trình sau:
\(\left\{ \matrix{ \dfrac{x}{2} + 1 = \dfrac{y}{2} \hfill \cr \dfrac{1}{x} + \dfrac{1}{y} = \dfrac{3}{4} \hfill \cr} \right.\)⇔\(\left[ \begin{align}& y= \dfrac{2}{3} (loại)\\& y=4 ⇒ x =2 \\\end{align} \right.\\\)
KL: ...
Bài 4.
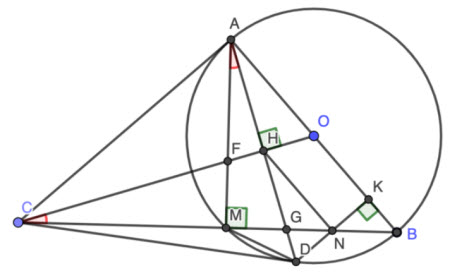
a, Ta có DK ⊥ AB ⇔ \(\angle NKA = 90⁰\)
Xét \(\triangle ABM\) nội tiếp đường tròn (O) có AB là đường kính ⇔ \(\angle AMB = 90⁰\)
Tứ giác AMNK có \(\angle AMB=\angle AKN = 90⁰\) ⇔ Tứ giác AMNK nội tiếp (đpcm)
b, Xét \(\triangle CAM\) và \(\triangle CBA\) ta dễ thấy:
\(\left\{ \matrix{ \angle ACB \space chung \hfill \cr \angle CMA = \angle CAB = 90⁰ \hfill \cr} \right.\) ⇔ \(\triangle CAM ∽ \triangle CBA\)
\(\Rightarrow \frac{CA}{CM}=\frac{CB}{CA}\)\(\Leftrightarrow CA^2 = CM.CB\) (đpcm)
c, Gọi OC cắt AM và AD lần lượt tại F và H, AD cắt CB tại G (như hình vẽ)
Ta thấy OC ⊥ AD ⇔ \(\angle FHG = 90⁰\)
Xét \(\triangle CHG \) và \(\triangle AMG \) ta có
\(\left\{ \matrix{ \angle CGA \space chung \hfill \cr \angle FHG=\angle FMG = 90⁰ \hfill \cr} \right.\)
⇔ \(\triangle CHG ∽ \triangle AMG\)\(\Rightarrow \angle GCH = \angle GAM\) hay \(\angle OCB = \angle MAD\) (đpcm)
d, Kẻ HN
Vì KN // AC (cùng ⊥AB)\(\Rightarrow \frac{CN}{CB}=\frac{AK}{AB}\) (1)
Dễ chứng minh \(\triangle CHA ∽ \triangle AKD\)
\(\Rightarrow \frac{CH}{AK}=\frac{CA}{AD}\) (2)
Tương tự \(\triangle COA ∽ \triangle ABD\)
\(\Rightarrow \frac{CO}{AB}=\frac{CA}{AD}\) (3)
Từ (2) và (3) \(\Rightarrow \frac{CH}{AK}=\frac{CO}{AB}\) \(\Rightarrow \frac{CH}{CO}=\frac{AK}{AB}\), kết hợp với (1) \(\Rightarrow \frac{CH}{CO}=\frac{AK}{AB}=\frac{CN}{CB}\) \(\Rightarrow \) HN // OB
\(\Rightarrow \frac{DN}{DK}=\frac{DH}{DA} = \frac{1}{2}\) (H là trung điểm AD) \(\Rightarrow \) N là trung điểm của DK (đpcm)
Bài 5.
\(A = 9x + \frac{1}{9x}-\frac{6\sqrt{x}+8}{x+1}+2020\)
ĐKXĐ: \(x >0\)
Ta đi chứng minh \(A \geq 2013\). Thật vậy:
\(A \geq 2013\) \(\Leftrightarrow \) \(9x + \frac{1}{9x}-\frac{6\sqrt{x}+8}{x+1}+2020 \geq 2013\)
\(\Leftrightarrow \)
\(9x + \frac{1}{9x}-\frac{6\sqrt{x}+8}{x+1}+7 \geq 0\)\(\Leftrightarrow \) \(9x + \frac{1}{9x} - 2 -\frac{6\sqrt{x}+8}{x+1}+9 \geq 0\)
\(\Leftrightarrow \) \((3\sqrt{x} - \frac{1}{3\sqrt{x}})^2+ \frac{9x+9 -(6\sqrt{x}+8)}{x+1} \geq 0\)
\(\Leftrightarrow \) \((3\sqrt{x} - \frac{1}{3\sqrt{x}})^2+ \frac{9x -6\sqrt{x}+1}{x+1} \geq 0\)
\(\Leftrightarrow \) \((3\sqrt{x} - \frac{1}{3\sqrt{x}})^2+ \frac{(3\sqrt{x} -1)^2}{x+1} \geq 0\) Luôn đúng với mọi \(x >0\)
\(\Leftrightarrow \) \(A \geq 2013\) (đpcm)
Dấu bằng xảy ra \(\Leftrightarrow \) \(\left\{ \matrix{ 3\sqrt{x} - \frac{1}{3\sqrt{x}}=0 \hfill \cr 3\sqrt{x} -1 =0 \hfill \cr} \right.\) \(\Leftrightarrow \) \(x=\frac{1}{9}\) (thoả mãn ĐKXĐ)
Vậy \(min \space A = 2013\) \(\Leftrightarrow \) \(x=\frac{1}{9}\)
-/-
Trên đây là đáp án đề thi minh họa tuyển sinh môn Toán vào 10 Khánh Hòa năm 2020, mong rằng với nội dung này các em sẽ thử sức đề thi thử vào lớp 10 2020 môn toán và ôn luyện kiến thức thật tốt!
