Cùng Đọc tài liệu thử sức với đề thi thử tuyển sinh vào lớp 10 môn toán năm 2020 lần 2 của huyện Mê Linh (Hà Nội) vừa diễn ra ngày 23/6 em nhé:
Đề thi thử
|
PHÒNG GD&ĐT MÊ LINH ĐỀ CHÍNH THỨC |
ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC SINH LỚP 9 NĂM HỌC 2019-2020 (ĐỢT 2) MÔN: TOÁN Thời gian làm bài 120 phút (không kể thời gian phát đề) |
Câu 1: (2,0 điểm).
Tính giá trị của các biểu thức sau:a) \(A = \sqrt{16+9}-2\)
b) \(B = \sqrt{(\sqrt{3}-1)^2}+1\)
Câu 2: (1,5 điểm) Cho biểu thức
\(P = \left(\dfrac{x-6}{x+3\sqrt{x}} - \dfrac{1}{\sqrt{x}}+ \dfrac{1}{\sqrt{x}+3} \right): \dfrac{2\sqrt{x}-6}{x+1}\)
với x > 0; x ≠ 9.
a) Rút gọn biểu thức P;
b) Tìm giá trị của x để P =1.
Câu 3: (2,5 điểm)
Cho đường thẳng \((d1): y = x+2\) và đường thẳng \((d2): y=(2m^2 - m)x + m^2 + m\) (m là tham số).
a) Tim m để (d1) // (d2)
b) Gọi A là điểm thuộc đường thẳng (d1) có hoành độ x = 2, Viết phương trình đường thẳng (d3) đi qua A vuông góc với (d1).
c)* Khi (d1) // (d2). Hãy tính khoảng cách giữa hai đường thẳng (d1), (d2)
d)* Tính khoảng cách từ gốc tọa độ 0 đến đường thẳng (d1) và tính diện tích tam giác OMN với M, N lần lượt là giao điểm của (d1) với các trục tọa độ Ox, Oy.
Câu 4: (2,0 điểm). Cho phương trình \(x^2 – 2x + m – 3 = 0\) (1) với m là tham số.
a) Giải phương trình (1) khi m = 0;
b) Tìm tất cả các giá trị của m để phương trình (1) có hai nghiệm phân biệt \(x_1, x_2\) thỏa mãn: \(x_1^2+12=2x_2-x_1.x_2\)
Câu 5: (3,0 điểm). Cho (O) đường kính AB = 2R, C là trung điểm của OA và dây MN vuông góc với OA tại C. Gọi K là điểm tùy ý trên cung nhỏ BM (K khác B, M ), H là giao điểm của AK và MN.
a) Chứng minh rằng BCHK là tứ giác nội tiếp.
b) Chứng minh AH.AK = AM²
c)* Xác định vị trí của điểm K để KM + KN + KB đạt giá trị lớn nhất và tính giá trị lớn nhất đó.
Hết
Trên đây là 5 câu hỏi trong đề thi thử lớp 10 mới nhất của huyện Mê Linh (Hà Nội) với môn Toán, cùng làm bài thi này trong 120 phút rồi đối chiếu với đáp án chi tiết dưới đây em nhé:
Lời giải chi tiết
Câu 1:
a) \(A = \sqrt{16+9}-2\) \(=3\)
b) \(B = \sqrt{(\sqrt{3}-1)^2}+1 = (\sqrt{3}-1)+1 = \sqrt{3}\)
Câu 2:
a)
Với x > 0; x ≠ 9, ta có:
\(P = \left(\dfrac{x-6}{x+3\sqrt{x}} - \dfrac{1}{\sqrt{x}}+ \dfrac{1}{\sqrt{x}+3} \right): \dfrac{2\sqrt{x}-6}{x+1}\)
\(= \left(\dfrac{x-6- \sqrt{x} - 3 + \sqrt{x}}{(\sqrt{x}+3)\sqrt{x}} \right).\dfrac{x+1}{2\sqrt{x}-6}\)
\(= \dfrac{x-9}{(\sqrt{x}+3)\sqrt{x}} .\dfrac{x+1}{2(\sqrt{x}-3)}\)
\(= \dfrac{x+1}{2\sqrt{x}}\)
b)
Để P = 1 \(\Leftrightarrow \dfrac{x+1}{2\sqrt{x}} = 1\) \(\Leftrightarrow {x+1}={2\sqrt{x}} \) \(\Leftrightarrow \sqrt{x} = 1 \Leftrightarrow x = 1\) (tm đkxđ).
Câu 3:
a)
Để (d1) // (d2) ⇔
\(\left\{ \matrix{ 2m^2-m = 1 \hfill \cr m^2 + m ≠ 2 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ m =1 ∨ m =\dfrac{-1}2 \hfill \cr m ≠ 1 \space và \space m≠-2 \hfill \cr} \right.\)
\(\Rightarrow m =\dfrac{-1}2\).
KL.....
b)
Tung độ điểm A là \(y = 2+ 2 = 4\) \(\Rightarrow A(2;4)\).
Phương trình (d3) đi qua A vuông góc với (d1) có dạng:
\(y - y_A = -1(x-x_A)\)
\(\Leftrightarrow y = -x + 6\)
c)*
Để (d1) // (d2) \(\Rightarrow m =\dfrac{-1}2\) (cmt), suy ra phương trình đường thẳng (d2) có dạng:
\((d2): y=\left[ 2\left( \dfrac{-1}2 \right)^2 - \left( \dfrac{-1}2 \right) \right]x + \left( \dfrac{-1}2 \right)^2 + \left( \dfrac{-1}2 \right)\)
\(\Leftrightarrow y=x - \dfrac{1}4 \)
Có điểm A(2;4) thuộc (d1) và (d1) // (d2) nên ta có:
Khoảng cách giữa (d1) và (d2) là
\(d_{(d_1;d_2)} = d_{(A;d_2)} = \dfrac{\left|2-4 - \dfrac{1}4\right|}{\sqrt{1^2+1^2}} = \dfrac{9\sqrt 2}8\)
d)*
\( d_{(O;d_1)} = \dfrac{\left|0-0+2\right|}{\sqrt{1^2+1^2}} = \sqrt 2\)
Toạ độ điểm M là giao điểm của (d1) với Ox là: \(\left\{ \matrix{ x_M = y_M - 2 = -2 \hfill \cr y_M = 0 \hfill \cr} \right.\)
Toạ độ điểm N là giao điểm của (d1) với Oy là: \(\left\{ \matrix{ x_M = 0 \hfill \cr y_M = x_M + 2 = 2 \hfill \cr} \right.\)
Ta có diện tích tam giác OMN là:
\(S_{\triangle OMN} = \dfrac{1}2.OM.ON = \dfrac{1}2 . |x_M|.|y_N| = \dfrac{1}2 . 2.2 =2\).
Câu 4:
a)
Với m = 0, ta có:
(1) \(\Leftrightarrow x^2 – 2x – 3 = 0\)
\(\Leftrightarrow \left[ \matrix{ {x} = 3 \hfill \cr {x} = -1 \hfill \cr} \right.\)
b)
Để (1) có hai nghiệm phân biệt
⇔ \(\Delta' = 1 - m + 3 > 0\) \(\Leftrightarrow m < 4\).
Áp dụng hệ thức Vi-ét cho (1), ta có:
\(\left\{ \matrix{ x_1+ x_2 = 2\hfill \cr x_1 x_2 = m-3 \hfill \cr} \right.\) (2)
Ta có:
\(x_1^2+12=2x_2-x_1.x_2\)
\(\Leftrightarrow x_1^2+12=(x_1+x_2)x_2-x_1.x_2\) (thay \(2 = x_1+ x_2 \))
\(\Leftrightarrow x_1^2- x_2^2 = -12\)
\(\Leftrightarrow (x_1- x_2) (x_1+ x_2)= -12\)
\(\Leftrightarrow x_1- x_2 = - 6\)
Kết hợp với (2) ta có \(\left\{ \matrix{ x_1 = -2\hfill \cr x_2 = 4 \hfill \cr} \right.\)
\(\Rightarrow x_1 x_2 =m-3 = -2.4 = -8\) \(\Rightarrow m = -5\).
KL......
Câu 5:
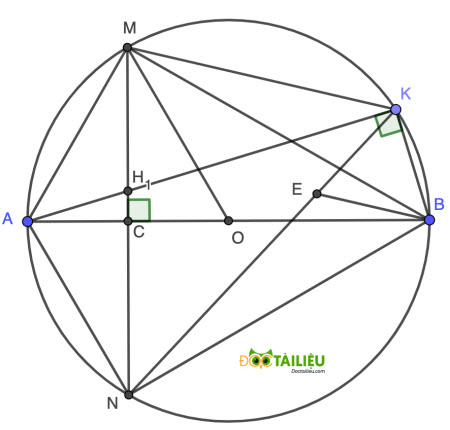
a)
Vì AB là đường kính của (O), K thuộc (O) ⇒ ∠HKB = 90° = ∠HCB ⇒ C, K cùng thuộc đường tròn đường kính HB hay tứ giác BCHK nội tiếp (đpcm).
b)
Vì dây cung MN vuông góc với OA ⇒ A là điểm chính giữa cung MN ⇒ ∠AKM = ∠AMN (cùng \(= \dfrac{1}2 \stackrel\frown{AM}\))
Xét △AMH và △AKM ta có:
Góc HAM chung
∠AKM = ∠AMH (cmt)
Suy ra △AMH ∽ △AKM ⇒ \(\dfrac{AM}{AH} = \dfrac{AK}{AM}\) ⇒ AH.AK = AM² (đpcm).
c)*
Lấy điểm E trên KN sao cho KE = KB (như hình vẽ).
Xét △MAO cân tại O có MC vừa là đường cao, C là trung điểm OA (gt) ⇒ △MAO đều ⇒ ∠MAB = 60° = 180° - ∠MKB ⇒ ∠MKB = 120°.
Lại có \(∠MKN = \dfrac{1}2 ∠MON = \dfrac{1}2 (60° + 60°) = 60°\)
⇒ ∠EKB = ∠MKB - ∠MKN = 60°.
Tam giác KEB có KE = KB, ∠EKB = 60° ⇒ △KEB đều ⇒ KB = KE = BE và ∠KEB = 60°
⇒ ∠NEB = 180° - ∠KEB = 120°.
Xét △BMN, có BC vừa là đường cao vừa là trung tuyến ⇒ △BMN cân tại B ⇒
Xét △MKB và △NEB ta có:
∠BMK = ∠BNE (góc nội tiếp cùng chắn cung KB)
∠MKB = ∠NEB (= 120°) ⇒ ∠KBM = ∠EBN
KB = BE (cmt)
Suy ra △MKB = △NEB ⇒ KM = NE ⇒ KM + KB = NE + KE = KN.
⇒ KM + KN + KB = 2KN.
Vì KN là 1 dây cung của (O;R) ⇒ \(KN \leq 2R\) hay \(KM + KN + KB \leq 4R\).
Vậy \({Max}_{KM + KN + KB} = 4R \Leftrightarrow KN = 2R\) hay KN là đường kính của (O) hay K là điểm chính giữa cung nhỏ MB.
-/-
Trên đây là hướng dẫn giải chi tiết đề thi thử vào 10 môn toán năm 2020 huyện Mê Linh, mong rằng đây sẽ là tài liệu hữu ích giúp các em ôn tập. Đừng quên còn rất nhiều tài liêu đề thi thử vào 10 môn toán khác của các tỉnh thành trên cả nước nhé.
