Cùng Đọc tài liệu thử sức với đề thi thử vào lớp 10 môn toán năm 2020 có đáp án của huyện Thạch Thất vừa diễn ra em nhé:
Đề thi thử
Bài I (2,0 điểm)
Cho hai biểu thức: \(P = \dfrac{x}{\sqrt x -1}\) và \(Q=\dfrac{x-1}{\sqrt x -1} - \dfrac{x\sqrt x +1}{x -1}\)
Với \(x\geq 0; x ≠1\)
1) Tính giá trị của biểu thức P khi x = 4.
2) Rút gọn biểu thức A =Q:P với \(x\geq 0; x ≠1\).
3) Tìm các giá trị x để \(A<-1\).
Bài II (2,0 điểm) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Quãng đường AB dài 60 km. Một người đi xe đạp từ A đến B với vận tốc và thời gian dự định. Sau khi đi được nửa quãng đường người đó giảm vận tốc 5 km/h trên nửa quãng đường còn lại. Vì vậy, người đó đã đến B chậm hơn dự định 1 giờ. Tính vận tốc và thời gian dự định của người đó.
Bài III (2,0 điểm)
1) Giải hệ phương trình:
\(\left\{ \matrix{ \dfrac{1}{x+2} + \dfrac{2}{y+3} = \dfrac{2}{3} \hfill \cr \dfrac{-3}{x+2} + \dfrac{5}{y+3} = \dfrac{3}{4} \hfill \cr} \right.\)
2) Cho phương trình: \(x^2 - (2m+1)x + m^2 - m = 0 \)(1)
a) Giải phương trình (1) với m = 3.
b) Tìm các giá trị của m để phương trình (1) có hai nghiệm phân biệt x1, x2 thỏa mãn điều kiện \(|x_1-x_2|=2\).
Bài IV (3,5 điểm)
Cho đường tròn tâm O có dây AB cố định. Gọi K là điểm chính giữa của cung nhỏ AB. Kẻ đường kính IK cắt AB tại N. Lấy điểm M bất kỳ trên cung lớn AB, MK cắt AB tại D, hai đường thẳng IM và AB cắt nhau tại C.
1) Chứng minh: tứ giác MNKC là tứ giác nội tiếp.
2) Chứng minh: IM.IC = IN.IK
3) Gọi E là giao điểm của hai đường thẳng ID và CK. Chứng minh điểm E thuộc đường tròn tâm O và NC là tia phân giác của góc MNE.
4) Tìm vị trí của điểm M trên cung lớn AB sao cho tích DM.DK đạt giá trị lớn nhất.
Bài V (0,5 điểm)
Cho các số thực x, y, z dương thỏa mãn x+y+z= 1. Tìm giá trị lớn nhất của biểu thức:
\(M = \dfrac{x}{\sqrt{x+yz}} + \dfrac{y}{\sqrt{y+zx}} + \dfrac{z}{\sqrt{z+xy}}\)
Hết
Trên đây là 5 câu hỏi trong đề thi thử lớp 10 của huyện Thạch Thất (Hà Nội) với môn Toán, cùng làm bài thi này trong 120 phút rồi đối chiếu với đáp án chi tiết dưới đây em nhé:
Đáp án
Bài I (2,0 điểm)
1)
Thay x = 4 vào ta có:
\(P = \dfrac{x}{\sqrt x -1}\) \(= \dfrac{4}{\sqrt 4 -1} = 4\)
2)
Với \(x\geq 0; x ≠1\), ta có:
\(A=Q:P =\left(\dfrac{x-1}{\sqrt x -1} - \dfrac{x\sqrt x +1}{x -1}\right) : \dfrac{x}{\sqrt x -1}\)
\( =\left(\dfrac{x-1}{\sqrt x -1} - \dfrac{(\sqrt x +1)(x-\sqrt x+1)}{(\sqrt x -1)(\sqrt x+1)}\right) .\dfrac{\sqrt x -1}{x}\)
\( =\dfrac{x-1- (x-\sqrt x+1)}{\sqrt x -1}.\dfrac{\sqrt x -1}{x}\)
\( =\dfrac{\sqrt x -2}{x}\)
Để A xác định \(\Rightarrow x > 0\) \(\Rightarrow x > 0; x ≠1\).
3)
Với \(x> 0; x ≠1\) để \(A<-1\)
\(\Leftrightarrow \dfrac{\sqrt x -2}{x} < -1\)
\(\Leftrightarrow {x+\sqrt x -2} <0\)
\(\Leftrightarrow (\sqrt x +2)(\sqrt x -1) <0\)
\(\Leftrightarrow \sqrt x <1\)
Kết hợp với đkxđ thì để \(A<-1\) \(\Leftrightarrow 0<>.
Bài II (2,0 điểm)
Gọi vận tốc dự định của người đó là X (km/h - \(X>0\))
Thời gian dự định là: \(\dfrac{60}{X}\) (h)
Theo giả thiết ta có:
\(\dfrac{30}{X} + \dfrac{30}{X-5} =\dfrac{60}{X}+1\)
\(\Leftrightarrow X^2 - 5X - 150 = 0\)
\(\Leftrightarrow (X-15)(X+10) = 0\)
\(\Leftrightarrow X = 15\) (km/h - do \(X>0\))
Kết luận:
Vậy vận tốc dự định của người đó là 15 km/h
Thời gian dự định là \(\dfrac{60}{X} = 4\) giờ.
Bài III (2,0 điểm)
1)
\(\left\{ \matrix{ \dfrac{1}{x+2} + \dfrac{2}{y+3} = \dfrac{2}{3} \hfill \cr \dfrac{-3}{x+2} + \dfrac{5}{y+3} = \dfrac{3}{4} \hfill \cr} \right.\)
ĐKXĐ: \(x ≠ -2; y ≠-3\)
\(\Leftrightarrow \left\{ \matrix{ \dfrac{1}{x+2} = \dfrac{1}{6} \hfill \cr \dfrac{1}{y+3} = \dfrac{1}{4} \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ x = 4 \hfill \cr y = 1 \hfill \cr} \right.\) (thoả mãn đkxđ)
Kết luận ....
2) Cho phương trình: \(x^2 - (2m+1)x + m^2 - m = 0 \) (1)
a)
Với m = 3, thay vào (1) ta có:
\(x^2 - (2.3+1)x + 3^2 - 3 = 0 \)
\(\Leftrightarrow x^2 - 7x + 6 = 0 \)
\(\Leftrightarrow \left[ \matrix{ x=1 \hfill \cr x=6 \hfill \cr} \right.\)
b)
Để phương trình (1) có hai nghiệm phân biệt khi và chỉ khi:
\(\Delta = (2m+1)^2 - 4(m^2-m) = 8m +1 >0\)
\(\Leftrightarrow m > \dfrac{-1}{8}\)
Áp dụng hệ thức Vi-ét cho phương trình (1), ta có:
\( \left\{ \matrix{ x_1+x_2 = 2m+1 \hfill \cr x_1x_2 = m^2 - m \hfill \cr} \right.\)
Ta có:
\(|x_1-x_2|=2\) \(\Leftrightarrow (x_1-x_2)^2=4\)
\(\Leftrightarrow (x_1+x_2)^2 - 4x_1x_2=4\)
\(\Leftrightarrow (2m+1)^2 - 4(m^2-m)=4\)
\(\Leftrightarrow 8m = 3 \Leftrightarrow m = \dfrac{3}8\)
(thoả mãn đk)Kết luận...
Bài IV (3,5 điểm)
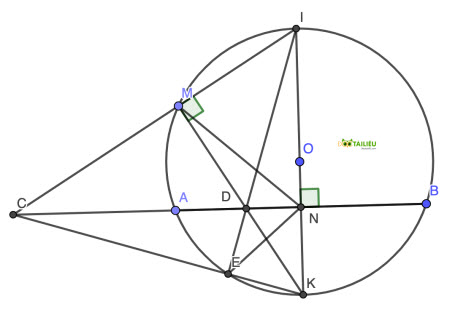
1)
Điểm M chắn cung IK là đường kính của (O) nên ∠KMI = 90° hay ∠KMC = 90°.
K là điểm chính giữa cung AB nên OK ⊥ AB hay ∠KNC = 90°.
Suy ra N và M cùng thuộc đường tròn đường kính KC, hay tứ giác MNKC nội tiếp (đpcm).
2)
Vì tứ giác MNKC nội tiếp ⇒ ∠NKC = 180° - ∠CMN = ∠NMI.
Xét △IMN và △IKC, có:
Góc MIN chung
∠NKC = ∠NMI (cmt)
Suy ra △IMN ∽ △IKC ⇒ \(\dfrac{IM}{IN} = \dfrac{IK}{IC} \) ⇒ IM.IC = IN.IK (đpcm).
3)
Xét △IKC có KM ⊥ IC, CN ⊥ IK và D là giao điểm của hai đường cao ⇒ D là trực tâm của △IKC ⇒ ID ⊥ KC hay ∠IEK = 90°
Suy ra E thuộc đường tròn đường kính IK hay E thuộc đường tròn (O) (đpcm).
Vì ∠DEK = ∠DNK = 90° ⇒ Tứ giác DEKN nội tiếp ⇒ ∠DNE = ∠DKE = 90° - ∠EDK = 90° - ∠MDI = ∠MID (1)
Tương tự Vì ∠DMI = ∠DNI = 90° ⇒ Tứ giác DNIM nội tiếp ⇒ ∠DNM = ∠MID (2)
Từ (1) và (2) suy ra ∠DNE = ∠DNM ⇒ NC là tia phân giác của góc MNE (đpcm).
4)
Xét △DMA và △DBK, có:
∠MDA = ∠BDK (đối đỉnh)
∠AMD = ∠KBD (góc nội tiếp cùng chắn cung AK)
Suy ra △DMA ∽ △DBK ⇒ \(\dfrac{DM}{DA} = \dfrac{DB}{DK} \) ⇒ DM.DK = DA.DB
Áp dụng BĐT AM-GM ta có:
\(DA.DB \leq \dfrac{1}{4} (DA+DB)^2 = \dfrac{1}{4} {AB}^2\)
\(\Leftrightarrow DM.DK \leq \dfrac{1}{4} {AB}^2\)
Vậy để DM.DK đạt giá trị lớn nhất \(\Leftrightarrow DM.DK =\dfrac{1}{4} {AB}^2\) \(\Leftrightarrow DA = DB\) hay D là trung điểm của AB, hay M là điểm chính giữa cung lớn AB.
Bài V (0,5 điểm)
Ta có:
\( \dfrac{x}{\sqrt{x+yz}} = \dfrac{x}{\sqrt{x(x+y+z)+yz}} = \dfrac{x}{\sqrt{(x+y)(x+z)}} \)
Áp dụng BĐT AM-GM cho \(\dfrac{x}{{x+y}}\) và \(\dfrac{ x}{{x+z}}\), ta có:
\(\dfrac{1}{{2}} \left(\dfrac{x}{{x+y}} + \dfrac{ x}{{x+z}} \right) \geq \dfrac{x}{\sqrt{(x+y)(x+z)}} = \dfrac{x}{\sqrt{x+yz}} \)
Tương tự ta có:
\(\dfrac{1}{{2}} \left(\dfrac{y}{{y+x}} + \dfrac{ y}{{y+z}} \right) \geq \dfrac{y}{\sqrt{y+zx}} \)
\(\dfrac{1}{{2}} \left(\dfrac{z}{{z+x}} + \dfrac{z}{{z+y}} \right) \geq \dfrac{z}{\sqrt{z+xy}} \)
Cộng vế theo vế 3 bất đẳng thức trên, ta có:
\(M = \dfrac{x}{\sqrt{x+yz}} + \dfrac{y}{\sqrt{y+zx}} + \dfrac{z}{\sqrt{z+xy}} \leq \) \(\dfrac{1}{{2}} \left(\dfrac{x}{{x+y}} + \dfrac{ x}{{x+z}} \right) + \dfrac{1}{{2}} \left(\dfrac{y}{{y+x}} + \dfrac{ y}{{y+z}} \right) + \dfrac{1}{{2}} \left(\dfrac{z}{{z+x}} + \dfrac{ z}{{z+y}} \right) \)
\(\Leftrightarrow M \leq \dfrac{3}{2}\)
Vậy \({Max}_M = \dfrac{3}{2} \Leftrightarrow x=y=z = \dfrac{1}{3}\).
-/-
Trên đây là hướng dẫn giải chi tiết đề thi thử vào 10 môn toán năm 2020 huyện Thạch Thất, mong rằng đây sẽ là tài liệu hữu ích giúp các em ôn tập. Đừng quên còn rất nhiều tài liêu đề thi thử vào 10 môn toán khác của các tỉnh thành trên cả nước nhé.
