Cùng Đọc tài liệu thử sức với đề thi thử tuyển sinh vào lớp 10 môn toán năm 2020 có đáp án của GD&ĐT tỉnh Vĩnh Phúc vừa diễn ra ngày 24/6/2020 em nhé:
Đề thi thử
|
SỞ GD&ĐT THÀNH PHỐ CẦN THƠ ĐỀ CHÍNH THỨC |
KIỂM TRA HỌC KỲ II LỚP 9 NĂM HỌC 2019 - 2020 MÔN TOÁN Thời gian làm bài: 90 phút (Không kể thời gian giao đề) |
Đề kiểm tra gồm hai phần: Trắc nghiệm và Tự luận.
A. PHẦN TRẮC NGHIỆM (4,0 điểm; gồm 20 câu, từ câu 1 đến câu 20, mỗi câu 0,2 điểm).
Câu 1. Tập nghiệm của phương trình x² - 5x + 6 = 0 là
A. {1;6}.
B. {2;3}.
C. {-6; -1}.
D. {-3;2}.
Câu 2. Cho đường tròn (O) có hai dây AB và CD cắt nhau tại E (như hình vẽ bên dưới). Biết sđ \(\stackrel\frown{AmC} = 80°\) và sđ \(\stackrel\frown{BnD} = 30°\). Số đo góc ∠AEC bằng
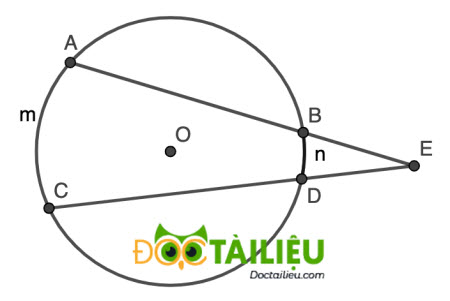
A. 30°
B. 55°
C. 25°
D. 50°
Câu 3. Gọi \(x_1, x_2 \)là nghiệm của phương trình 3x² - ax + b=0, Tổng \(x_1 + x_2\) bằng
A. \(\dfrac{a}{3}\)
B.\(-\dfrac{a}{3}\)
C.\(-\dfrac{b}{3}\)
D. \(\dfrac{b}{3}\)
Câu 4. Cho các điểm A, B, C nằm trên đường tròn (O) sao cho ∠OBC = 44° (như hình vẽ bên dưới). Số đo của góc ∠BAC bằng
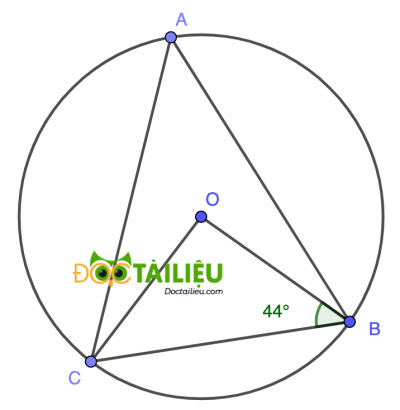
A. 66°
B. 36°
C. 56°
D. 46°.
Câu 5. Trong các điểm sau đây, điểm nào thuộc đồ thị của hàm số \(y = -\dfrac{1}{2}x^2\)
A. \(\left(1;\dfrac{1}{2}\right)\)
B. \(\left(-\dfrac{1}{2}; 1\right)\)
C. \(\left(1;-\dfrac{1}{2}\right)\)
D. \(\left(\dfrac{1}{2};1\right)\)
Câu 6. Tất cả giá trị của tham số m sao cho phương hinh \(x²-2mx+m²-m+1=0\) có nghiệm là
A. m ≤ -1.
B. m ≥ 1.
C.m ≥ -1.
D. m ≤ 1.
Câu 7. Phương trình nào sau đây không phải là phương trình bậc hai một ẩn ?
A. x³ - 5x - 9=0.
B. -x² = 0.
C. 3x² - 2x = 0.
D. x² +2 = 0.
Câu 8. Gọi \(x_1,x_2\), là nghiệm của phương trình x² - 8x + 10 = 0. Giá trị của \(\dfrac{1}{x_1} + \dfrac{1}{x_2}\) bằng
A. \(\dfrac{-5}{4}\)
B. \(\dfrac{5}{4}\)
C. \(\dfrac{-4}{5}\)
D. \(\dfrac{4}{5}\)
Câu 9. Phương trình 2x² – 4x + 1 = 0 có biệt thức △ bằng
A.-4.
B. 2.
C. 8.
D. 24.
Câu 10. Cho hàm số y=ax² có đồ thị như hình vẽ bên dưới.
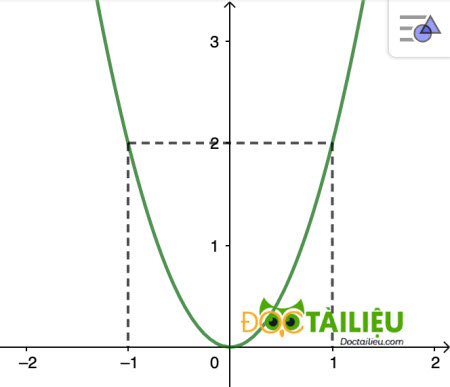
Hàm số đó là
A. y = 2x²
B. y = x²
C. y = -x²
D. y = -2x²
Câu 11. Cho đường tròn (O) có hai dây AB và CD cắt nhau tại I. Gọi F là điểm thuộc đường tròn sao cho ∠BFC=47° và ∠AFD=52° (như hình với). Số đo của góc ∠AID bằng
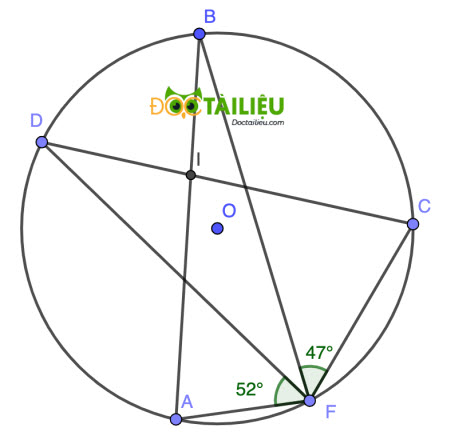
A. 96°
B. 99°
C. 98°
D. 97°
Câu 12. Phương trình (m+2)x² - 2mx + 1 = 0 không phải là phương trình bậc hai một ẩn khi m bằng
A. 0.
B. 2.
C. -2.
D. 1.
Câu 13. Giá trị của tham số m sao cho phương trình x² - x + m= 0 có một nghiệm x = 2 là
A. -2.
B. 0.
C. 2.
D. 6.
Câu 14. Nếu hai số \(x_1, x_2\) thỏa mãn \( x_1 +x_2 = S\) và \(x_1.x_2= P\) thì \(x_1, x_2\) là nghiệm của phương trình nào sau đây?
A. x² - Sx - P = 0.
B. x² + Sx + P = 0.
C. x² + Sx - P = 0.
D. x² - Sx + P = 0.
Câu 15. Gọi S và P là tổng và tích hại nghiệm của phương trình x² – 7x+12 = 0. Khi đó giá trị của S+P bằng
A. 5.
B.-5.
C. 19.
D.-19.
Câu 16. Cho hàm số \( y= \dfrac{1}{4}x^2\). Khẳng định nào sau đây đúng?
A. Hàm số trên luôn nghịch biến.
B. Hàm số trên đồng biến khi \(x > 0\), nghịch biến khi \(x < 0\).
C. Hàm số trên đồng biến khi \(x < 0\), nghịch biến khi \(x > 0\).
D. Hàm số trên luôn đồng biến.
Câu 17, Cho hai điểm A, B nằm trên đường tròn (O;R) sao cho sđ \(\stackrel\frown{AB}=120°\)
, Diện tích hình quạt OAB bằngA.\(\dfrac{πR^2}{3}\)
B. \(\dfrac{πR^2}{2}\)
C. \(\dfrac{πR^2}{4}\)
D. \(\dfrac{πR^2}{6}\)
Câu 18. Trong một đường tròn, xét các khẳng định sau:
(I). Số đo của góc có đỉnh ở bên trong đường tròn bằng tổng số đo hai cũng bị chắn.
(II). Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
(III). Số đo của góc nội tiếp bằng số đo của cung bị chắn. (IV), Số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn. Số khẳng định đúng là
A. 4.
B.1.
C. 3.
D. 2.
Câu 19. Điểm A(-1;2) thuộc đồ thị hàm số nào dưới đây?
A. \(y = \dfrac{1}{2}x^2\).
B. \(y = -2x^2\).
C. \(y = - \dfrac{1}{2}x^2 \)
D. \(y=2x^2\).
Câu 20. Số nghiệm của phương trình x⁴ – 6x² + 9=0 là
A. 0.
B. 2.
C. 1.
D. 4.
B. PHẦN TỰ LUẬN (6,0 điểm; gồm 4 câu, từ câu 1 đến câu 4).
Câu 1. (1,5 điểm) Giải hệ phương trình và phương trình sau:
a) \(\left\{ \matrix{ x - y = 1 \hfill \cr 2x + y = 5 \hfill \cr} \right.\)
b) 4x⁴ + x² - 5=0
Câu 2. (1,0 điểm) Cho phương trình x²-(2m+1)x + m²-1=0 (*) (m là tham số).
a) Giải phương trình (*) khi m=1..
b) Tìm các giá trị của m sao cho phương trình (*) có hai nghiệm phân biệt \(x_1, x_2\), thỏa mãn \(x_1x_2 -2(x_1 + x_2)=9\).
Câu 3. (1,0 điểm) Một khu vườn dạng hình chữ nhật có diện tích bằng 600m² và chiều dài hơn chiều rộng là 10m. Tính chu vi của khu vườn.
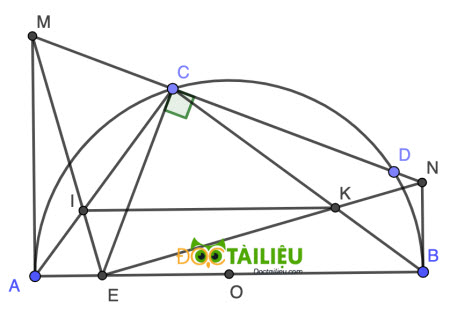
Câu 4. (2,5 điểm) Cho nửa đường tròn đường kính AB và một dây CD (CD không song song với AB và D thuộc cung BC). Qua C vẽ đường thẳng vuông góc với CD, cắt AB tại E. Các tiếp tuyến tại A và B của nửa đường tròn cắt đường thẳng CD theo thứ tự tại M và N.
a) Chứng minh các tứ giác AMCE và BNCE nội tiếp.
b) Chứng minh tam giác ACB đồng dạng với tam giác MEN.
c) Gọi I là giao điểm của AC và ME, K là giao điểm của BC và E. Chứng minh đường thẳng IK song song với đường thẳng AB.
Hết
Đáp án
A. PHẦN TRẮC NGHIỆM (4,0 điểm; gồm 20 câu, từ câu 1 đến câu 20, mỗi câu 0,2 điểm).
| 1B | 2C | 3A | 4D | 5C |
| 6B | 7A | 8D | 9C | 10A |
| 11B | 12C | 13A | 14D | 15C |
| 16B | 17A | 18D | 19D | 20B |
B. PHẦN TỰ LUẬN (6,0 điểm; gồm 4 câu, từ câu 1 đến câu 4).
Câu 1.
a) \(\left\{ \matrix{ x - y = 1 \hfill \cr 2x + y = 5 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ x = 2 \hfill \cr y=1 \hfill \cr} \right.\)
b) 4x⁴ + x² - 5=0
\(\Leftrightarrow \left[ \matrix{ x^2 = 1 \hfill \cr x^2=-\dfrac{5}4 \space (loại) \hfill \cr} \right.\)
\(\Rightarrow \left[ \matrix{ x = 1 \hfill \cr x = -1 \hfill \cr} \right.\)
Câu 2.
a)
Thay m = 1, ta có:
(*) \(\Leftrightarrow x^2-(2+1)x + 1-1=0\)
\(\Leftrightarrow x^2-3x =0\)
\(\Rightarrow \left[ \matrix{ x = 0 \hfill \cr x = 3 \hfill \cr} \right.\)
b)
Để phương trình (*) có hai nghiệm phân biệt:
\(\Delta = (2m+1)^2 - 4(m^2-1) > 0 \Leftrightarrow 4m + 5 > 0 \Leftrightarrow m > -\dfrac{5}4\)
Áp dụng hệ thức Vi-ét cho (*), ta có:
\(\left\{ \matrix{ x_1+x_2 = 2m+1 \hfill \cr x_1x_2 = m^2-1 \hfill \cr} \right.\)
Ta có:
\(x_1x_2 -2(x_1 + x_2)=9 \Leftrightarrow (m^2-1) - 2(2m+1) = 9\)
\( \Leftrightarrow m^2- 4m - 12 = 0\)
\(\Leftrightarrow \left[ \matrix{ m = 6 \space (tm \space đk) \hfill \cr m =-2 \space (loại) \hfill \cr} \right.\)
Câu 3.
Gọi chiều rộng của khu vườn là A (mét, A > 0)
Ta có:
\(S = A.(A+10) = 600\) (m²)
\(\Leftrightarrow \left[ \matrix{ A = 20 \space (tm \space đk) \hfill \cr A =-30 \space (loại) \hfill \cr} \right.\)
Suy ra chu vi của khu vườn là:
\(P = 2.(A+A+10) = 100\) (m).
KL.....
Câu 4.
a)
Vì MA và NB là tiếp tuyến tại A và B ⇒ ∠MAE = ∠NBE = 90°.
Từ giả thiết CE ⊥ CD ⇒ ∠DCE = 90°.
Xét tứ giác AMCE có ∠MAE = ∠MCE = 90° ⇒ A và C cùng thuộc đường tròn đường kính ME hay tứ giác AMCE nội tiếp (đpcm).
Tương tự, có ∠NBE = ∠NCE = 90° ⇒ B và C cùng thuộc đường tròn đường kính NE hay tứ giác BNCE nội tiếp (đpcm).
b)
Vì tứ giác AMCE nội tiếp ⇒ ∠CAE = ∠CME (góc nội tiếp cùng chắn cung CE) hay ∠CAB = ∠EMN.
Tương tự, vì tứ giác BNCE nội tiếp ⇒ ∠CNE = ∠CBE (góc nội tiếp cùng chắn cung CE) hay ∠CBA = ∠ENM.
Xét △ACB và △MEN, ta có:
∠CAB = ∠EMN (cmt)
∠CBA = ∠ENM (cmt)
Suy ra △ACB ∽ △MEN (đpcm).
c)
Vì C thuộc nửa đường tròn đường kính AB ⇒ ∠ACB = 90°
Vì △ACB ∽ △MEN (cmt) ⇒ ∠ACB = ∠MEN = 90° ⇒ C và E cùng thuộc đường tròn đường kính IK, hay tứ giác ICKE nội tiếp.
⇒ ∠CIK = ∠CEK = 90° - ∠MEC = ∠EMC = ∠EAC
Mà 2 góc ∠CIK và ∠EAC nằm tại vị trí đồng vị với nhau ⇒ IK // AB (đpcm).
-/-
Trên đây là hướng dẫn giải chi tiết đề thi khảo sát học kì 2 môn Toán 9 năm 2019/2020 của TP. Cần Thơ, mong rằng đây sẽ là tài liệu hữu ích giúp các em ôn tập. Đừng quên còn rất nhiều tài liêu đề thi thử vào 10 môn toán khác của các tỉnh thành trên cả nước nhé.
