Cùng Đọc Tài Liệu tham khảo đáp án đề thi HSG Toán 9 thành phố Hà Nội năm 2020 - 2021 dưới đây bạn nhé:
Đề thi HSG Toán 9 thành phố Hà Nội năm 2020
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KỲ THI CHỌN HỌC SINH GIỎI LỚP 9 CẤP THÀNH PHỐ
Năm học 2020 - 2021
Môn thi: TOÁN
Ngày thi: 13/1/2021
Thời gian làm bài: 150 phút
Bài I (5,0 điểm)
1) Giải phương trình \(x^{2}-x+8=4 \sqrt{x+3}\)
2) Cho a, b, c là các số thực đôi một khác nhau. Chứng minh biểu thức
\(K=\dfrac{a^{2}}{(a-b)(a-c)}+\dfrac{b^{2}}{(b-a)(b-c)}+\dfrac{c^{2}}{(c-a)(c-b)}\) có giá trị nguyên.
Bài II ( 5,0 điểm)
1) Biết a, b, c là các số nguyên thỏa mãn a + b + c chia hết cho 3 và ab - bc - ca chia hết cho 3 . Chứng minh ab - bc - ca chia hết cho 9 .
2) Cho đa thức \(P(x)=x^{3}+a x+b\) có nghiệm \(1+\sqrt{3}\) (a, b là các số hữu tỉ). Chứng minh P(x) chia hết cho đa thức \(x^{2}-2 x-2\)
Bài III (2,0 điểm) Với các số thực không âm a, b, c thỏa mãn \(a^{2}+b^{2}+c^{2}=1\), tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức \(Q=\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a}\).
Bài IV (6,0 điểm) Cho đường tròn (I) nội tiếp tam giác nhọn \(ABC (A B < A C)\). Đường tròn (I) tiếp xúc với BC, CA lần lượt tại D, E. Qua B kẻ đường thẳng vuông góc với BI, cắt AI tại J. Gọi P là hình chiếu vuông góc của J trên BC.
1) Chứng minh BD = CP.
2) Gọi N là giao điểm củaa hai đường thẳng AJ và BC. Chứng minh \(\dfrac{1}{A I}+\dfrac{1}{A J}=\dfrac{2}{A N}\).
3) Gọi Q là giao điểm của hai đường thằng JP và DE. Gọi K là trung điểm của PQ. Chứng minh BK vuông góc với AP.
Bài V (2,0 điềm)
1) Tìm tất cả các số nguyên dương x, y, z thỏa mãn \(3^{x}+2^{y}=1+2^{z}\).
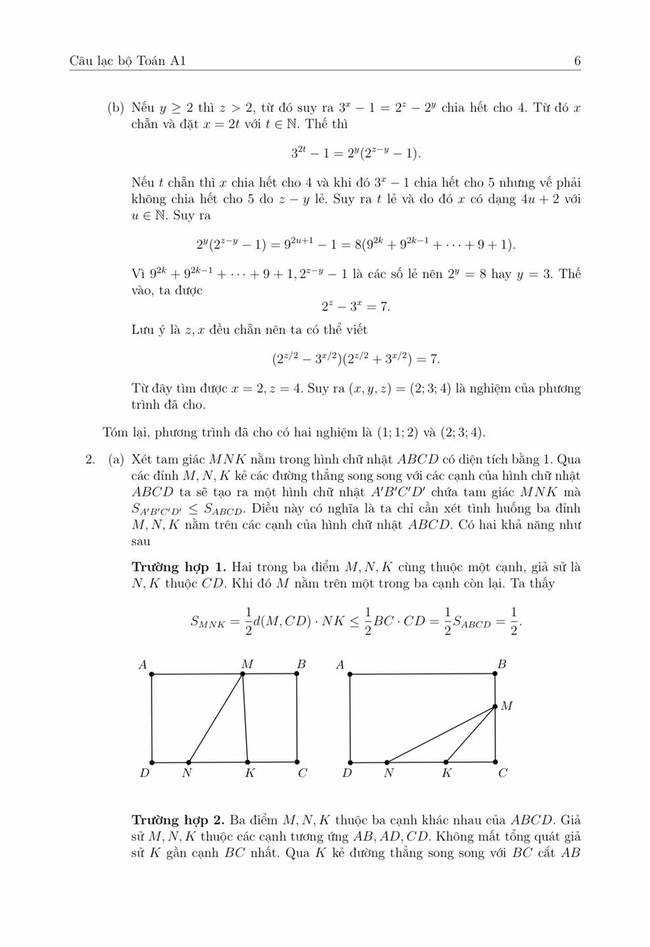
2) Cho một hình chữ nhật có diện tích bằng 1. Năm điểm phân biệt được đặt tùy ý vào hình chữ nhật sao cho không có ba điểm nào thằng hàng (mỗi điểm trong năm điểm đó có thể được đặt trên cạnh hoặc đặt nằm trong hình chữ nhật).
a) Chứng minh mọi tam giác tạo bởi ba trong năm điểm đã cho đều có diện tích không vượt quá \(\dfrac{1}{2}\)
b) Với mỗi cách đặt năm điểm vào hình chữ nhật như trên, gọi N là số tam giác có ba đỉnh là ba điểm trong năm điểm đó và có diện tích không vượt quá \(\dfrac{1}{4}\). Tìm giá trị nhỏ nhất của N.
Đáp án đề thi HSG Toán 9 thành phố Hà Nội năm 2020 - 2021
Bài I
1. Điều kiện xác định: \(x \geq-3\). Phương trình ban đầu tương đương với
\((x-1)^{2}+(\sqrt{x+3}-2)^{2}=0 \Longleftrightarrow x-1=\sqrt{x+3}-2=0 \Longleftrightarrow x=1\)
Vậy S= 1
2. Quy đồng mẫu số biểu thức K thì ta được
\(K=\frac{a^{2}(c-b)+b^{2}(a-c)+c^{2}(b-a)}{(a-b)(b-c)(c-a)}\)
Phân tích thành nhân tử ở tử số của K
Tỷ số
\(K =a^{2}(c-a+a-b)+b^{2}(a-c)+c^{2}(b-a) \\ =(c-a)\left(a^{2}-b^{2}\right)+(a-b)\left(a^{2}-c^{2}\right) \\ =(c-a)(a-b)(a+b)+(a-b)(a-c)(a+c) \\ =(a-b)(c-a)(a+b-a-c) \\ =(a-b)(b-c)(c-a)\)
Do vây, K=1 \(\in \mathbb{Z}\).
Bài II
1. Đặt a+b+c=3k (với \(k \in \mathbb{Z}\) ). Khi đó ta có \(c=3 k-(a+b)\)
Vì vậy
\(a b-b c-c a =a b-c(a+b) \\ =a b-3 k(a+b)+(a+b)^{2} \\ =a^{2}+b^{2}+3 a b-3 k(a+b) .\)
Từ giả thiết ta suy ra \(a^{2}+b^{2}\) chia hết cho 3 . Sử dụng kết quả quen thuộc ta suy ra a, b đều chia hết cho 3 , điều này cũng kéo theo c chia hết cho 3 .
Như vậy, ab - bc - ca chia hết cho 9
2. Ta có \(P(1+\sqrt{3})=0\) nên \((1+\sqrt{3})^{3}+a(1 \sqrt{3})+b=0\) hay
\((a+b+10)+(a+6) \sqrt{3}\)
=0Vì a, b là các số hữu tỉ nên a + b + 10, a + 6 cũng là các số hữu tỉ nên theo kết quả suy ra \(a+b+10=a+6=0\) . Khi đó \(P(1-\sqrt{3})=(a+b+10)-(a+6) \sqrt{3}= 0\).
Điều này có nghĩa là P(x) có nghiệm là \(1-\sqrt{3}\). Suy ra P(x) chia hết cho \((x-(1+\sqrt{3}))(x-(1-\sqrt{3}))=x^{2}-2 x-2\)
Bài III
1. Vì \((a+b+c)^{2} \leq 3\left(a^{2}+b^{2}+c^{2}\right)=3\) nên \(a+b+c \leq \sqrt{3}\). Áp dụng bất đẳng thức Bunhiacovsky, ta có
\(Q^{2} \leq 3(a+b+b+c+c+a)=6(a+b+c) \leq \sqrt{108}\)
nên \(Q \leq \sqrt[4]{108}\). Dấu bằng xảy ra khi và chỉ khi \(a=b=c=\frac{1}{\sqrt{3}}\). Từ đó giá trị lớn nhất của Q là \(\sqrt[4]{108}\).
2. Từ giả thiết suy ra \(a, b, c \leq 1\) kéo theo \(a \geq a^{2}, b \geq b^{2}, c \geq c^{2}\) .
Ta có
\(Q^{2}=2(a+b+c)+2 \sqrt{(a+b)(a+c)}+2 \sqrt{(b+c)(b+a)}+2 \sqrt{(c+a)(c+b)}\)
và lưu ý là \((a+b)(a+c) \geq a^{2}, \ldots\) nên \(Q^{2} \geq 4(a+b+c) \geq 4\left(a^{2}+b^{2}+c^{2}\right)=4\) .
Suy ra \(Q \geq 2\)
Dấu bằng xảy ra chẳng hạn khi a=1, b=c=0. Vây giá trị nhỏ nhất của Q là 2 .
Bài IV
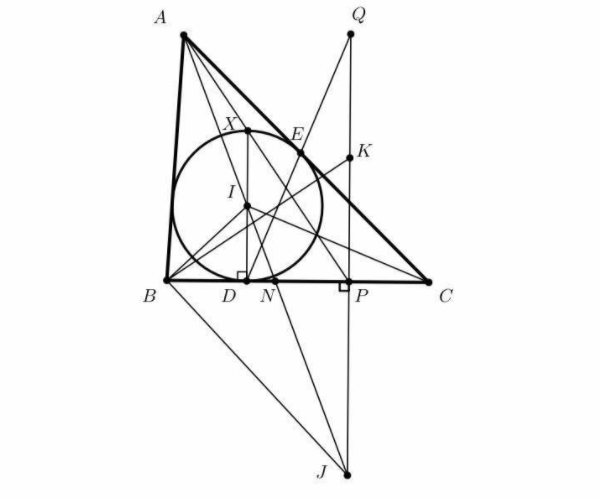
1. Từ giả thiết ta suy ra J là tâm của đường tròn (J) bàng tiếp đỉnh A của tam giác ABC và P là tiếp điểm của đường tròn (J) với cạnh BC . Đặt BC=a, CA= b, AB=c và \(p=\frac{a+b+c}{2}\) . Từ kết quả quen thuộc thì ta có
\(BD = CP = p-b = \frac{A B+B C-C A}{2}\)
2. 2. Ta có BI, BJ tương ứng là phân giác trong và phân giác ngoài của \(\widehat{A B C}\). Sử dụng tính chất phân giác cho tam giác ABN thì ta được
\(\frac{A N}{A I}=\frac{B A+B N}{B A}\) và \(\frac{A N}{A J}=\frac{B A-B N}{B A}\)
Do đó, \(\frac{A N}{A I}+\frac{A N}{A J}=2\) Từ đó suy ra \(\frac{1}{A I}+\frac{1}{A J}=\frac{2}{A N}\)
3. Dựng đường kính DX của đường tròn (I). Ta có kết quả quen thuộc rằng A, X, P thẳng hàng. Chú ý rằng ta có \(C I \perp D E\)
Do \( \widehat{D I C}=\widehat{P D Q}\left(=90^{\circ}-\widehat{I C B}\right) \) nên \(\triangle I D C \sim \triangle D P Q(g.g) .\)
Từ đó suy ra \(\frac{D P}{P Q}=\frac{I D}{C D}=\frac{I D}{B P}\) .
Để ý rằng DX = 2 ID và PQ = 2PK, nên ta được
\(\frac{D P}{P K}=\frac{2 D P}{P Q}=\frac{2 I D}{B P}=\frac{D X}{B P}\)
Điều này kéo theo \(\triangle D P X \sim \triangle P K B(\mathrm{c.g.c})\) .
Do dó, \(\widehat{A P B}=\widehat{X P D}=\widehat{B K P}= 90^{\circ}-\widehat{P B K}\)
hay \(\widehat{A P B}+\widehat{P B K}=90^{\circ}\) .
Vì vậy, \(B K \perp A P\)
Bài V
1. Ta có \(1+2^{z}=3^{x}+2^{y}>2^{y}\) nên \(z>y\). Ngoài ra vì \(2^{y}-2^{z} \equiv 1(\bmod 3)\) nên z chẵn, còn y lẻ.
Xét các khả năng
(a) Nếu y=1 thì \(3^{x}=2^{z}-1=\left(2^{k}-1\right)\left(2^{k}+1\right)\) với \(k=\frac{z}{2}\) .
Vì \(\left(2^{k}+1\right)-\left(2^{k}-1\right)=2\) không chia hết cho 3 nên \(2^{k}-1=1\) kéo theo k=1.
Từ đó tìm được z=2, x=1.
Suy ra (x, y, z)=(1 ; 1 ; 2) là một nghiệm của phương trình đã cho.



"Lời giải đề thi chọn học sinh giỏi lớp 9 môn Toán, thành phố Hà Nội năm học 2020-2021, được thực hiện bởi các thành viên của Tổ Kiến (Câu lạc bộ Toán A1)."
-/-
Trên đây là đề thi HSG Toán 9 thành phố Hà Nội năm 2020 - 2021 do Đọc tài liệu tổng hợp, mong rằng với nội dung này sẽ giúp các em ôn tập kiến thức thi cuối kì 1 tốt hơn. Đừng quên còn trọn bộ đề thi thử vào 10 môn Toán qua các năm đang đợi các em giải đáp.
