Sở GD&ĐT An Giang vừa công bố đề thi minh họa tham khảo tuyển sinh vào lớp 10 năm học 2020/2021 môn Toán như sau:
Đề thi minh họa tham khảo tuyển sinh vào lớp 10 môn Toán 2020 tỉnh An Giang
Bài 1.
(3,0 điểm) Giải các phương trình và hệ phương trình sau đâya. \(\sqrt{7}x + 2\sqrt{7} = 0\);
b. \(\left\{ \matrix{ x + 3y = 7 \hfill \cr -x + 3y = 5 \hfill \cr} \right.\).
c. \(x^4 + 4x^2 – 5 = 0\).
Bài 2. (2,0 điểm) Cho hàm số \(y = -x^2\) có đồ thị là parabol (P).
a. Vẽ đồ thị (P) trên hệ trục tọa độ.
b. Viết phương trình đường thẳng (d) tiếp xúc parabol (P). Biết (d) cắt trục hoành và trục tung tại hai điểm A và B sao cho tam giác OAB vuông cân với 0 là gốc toạ độ.
Bài 3. (1,5 điểm) Cho phương trình bậc hai \(x^2 – mx + m – 1 = 0\) (m là tham số).
a. Cho m = 3. Giải phương trình đã cho với ẩn số là x.
b. Tìm m để phương trình đã cho có nghiệm kép, tìm nghiệm kép đó.
Bài 4. (2,5 điểm)
Cho tam giác ABC có ba góc đều nhọn, vẽ đường tròn tâm (0) đường kính BC cắt hai cạnh AB, AC lần lượt tại D và E. Gọi H là giao điểm của BE và CD.
a. Chứng minh ADHE là tứ giác nội tiếp.
b. Gọi F là giao điểm của AH với BC. Chứng minh rằng DH là tia phân giác của ∠EDF.
Bài 5. (1,0 điểm)
Gấp tờ giấy A4 có kích thước 210mm x 297mm theo đường chéo ta được một hình như hình vẽ bên. Tính diện tích hình sau khi đã xếp (phần tô đậm).
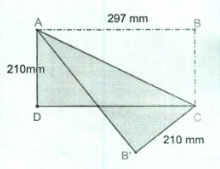
Ngoài nội dung đề thi minh họa tham khảo tuyển sinh vào 10 môn Toán tỉnh An Giang năm 2020, mời các em học sinh tham khảo thêm nội dung đề thi minh họa tuyển sinh vào 10 tỉnh An Giang các môn thi khác dưới đây:
- Đề thi tham khảo tuyển sinh vào 10 Môn Văn tỉnh An Giang năm 2020
- Đề thi minh họa tham khảo tuyển sinh vào 10 môn Anh tỉnh An Giang năm 2020
Đáp án đề tham khảo vào 10 môn Toán tỉnh An Giang
Bài 1.
a. \(x = -2\);
b. \(\left\{ \matrix{ x + 3y = 7 \hfill \cr -x + 3y = 5 \hfill \cr} \right.\) ⇔ \(\left\{ \matrix{ 6y=12 \hfill \cr -x + 3y = 5 \hfill \cr} \right.\)⇔\(\left\{ \matrix{ y=2 \hfill \cr x = 1 \hfill \cr} \right.\)
c. \(x^4 + 4x^2 – 5 = 0\).
Đặt \(t = x^2 (Đ/k: t > 0)\)
=> Ta có phương trình:
\(t^2+4t-5 = 0\)
⇔\((t-1)(t+5)=0\)
⇔\(\left[ \begin{align}& t=1(t/m) \\& t=-5 (loại) \\\end{align} \right.\\\)
Vậy với \(t = 1 => x = ±1\)
KL:...
Bài 2. (2,0 điểm) Cho hàm số \(y = -x^2\) có đồ thị là parabol (P).
a. Vẽ đồ thị (P) \(y = -x^2\)
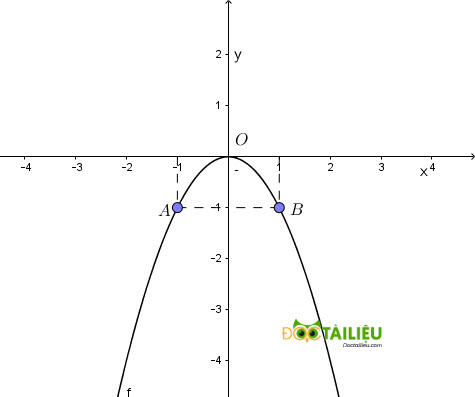
b. Vì phương trình đường thẳng (d) tiếp xúc parabol (P) tại hai điểm A và B => ta gọi phương trình đường thẳng d cần tìm là y = ax + b
Mặt khác tam giác OAB vuông cân tại O là gốc toạ độ
- Góc tạo bởi đường thẳng (d) với trục Ox là 45⁰ hoặc 135⁰ => hệ số góc a = ±1
=> (d): y = ±x + b
Tọa độ giao điểm tiếp xúc của (d) và (P) là nghiệm duy nhất của phương trình \(- x^2 = ±x + b\)
⇔\(x^2 ±x - b =0\) hay △ = 0
TH1: \(x^2 + x - b =0\)
\(△ = -1^2 - 4.(-b).1 = -1+4b=0\) => \(b = \dfrac{1}{4}\)
TH2: \(x^2 - x - b =0\)
\(△ = 1^2 - 4.(-b).1 = 1+4b=0\)=>\(b = \dfrac{-1}{4}\)
KL:...
Bài 3. (1,5 điểm) Cho phương trình bậc hai \(x^2 – mx + m – 1 = 0\) (m là tham số).
a.
m = 3 thì phương trình đã cho thành \(x^2 – 3x + 2 = 0\)
⇔\((x-1)(x-2)=0\)
⇔\(\left[ \begin{align}& x=1 \\& x = 2\\\end{align} \right.\\\)
KL:...
b.
PT: \(x^2 – mx + m – 1 = 0\) có nghiệm kém khi △ = 0
\(△ = m^2 - 4(m-1) = 0\)
⇔ \(m^2 - 4m + 4 = 0\)
⇔ \((m-2)^2 = 0\)
⇔ \(m=2\)
KL:...
Bài 4:
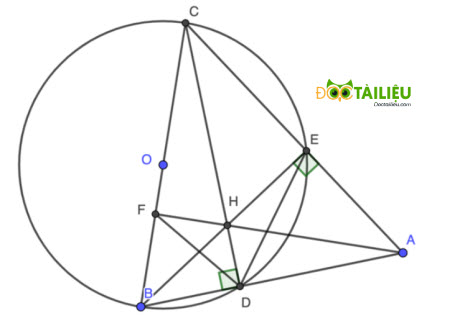
a,
Vì tứ giác CEDB nội tiếp đường tròn (O) đường kính BC nên ta có:
\(\left\{ \matrix{ BE ⊥AC \hfill \cr CD ⊥AB\hfill \cr} \right.\) \(\Rightarrow \angle HEA = \angle HDA = 90 ⁰\) \(\Rightarrow\) tứ giác ADHE nội tiếp (đpcm)
b,
Chứng minh tương tự ý a, ta có các tứ giác HFBD, HFCE, ADHE nội tiếp
\(\Rightarrow\) \(\angle FDH=\angle FBH=\angle CBE \) (1)
và \(\angle EDH=\angle EAH=\angle CAF\) (2)
Lại có: \(\angle CBE = 90 ⁰-\angle BCE = 90 ⁰-\angle FCA = \angle CAF\) (3)
Từ (1) (2) và (3), ta có: \(\angle FDH = \angle EDH\) hay DH là phân giác của góc FDE (đpcm)
Bài 5:
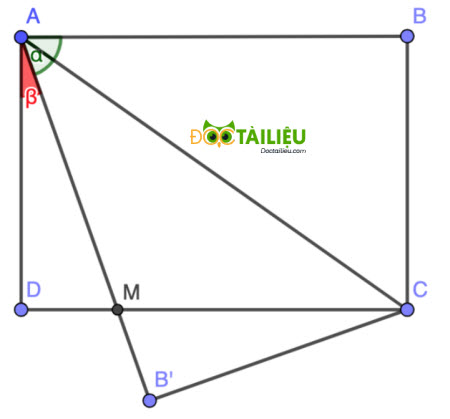
Gọi AB' giao DC tại M.
Gọi \(\angle BAC = \angle CAB' = \alpha\) \(\Rightarrow \angle DAM= \frac{\pi}{2}-2\alpha \)
Ta có: \(S = S_{ADC}+ S_{AB'C}- S_{AMC}\) \(= 2S_{ADC}- S_{AMC}\) \(= AD.DC -\frac{1}{2}AM.AC.sin{\alpha}\)
\(= AD.DC -\frac{1}{2}.\frac{AD}{cos{(\frac{\pi}{2}-2\alpha)}}.AC.sin{\alpha}\)
\(= AD.DC -\frac{1}{2}.\frac{AD}{cos{(\frac{\pi}{2}-2\alpha)}}.BC\)
\(= AD.DC -\frac{1}{2}.\frac{AD}{sin{2\alpha}}.BC\)
\(= AD.DC -\frac{1}{2}.\frac{AD}{2sin{\alpha}.cos{\alpha}}.BC\)
\(= AD.DC -\frac{1}{4}.\frac{AD}{\frac{BC.AB}{AC^2}}.BC\)
\(= AD.DC -\frac{1}{4}.\frac{AD.AC^2}{AB}\)
\(= AD.DC -\frac{1}{4}.\frac{AD.(AB^2+BC^2)}{AB}\) (1)
Thay \(AD=BC=210 mm\) và \(AB=DC=297mm\) vào (1), ta có:
\(S=210 \times297 - \frac{1}{4}.\frac{210.(297^2+210^2)}{297}\)\(≈38982\)\(mm^2\)
-/-
Trên đây là đáp án đề minh họa tham khảo tuyển sinh vào 10 môn Toán tỉnh An Giang năm 2020, mong rằng với nội dung này các em sẽ thử sức đề thi thử vào lớp 10 2020 môn toán và ôn luyện kiến thức thật tốt!
