Đề thi minh họa vào lớp 10 môn Toán tỉnh Thái Nguyên - Sở GD&ĐT Thái Nguyên vừa công bố đề thi tuyển sinh vào 10 môn Toán năm 2020 để giúp các em học sinh lớp 9 thử sức và ôn luyện trước với cấu trúc đề thi, cùng Đọc tài liệu tham khảo đề thi và đáp án dưới đây nhé:
Đề thi thử Toán vào 10 năm 2020 tỉnh Thái Nguyên lần 1
Câu 1: (1,0 điểm) Tìm điều kiện của x để biểu thức \(A=\sqrt{4-3x}-\sqrt[3]{x+1}\) có nghĩa.
Câu 2: (1,0 điểm) Không sử dụng máy tính cầm tay, giải phương trình sau:
\(x^2 - (3+\sqrt2)x +3\sqrt2 = 0\)
Câu 3: (1,0 điểm) Cho hàm số \(y =\frac{1}{2-m}x+2021\). Tìm các giá trị của m để hàm số đã cho là hàm số bậc nhất đồng biến trên ℝ.
Câu 4: (1,0 điểm) Đồ thị hàm số \(y=ax^2\) và đường thẳng \(y=2x+2\) cùng đi qua điểm có hoành độ là 1. Tìm giá trị của a.
Câu 5: (1,0 điểm) Cho biểu thức
\(B=\big( \frac{2x+1}{x\sqrt{x}-1} - \frac{\sqrt{x}}{x+\sqrt{x}+1} \big) \big(\frac{1+x\sqrt{x}}{1+\sqrt{x}}- \sqrt{x} \big)\) với \(x \geq 0 \) và \(x ≠ 1\)
a. Rút gọn B
b. Tìm x để B = 5
Câu 6: (1,0 điểm) Người ta đổ thêm 100g nước vào một dung dịch chứa 20g muối thì nồng độ của dung dịch giảm đi 10%. Hỏi trước khi đổ thêm nước thì dung dịch đó chứa bao nhiêu nước?
Câu 7: (1,0 điểm) Xác định tâm và tính bán kính đường tròn ngoại tiếp hình chữ nhật ABCD biết AB = 8cm, BC = 6cm.
Câu 8: (1,0 điểm)
Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 20cm, \(\frac{AB}{AC} =\frac {4}{3}\). Tính HB và HC.Câu 9: (1,0 điểm) Cho đường tròn (O), đường kính AB. Lấy điểm C nằm trên đường tròn (C ≠ A, C ≠ B). Các tiếp tuyến của đường tròn (O) tại A và C cắt nhau tại D. Gọi H là hình chiếu vuông góc của C trên đường thẳng AB. I là giao điểm của BD và CH. Chứng minh rằng CI = HI.
Câu 10: (1,0 điểm) Cho hai đường tròn (O) và (O') cắt nhau tại hai điểm A và B. Vẽ tiếp tuyến chung CD của hai đường tròn (C thuộc (O), D thuộc (O')). Lấy hai điểm E, F lần lượt thuộc các đường tròn (O), (O') sao cho ba điểm E, B, F thẳng hàng (B nằm giữa E và F, E ≠ B, F ≠ B) vầ EF song song với CD. Gọi P, Q lần lượt là giao điểm của các cặp đường thẳng DA với EF và CA với EF. K là giao điểm của hai đường thẳng EC và FD. Chứng minh rằng:
a. △ KCD = △ BCD
b. KP = KQ.
Trên đây là mẫu đề thi minh họa tuyển sinh vào 10 môn Toán tỉnh Thái Nguyên năm 2020 của Sở GD&ĐT vừa công bố.
Đáp án đề tham khảo vào 10 môn Toán năm 2020 - Thái Nguyên
Câu 1: (1,0 điểm) Tìm điều kiện của x để biểu thức \(A=\sqrt{4-3x}-\sqrt[3]{x+1}\) có nghĩa
Để A có nghĩa \(\Leftrightarrow 4-3x \geq 0\) \(\Leftrightarrow x \geq \frac{3}{4}\).
Câu 2: (1,0 điểm) Không sử dụng máy tính cầm tay, giải phương trình sau:
\(x^2 - (3+\sqrt2)x +3\sqrt2 = 0\)
Ta có: \(\Delta = (3+\sqrt{2} )^2 - 4 \times3\sqrt{2}\)
\(= 9 + 6\sqrt{2} + 2 - 12\sqrt{2}\)
\(= 9 - 6\sqrt{2} + 2\)
\(= (3-\sqrt{2} )^2 \)
Ta thấy \(\Delta > 0\) nên phương trình đã cho có 2 nghiệm phân biệt:
\(\left\{ \matrix{ x_1=\frac{3+\sqrt{2}-\sqrt{\Delta}}{2} \hfill \cr x_2=\frac{3+\sqrt{2}+\sqrt{\Delta}}{2} \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ x_1=\frac{3+\sqrt{2}-\sqrt{(3-\sqrt{2})^2}}{2} \hfill \cr x_2=\frac{3+\sqrt{2}+\sqrt{(3-\sqrt{2})^2}}{2} \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ x_1=\frac{3+\sqrt{2}-(3-\sqrt{2})}{2} \hfill \cr x_2=\frac{3+\sqrt{2}+(3-\sqrt{2})}{2} \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ x_1=\sqrt{2} \hfill \cr x_2=3 \hfill \cr} \right.\)
Vậy phương trình đã cho có 2 nghiệm phân biệt là \(x_1=\sqrt2\) và \(x_2=3\).
Câu 3: (1,0 điểm) Cho hàm số \(y =\frac{1}{2-m}x+2021\). Tìm các giá trị của m để hàm số đã cho là hàm số bậc nhất đồng biến trên \({\mathbb {R}}\)
Để hàm số đã cho là hàm bậc nhất đồng biến trên \({\mathbb {R}}\) \(\Leftrightarrow \frac {1}{2-m} >0\) \(\Leftrightarrow m <2\)
Câu 4: (1,0 điểm) Đồ thị hàm số \(y=ax^2\) và đường thẳng \(y=2x+2\) cùng đi qua điểm có hoành độ là 1. Tìm giá trị của a.
Gọi A là điểm mà cả 2 đồ thị trên đi qua có hoành độ là 1.
Ta có toạ độ của A là: \(\left\{ \matrix{ x=1 \hfill \cr y=2\times1+2=4 \hfill \cr} \right.\)
Thay toạ độ của A vào hàm số \(y=ax^2\), ta có: \(4=a\times1^2\) \(\Leftrightarrow a=4\)
Vậy \( a=4\).
Câu 5: (1,0 điểm) Cho biểu thức
\(B=\big( \frac{2x+1}{x\sqrt{x}-1} - \frac{\sqrt{x}}{x+\sqrt{x}+1} \big) \big(\frac{1+x\sqrt{x}}{1+\sqrt{x}}- \sqrt{x} \big)\)
với \(x \geq 0 \) và \(x ≠ 1\)a. Rút gọn B
Ta có:
\(B=\big( \frac{2x+1}{x\sqrt{x}-1} - \frac{\sqrt{x}}{x+\sqrt{x}+1} \big) \big(\frac{1+x\sqrt{x}}{1+\sqrt{x}}- \sqrt{x} \big)\)
\(=\big( \frac{2x+1}{(\sqrt{x}-1)(x+\sqrt{x}+1)} - \frac{\sqrt{x}}{x+\sqrt{x}+1} \big) \big(\frac{(1+\sqrt{x})(1-\sqrt{x}+x)}{1+\sqrt{x}}- \sqrt{x} \big)\)
\(=\big( \frac{2x+1}{(\sqrt{x}-1)(x+\sqrt{x}+1)} - \frac{\sqrt{x}(\sqrt{x}-1)}{(\sqrt{x}-1)(x+\sqrt{x}+1)} \big) \big(1-\sqrt{x}+x- \sqrt{x} \big)\)
\(=\big( \frac{2x+1-x+\sqrt{x}}{(\sqrt{x}-1)(x+\sqrt{x}+1)} \big) \big(1-2\sqrt{x}+x \big)\)
\(= \frac{x+\sqrt{x}+1}{(\sqrt{x}-1)(x+\sqrt{x}+1)} (\sqrt{x}-1 )^2\)
\(= \sqrt{x}-1\)
Vậy \(B = \sqrt{x}-1\)
b. Tìm x để B = 5
Để \(B=5\) \(\Leftrightarrow \sqrt{x}-1 = 5\) \(\Leftrightarrow \sqrt{x} = 6\) \(\Leftrightarrow x=36\) (thoả mãn đkxđ)
Vậy để \(B=5\) \(\Leftrightarrow x=36\)
Câu 6: (1,0 điểm) Người ta đổ thêm 100g nước vào một dung dịch chứa 20g muối thì nồng độ của dung dịch giảm đi 10%. Hỏi trước khi đổ thêm nước thì dung dịch đó chứa bao nhiêu nước?
Gọi số nước ban đầu của dung dịch đó có là A (g). (A>0)
Nồng độ của dung dịch đó ban đầu là: \(\frac{20}{A} \)
Nồng độ của dung dịch đó sau khi đổ thêm 100g nước là \(\frac{20}{A+100} \)
Vì khi đổ thêm 100g nước vào dung dịch đó chứa 20g muối thì nồng độ của dung dịch giảm đi 10%, tức là:
\(\frac{20}{A} - \frac{20}{A+100}= 0,1 \)
\(\Leftrightarrow \frac{20A+2000-20A}{A(A+100)} = 0,1 \)
\(\Leftrightarrow A^2+100A - 20000=0\)
\(\Leftrightarrow \left\{ \matrix{ A_1=100 \hfill \cr A_2=-200 \hfill \cr} \right.\)
Mà A>0 theo đkxđ nên \(A=100\).
Câu 7: (1,0 điểm) Xác định tâm và tính bán kính đường tròn ngoại tiếp hình chữ nhật ABCD biết AB = 8cm, BC = 6cm.
Kẻ đường chéo AC cắt BD tại O. Ta thấy O chính là tâm đường tròn ngoại tiếp hình chữ nhật ABCD.
Bán kính của đường tròn này là: \(R = OA = \frac{1}{2}AC\) \( = \frac{1}{2}\sqrt{AB^2+BC^2}\) \(=\frac{1}{2}\sqrt{8^2+6^2}\) \(=5\) (cm).
Câu 8: (1,0 điểm) Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 20cm, \(\frac{AB}{AC} =\frac {4}{3}\). Tính HB và HC.
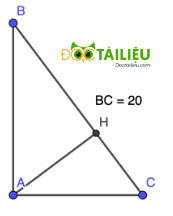
Ta có \(BC^2 = AB^2 + AC^2 \) \(= AB^2 + \big( \frac{3}{4}AB \big)^2\) \(\Leftrightarrow 20^2 = \frac{25}{16}AB^2\) \(\Leftrightarrow AB = \frac{20\times4}{5}=16\) (cm)
\(\Rightarrow AC = 12\) (cm)
Ta có: \(S_{\triangle ABC} = \frac {1}{2} AB.AC = \frac {1}{2} AH.BC\) \(\Leftrightarrow AH = \frac {AB.AC}{BC} \) \( = \frac {16\times12}{20} = \frac{48}{5}\) (cm)
Ta có: \(\triangle AHB ∽ \triangle CHA\) \(\Rightarrow \frac{AH}{CH} = \frac{HB}{HA} = \frac{AB}{AC} = \frac{4}{3} \) \(\Rightarrow \left\{ \matrix{ HC=\frac{3}{4}AH \hfill \cr HB=\frac{4}{3}AH \hfill \cr} \right.\) \(\Rightarrow \left\{ \matrix{ HC=\frac{3}{4}\times\frac{48}{5}= \frac{36}{5} \space (cm)\hfill \cr HB=\frac{4}{3}\times\frac{48}{5}=\frac{64}{5}\space (cm) \hfill \cr} \right.\)
Vậy \(HC = \frac{36}{5}\) cm và \(HB = \frac{64}{5}\) cm.
Câu 9: (1,0 điểm) Cho đường tròn (O), đường kính AB. Lấy điểm C nằm trên đường tròn (C ≠ A, C ≠ B). Các tiếp tuyến của đường tròn (O) tại A và C cắt nhau tại D. Gọi H là hình chiếu vuông góc của C trên đường thẳng AB. I là giao điểm của BD và CH. Chứng minh rằng CI = HI.
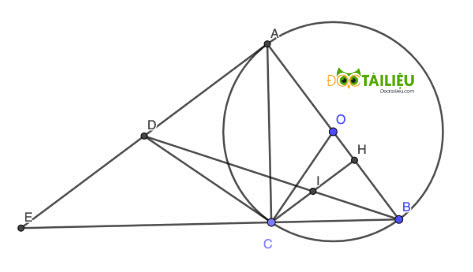
Kéo dài BC cắt AD tại E.
Xét đường tròn (O) có dây cung AC, ta có \(\angle ABC = \angle ACD \) (tính chất góc nội tiếp chắn cung) \(= \angle DAC\) (Tính chất DA DC là 2 tiếp tuyến của (O))
Lại có: \(\angle ACB = 90⁰\) (góc nội tiếp (O) chắn đường kính AB) \(\Rightarrow \angle ECD = 90⁰ - \angle DCA \) \(= 90⁰ - DAC = \angle AEC\) \(\Rightarrow \triangle EDC \) cân tại D hay \(DE = DC = DA\) \(\Rightarrow \) D là trung điểm AE.
Ta có \(CH \space //\space AE\) (cùng \(⊥ AB\)) nên xét tam giác BAE có \(CH \space //\space AE\) \(\Rightarrow \frac{HC}{AE}=\frac{HB}{AB}\)
Tương tự với tam giác ADB, ta có \( \frac{HI}{AD}=\frac{HB}{AB}\)
Suy ra \( \frac{HI}{AD}=\frac{HC}{AE}\) \(\Rightarrow \frac{HI}{HC}=\frac{AD}{AE} = \frac{1}{2}\) \(\Rightarrow HI = CI\) (đpcm)
Câu 10: (1,0 điểm) Cho hai đường tròn (O) và (O') cắt nhau tại hai điểm A và B. Vẽ tiếp tuyến chung CD của hai đường tròn (C thuộc (O), D thuộc (O')). Lấy hai điểm E, F lần lượt thuộc các đường tròn (O), (O') sao cho ba điểm E, B, F thẳng hàng (B nằm giữa E và F, E ≠ B, F ≠ B) vầ EF song song với CD. Gọi P, Q lần lượt là giao điểm của các cặp đường thẳng DA với EF và CA với EF. K là giao điểm của hai đường thẳng EC và FD. Chứng minh rằng:
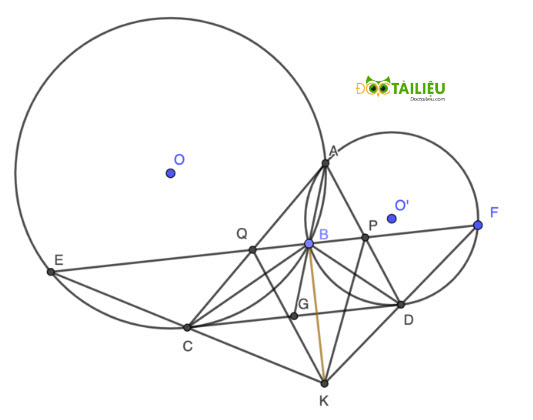
a. \(\triangle KCD = \triangle BCD\)
Theo tiên đề ơ-clit cho \(CD \space // \space EF\), với đường thẳng KF, ta có \(\angle KDC = \angle KFE\)
Xét đường tròn (O') có CD là tiếp tuyến \(\Rightarrow \angle CDB = \angle DAB = \angle DFB \) (tính chất góc nội tiếp chắn cung BD) \(= \angle KFE \)
Suy ra \(\angle KDC = \angle CDB \)
Chứng minh tương tự ta có \(\angle KCD = \angle DCB \)
Xét tam giác KCD và BCD, ta có: \(\left\{ \matrix{ \angle KDC = \angle CDB \hfill \cr \angle KCD = \angle DCB \hfill \cr DC \space chung \hfill \cr} \right.\) \(\Rightarrow \triangle KCD = \triangle BCD\) (g.c.g) (đpcm)
b. \(KP = KQ\)
Theo ý a, ta có \(\triangle KCD = \triangle BCD\) \(\Rightarrow KD=BD\)
Lại có \(CD \space // \space EF\) (gt) \(\Rightarrow O'D ⊥ EF \) hay \(O'D ⊥ BF\).
Theo tính chất của dây cung đường tròn, ta dễ thấy \(BD = DF\) \(\Rightarrow KD=BD = DF\) \(\Rightarrow \triangle KBF\) vuông tại B.
\(\Rightarrow KB ⊥ EF \) hay \( KB ⊥ QP\)
Xét tam giác GDB và GAD, có:
\(\left\{ \matrix{ \angle BDG = \angle GAD \space (cm \space p.a) \hfill \cr \angle BGD \space chung \hfill \cr} \right.\) \(\Rightarrow \triangle GDB ∽ \triangle GAD\) \(\Rightarrow \frac{GD}{GB} = \frac{GA}{GD}\) \(\Rightarrow GD^2 = GA.GB\)
Chứng minh tương tự cho tam giác GCB và GAC ta có \( GC^2 = GA.GB\)
Suy ra \(GD = GC \) (cùng \(= \sqrt {GA.GB}\)) hay G là trung điểm CD.
Tam giác ACD có \(CD \space // \space EF\) hay \(QP \space // \space CD\), có G là trung điểm CD, AG cắt QP tại B \(\Rightarrow\) B là trung điểm QP.
Xét tam giác QKP có \(KB ⊥ QP\) mà B là trung điểm QP \(\Rightarrow\) tam giác QKP cân tại K \(\Rightarrow\) \(KP = KQ\) (đpcm)
Trên đây là hướng dẫn giải chi tiết đề thi thử vào 10 môn toán năm 2020 tỉnh Thái Nguyên lần 1, mong rằng đây sẽ là tài liệu hữu ích giúp các em ôn tập. Đừng quên còn rất nhiều tài liêu đề thi thử vào lớp 10 môn toán khác của các tỉnh thành trên cả nước nhé.
