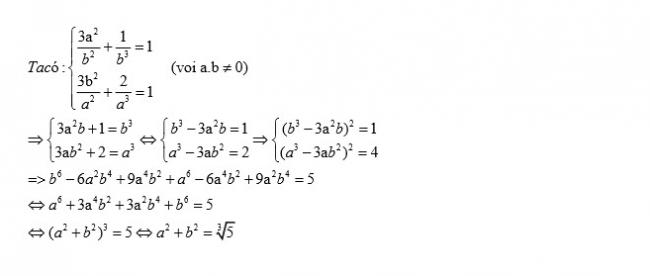Đề thi:
Đáp án:
Câu 1:
Câu 4:
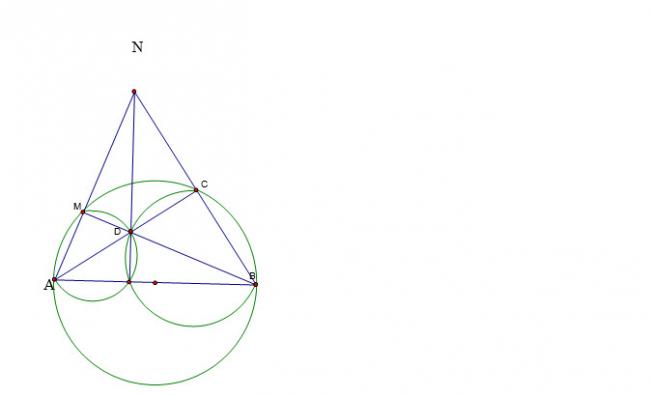
1/ AC vuông góc NB (Vì ACB là góc nội tiếp chắn nửa đường tròn) BM vuông góc NA (Vì AMB là góc nội tiếp chắn nửa đường tròn)
Do đó từ giác CDMN nội tiếp (tứ giác có tổng hai góc đối bằng 180 độ) 2/ Hai tam giác ADM và BDC đồng dạng nên AM.BD=AD.BC
3/ Gọi I’ là giao điểm của DN với AB.
Tam giác ABN có các đường cao AC, BM cắt nhau tại D nên ND vuông góc với AB tại I’.
Chứng minh tứ giác BCDI’ nội tiếp suy ra I’ thuộc đường tròn ngoại tiếp tam giác BCD. (1)
Chứng minh tứ giác AMDI’ nội tiếp suy ra I’ thuộc đường tròn ngoại tiếp tam giác AMD. (2)
Từ (1) và (2) suy ra I’ là giao điểm của đường tròn ngoại tiếp tam giác BCD và đường tròn ngoại tiếp tam giác AMD. Do đó I’ trùng với I. Vậy 3 điểm N; D; I thẳng hàng.
Câu 5:
dap an de thi toan vao lop 10 2017 quang ninh
dap an de thi toan vao lop 10 2017 quang ninh