Sáng 16/5, Ninh Bình đã tổ chức kỳ thi thử tuyển sinh vào 10 môn Toán năm 2020 lần 1, cùng Đọc tài liệu tham khảo đề thi và đáp án dưới đây nhé:
Đề thi thử Toán vào 10 năm 2020 tỉnh Ninh Bình lần 1
Câu 1 (2,0 điểm).
Cho hàm số \(y = mx +n\) (1) (m, n là tham số, m ≠ 0) có đồ thị là đường thẳng (d).a) Hãy chỉ ra hệ số góc của đường thẳng (d).
b) Tìm điều kiện của m để hàm số (1) nghịch biến trên R.
c) Tim m, n để đường thẳng (d) đi qua hai điểm A(1;3) và B(2;5).
Câu 2 (2,0 điểm). Cho biểu thức \(S = \dfrac{2\sqrt{x}}{x-2\sqrt{x}} + \dfrac{3\sqrt{x}-14}{x-4}\) với \(x > 0, x ≠ 4\)
a) Rút gọn \(\dfrac{2\sqrt{x}}{x-2\sqrt{x}}\)
b) Rút gọn biểu thức S.
c) Tìm tất cả các giá trị của x để biểu thức S nhận giá trị nguyên.
Câu 3 (1,5 điểm). Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình.
Có 2 loại dung dịch muối ăn, một loại chứa 1% muối ăn và loại còn lại chứa 3,5% muối ăn, Hỏi cần lấy bao nhiêu cân dung dịch mỗi loại trên để hoà lẫn với nhau tạo thành 140 cân dung dịch chứa 3% muối ăn?
Câu 4 (4,0 điểm).
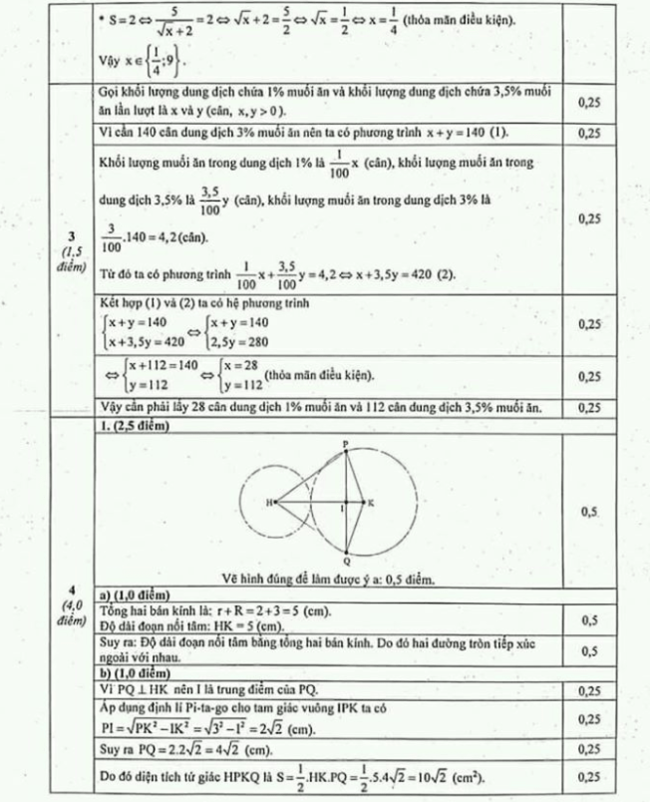
1.Cho đoạn thẳng HK = 5cm. Vẽ đường tròn tâm H, bán kính 2cm và đường tròn tâm K, bản kính 3cm.
a) Xác định vị trí tương đối của hai đường tròn trên.
b) Trên đoạn thẳng HK lấy điểm D sao cho IK = 1cm. Vẽ đường thẳng đi qua I và vuông góc với HK, đường thẳng này cắt đường tròn (K) tại hai điểm P, Q. Tính diện tích tứ giác HPKQ.
2. Một bể cá làm bằng kính dạng hình hộp chữ nhật có thể tích là 500dm và chiều cao là 5cm (bỏ qua chiều dày của kính làm bể cá).
a) Tính diện tích đáy của bể cá trên.
b) Đáy của bể cá trên có thể có chu vi nhỏ nhất bằng bao nhiêu? Tại sao?
Câu 5 (0,5 điểm). Cho các số thực dương a, b, c thỏa mãn abc = 1. Tìm giá trị lớn nhất của biểu thức
T = \(\dfrac{1}{\sqrt[3]{a} + \sqrt[3]{b}+1} + \dfrac{1}{\sqrt[3]{b} + \sqrt[3]{c}+1} + \dfrac{1}{\sqrt[3]{c} + \sqrt[3]{a}+1}\)
Vậy là so với cấu trúc đề thi thử vào 10 môn Toán của tỉnh Ninh Bình năm 2020 trong lần thứ nhất đều không có thay đổi so với cấu trúc đề tuyển sinh vào lớp 10 các năm. Hãy thử sức làm bài trong thời gian 120 phút rồi so sánh đối chiếu với lời giải chi tiết dưới đây sau em nhé.
Đáp án vào 10 môn Toán năm 2020 tỉnh Ninh Bình lần thứ nhất

2) (1,5 điểm)
a) (1,0 điểm)
Diện tích đáy của bể cá là S = V/h
Thay số \(S = 500/5 = 100 (dm^2)\)
b) (0,5 điểm)
Gọi a.b là độ dài hai cạnh của đáy bể cá (\(dm; a, b > 0\))
Theo kết quả ở ý a) thì \(ab=100 (dm^2)\)
Áp dụng bất đẳng thức Cô-si ta có \(2(a+b) ≥ 2.2\sqrt{ab}=4\sqrt{100}40\)
Dấu bằng xảy ra khi a=b=10
Vậy đáy của bể cá có thể có chu vi nhỏ nhất bằng 40 (dm).
Câu 5 (0,5 điểm).
Đặt \( \sqrt[3]{a}=x^3, \sqrt[3]{b}=y^3, \sqrt[3]{c}=z^3 \)=> \(x,y,z>0\) và xyz=1
Ta có \(x^3 + y^3=(x+y)(x^2+y^2-xy)≥xy(x+y)\) do \(x^2+y^2≥2xy\) theo Cô-si.
Từ đó suy ra \(\dfrac{1}{x^3 + y^3+1}≤\dfrac{xyz}{xy(x+y)+xyz}= \dfrac{z}{x+y+z} (1)\)
Tương tự
\(\dfrac{1}{y^3 + z^3+1}≤\dfrac{x}{x+y+z}\) (2)
\(\dfrac{1}{z^3 + x^3+1}≤\dfrac{y}{x+y+z}\) (3)
Cộng vế với vế của 3 bất đẳng thức
\(T = \dfrac{1}{x^3 + y^3+1} + \dfrac{1}{y^3 + z^3+1} + \dfrac{1}{z^3 + x^3+1} ≤ \dfrac{x+y+z}{x+y+z}=1\)
Dấu đẳng thức xảy ra khi x = y = z = 1 hay a = b = c = 1.
Vậy T đạt giá trị lớn nhất bằng 1.
Trên đây là hướng dẫn giải chi tiết đề thi thử vào 10 môn toán năm 2020 tỉnh Ninh Bình lần 1, mong rằng đây sẽ là tài liệu hữu ích giúp các em ôn tập. Đừng quên còn rất nhiều tài liêu đề thi thử vào 10 môn toán khác của các tỉnh thành trên cả nước nhé.
