Cùng Đọc tài liệu thử sức với đề thi thử tuyển sinh vào lớp 10 môn toán năm 2020 có đáp án của GD&ĐT tỉnh Quảng Nam vừa diễn ra ngày 29/6/2020 em nhé:
Đề thi thử
Mã đề: A
SỞ GD&ĐT QUẢNG NAM ĐỀ CHÍNH THỨC | KIỂM TRA HỌC KỲ II LỚP 9 NĂM HỌC 2019 - 2020 MÔN:Toán Thời gian làm bài: 60 phút (Không kể thời gian giao đề) |
PHẦN I/ Trắc nghiệm
(Đáp án trong ảnh đề thi dưới đây là đáp án của thí sinh, xem đáp án bên dưới nhé)

A. 45π cm²
B. 45π cm³
C. 90π cm²
D. 90π cm³
PHẦN II/ Tự luận.
Bài 1: (1,25 điểm)
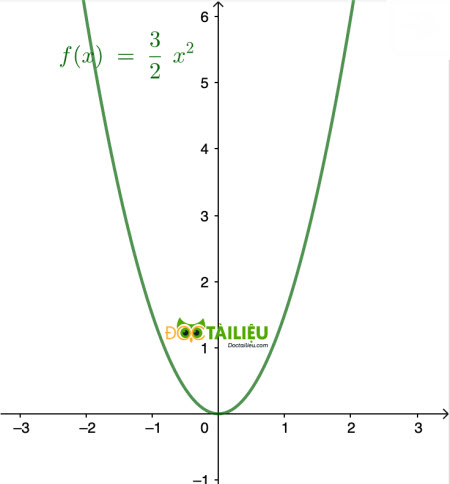
a) Vẽ đồ thị hàm số: \(y = \dfrac{3}2 x^2\)
b) Giải phương trình:
\(x^4 - 3x^2 - 4 = 0\)
Bài 2: (1,25 điểm)
Một khu vườn hình chữ nhật có chiều dài lớn hơn chiều rộng 14m và diện tích bằng 95m². Tính chiều dài và chiều rộng của khu vườn đó.
Bài 3: (2,5 điểm)
Cho tam giác ABC (có ba góc nhọn) nội tiếp đường tròn (O) và tia phân giác của góc B cắt đường tròn tại M. Các đường cao BD và CK của △ABC cắt nhau tại H.
a) Chứng minh rằng tứ giác ADHK nội tiếp một đường tròn.
b) Chứng minh rằng OM là tia phân giác của góc AOC.
c) Gọi I là giao điểm của OM và AC. Tính tỉ số \(\dfrac{OI}{BH}\).
Đáp án
Mã đề A
PHẦN I/ Trắc nghiệm
1. D 2. B 3. A 4. A 5. D | 6. D 7. C 8. B 9. C 10. B | 11. A 12. C 13. A 14. C 15. B |
PHẦN II/ Tự luận.
Bài 1:
a) Vẽ đồ thị hàm số: \(y = \dfrac{3}2 x^2\)
b)
\(x^4 - 3x^2 - 4 = 0\)
\(\Leftrightarrow (x^2 -4)(x^2+1) = 0\)
\(\Leftrightarrow x^2 = 4\) (vì \(x^2+1\geq 1 > 0\))
\(\Leftrightarrow x = ±2\)
Bài 2:
Gọi chiều rộng của khu vườn đó là A (mét, A > 0)
Chiều dài của khu vườn đó là A + 14 (m)
Diện tích khu vườn:
\(S = A(A+14) = 95 \Leftrightarrow A^2 + 14 A - 95 = 0\)
\(\Leftrightarrow \left[ \matrix{ A = 5 \space (tm) \hfill \cr A = -19 \space (loại) \hfill \cr} \right.\)
⇒ A = 5(m) ⇒ Chiều dài khu vườn là 5 + 14 = 19 (m).
KL....
Bài 3:
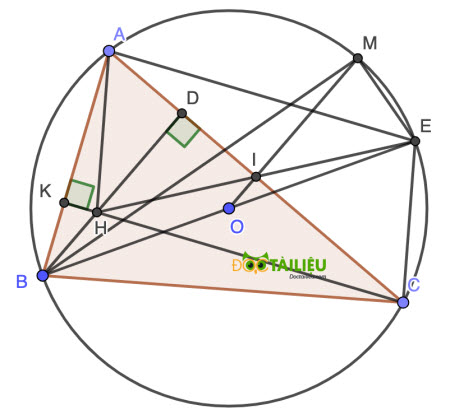
a)
Vì BD và CK là đường cao của △ABC ⇒ ∠AKH = ∠ADH = 90° ⇒ K và D cùng thuộc đường tròn đường kính AH, hay tứ giác ADHK nội tiếp (đpcm).
b)
Vì BM là phân giác trong góc ABC ⇒ ∠ABM = ∠CBM (1)
Lại có \(∠ABM = \dfrac{1}2 ∠AOM\) (vì cùng \( = \dfrac{1}2 \stackrel\frown{AM}\)) (2)
Tương tự ta có \(∠CBM = \dfrac{1}2 ∠MOC\) (vì cùng \( = \dfrac{1}2 \stackrel\frown{MC}\)) (3)
Từ (1) (2) và (3) ta có: ∠AOM = ∠MOC ⇒ OM là tia phân giác của góc AOC (đpcm).
c)
Ta có OM là tia phân giác của góc AOC ⇒ M là điểm chính giữa cung AC ⇒ OM ⊥ AC tại I, đồng thời I là trung điểm AC.
Mà BD ⊥ AC ⇒ BH // IO.
Vẽ đường kinh BE.
Ta có ∠BCE = 90° (góc nội tiếp chắn đường kính) ⇒ EC ⊥ BC.
Lại có AH ⊥ BC (Do H là trực tâm của △ABC) ⇒ EC // AH (*)
Tương tự ta có EA ⊥ AB, CH ⊥ AB ⇒ EA // CH (**)
Từ (*) và (**) suy ra AECH là hình bình hành ⇒ AC cắt EH tại trung điểm của nhau, mà I là trung điểm AC (cmt) ⇒ I,E,H thẳng hàng.
Xét △EBH có IO // BH, O là trung điểm BE ⇒ \(\dfrac{OI}{BH} = \dfrac{1}2\) (tính chất đường trung bình).
Mã đề B
1. C 2. A 3. AB 4. C 5. D | 6. C 7. D 8. C 9. A 10. D | 11. B 12. B 13. C 14. B 15. C |
-/-
Trên đây là hướng dẫn giải chi tiết đề thi khảo sát chất lượng học kì 2 dành cho học sinh lớp 9 tại Quảng Nam mong rằng đây sẽ là tài liệu hữu ích giúp các em ôn tập. Đừng quên còn rất nhiều tài liêu đề thi thử vào lớp 10 môn toán khác của các tỉnh thành trên cả nước nhé.
