Công thức lượng giác lớp 10 và bài tập chi tiết đầy đủ nhất

Các công thức lượng giác lớp 10 và những dạng bài tập cơ bản được tổng hợp chi tiết giúp các em học tốt hơn.

I Bảng giá trị lượng giác của một số cung hay góc đặc biệt

1. Bảng giá trị lượng giác

Bảng các giá trị sin, cos, tan, cot thuộc góc phần tư thứ nhất

Giá trị | Góc $\alpha$	$0\left(0^{\circ}\right)$	$\frac{\pi}{6}\left(30^{\circ}\right)$	$\frac{\pi}{4}\left(45^{0}\right)$	$\frac{\pi}{3}\left(60^{\circ}\right)$	$\frac{\pi}{2}\left(90^{\circ}\right)$
$\sin \alpha$	0	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$	1
$\cos \alpha$	1	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$	0
$\tan \alpha$	0	$\frac{\sqrt{3}}{2}$	1	$\sqrt{3}$	II
$\cot \alpha$	II	$\sqrt{3}$	1	$\frac{\sqrt{3}}{2}$	0

2. Cung và góc lượng giác

 

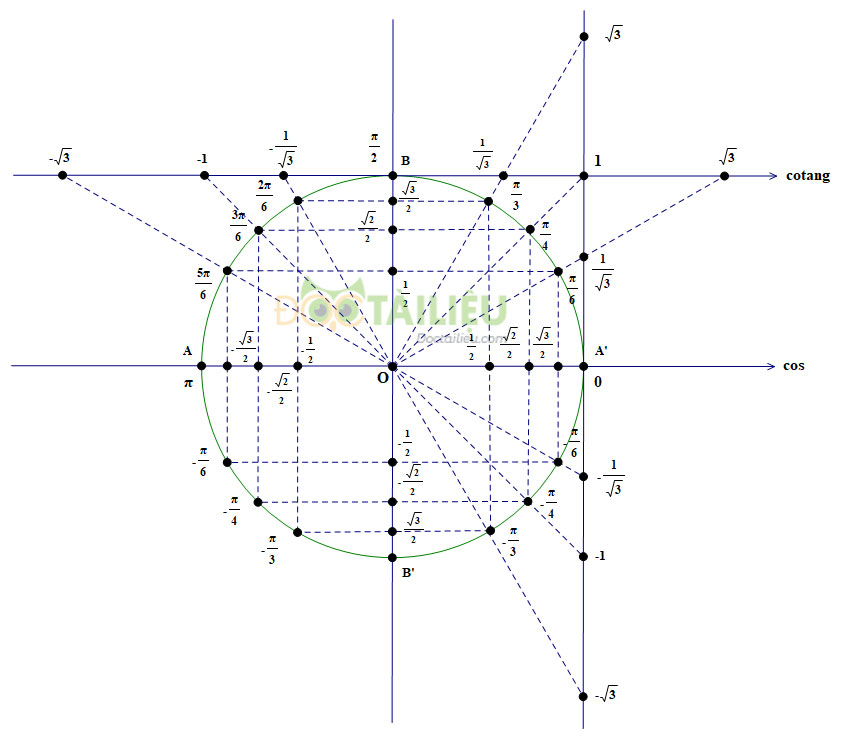
Hai góc đối nhau α và −α

$\begin{array}{l} \sin (-\alpha)=-\sin \alpha \\ \cos (-\alpha)=\cos \alpha \\ \operatorname{tg}(-\alpha)=-\operatorname{tg}(\alpha) \\ \operatorname{cotg}(-\alpha)=-\operatorname{cotg}(\alpha) \end{array}$

Hai góc bù nhau: α và π − α

$\begin{array}{l} \sin (\pi-\alpha)=\sin \alpha \\ \cos (\pi-\alpha)=-\cos \alpha \\ \operatorname{tg}(\pi-\alpha)=-\operatorname{tg} \alpha \\ \operatorname{cotg}(\pi-\alpha)=-\operatorname{cotg} \alpha \end{array}$

Hai góc hơn kém π: α và π + α

$\begin{array}{l} \sin (\pi+\alpha)=-\sin \alpha \\ \cos (\pi+\alpha)=-\cos \alpha \\ \operatorname{tg}(\pi+\alpha)=\operatorname{tg} \alpha \\ \operatorname{cotg}(\pi+\alpha)=\operatorname{cotg} \alpha \end{array}$

Hai góc phụ nhau: α và π/2 – α

$\begin{array}{l} \sin \left(\frac{\pi}{2}-\alpha\right)=\cos \alpha \\ \cos \left(\frac{\pi}{2}-\alpha\right)=\sin \alpha \\ \operatorname{tg}\left(\frac{\pi}{2}-\alpha\right)=\cot g \alpha \\ \cot g\left(\frac{\pi}{2}-\alpha\right)=\operatorname{tg} \alpha \end{array}$

Hai góc hơn kém nhau π/2

$\begin{array}{l} \sin \left(\frac{\pi}{2}+\alpha\right)=\cos \alpha \\ \cos \left(\frac{\pi}{2}+\alpha\right)=-\sin \alpha \\ \operatorname{tg}\left(\frac{\pi}{2}+\alpha\right)=-\cot g \alpha \\ \operatorname{cotg}\left(\frac{\pi}{2}+\alpha\right)=-\operatorname{tg} \alpha \end{array}$

II Tổng hợp 10 công thức lượng giác lớp 10 cơ bản

Dưới đây là các công thức lượng giác cơ bản nằm trong chương trình học môn Toán lớp 10, các em cần phải ghi nhớ để có thể hoàn thành tốt các bài tập liên quan:

1. Hệ thức cơ bản

$\begin{array}{l} \sin ^{2} \alpha+\cos ^{2} \alpha=1 \\ \tan \alpha \cdot \cot \alpha=1 \quad\left(\alpha \neq k \frac{\pi}{2}, k \in Z \right) \\ 1+\tan ^{2} \alpha=\frac{1}{\cos ^{2} \alpha}\left(\alpha \neq \frac{\pi}{2}+k \pi, k \in Z \right) \\ 1+\cot ^{2} \alpha=\frac{1}{\sin ^{2} \alpha} \quad(\alpha \neq k \pi, k \in Z ) \\ \tan \alpha=\frac{\sin \alpha}{\cos }, \cot \alpha=\frac{\cos \alpha}{\sin \alpha} \end{array}$

2. Công thức cung liên kết

   Toàn bộ các công thức lượng giác được sử dụng trong chương trình liên quan và được áp dụng cả trong quá trình học của các em sau này.

Công thức hai cung đối nhau $(\alpha \text { và } -\alpha)$

$\begin{array}{l} \cos (-\alpha)=\cos \alpha \\ \sin (-\alpha)=-\sin \alpha \\ \tan (-\alpha)=-\tan \alpha \\ \cot (-\alpha)=-\cot \alpha \end{array}$

Công thức hai cung bù nhau $(\alpha \text { và } \pi-\alpha)$

$\begin{array}{l} \sin (\pi-\alpha)=\sin \alpha \\ \cos (\pi-\alpha)=-\cos \alpha \\ \tan (\pi-\alpha)=-\tan \alpha \\ \cot (\pi-\alpha)=-\cot \alpha \end{array}$

Công thức hai góc phụ nhau $\left(\alpha \text { và } \frac{\pi}{2}-\alpha\right)$

$\begin{array}{l} \sin \left(\frac{\pi}{2}-\alpha\right)=\cos \alpha \\ \cos \left(\frac{\pi}{2}-\alpha\right)=\sin \alpha \\ \tan \left(\frac{\pi}{2}-\alpha\right)=\cot \alpha \\ \cot \left(\frac{\pi}{2}-\alpha\right)=\tan \alpha \end{array}$

Công thức hai góc hơn, kém nhau π

$\begin{array}{l} \sin (\pi+\alpha)=-\sin \alpha \\ \cos (\pi+\alpha)=-\cos \alpha \\ \tan (\pi+\alpha)=\tan \alpha \\ \cot (\pi+\alpha)=\cot \alpha \end{array}$

Công thức cung hơn kém $\frac{\pi}{2}$

$\begin{array}{l} \cos \left(\frac{\pi}{2}+\alpha\right)=-\sin \alpha \\ \sin \left(\frac{\pi}{2}+\alpha\right)=\cos \alpha \end{array}$

3. Công thức cộng

$\begin{array}{l} \sin (a \pm b)=\sin a \cos b \pm \cos a \sin b \\ \cos (a \pm b)=\cos a \cos b \sin a \sin b \\ \tan (a \pm b)=\frac{\tan \alpha \pm \tan b}{1 \mp \tan a \cdot \tan b} \end{array}$

Cách nhớ : sin thì sin cos cos sin, cos thì cos cos sin sin dấu trừ, tan thì tan nọ tan kia chia cho mẫu số một trừ tan tan

4. Công thức nhân đôi

$\begin{array}{l} \sin 2 x=2 \sin x \cdot \cos x \\ \cos 2 x=\cos ^{2} x-\sin ^{2} x=2 \cos ^{2} x-1=1-2 \sin ^{2} x \\ \tan 2 x=\frac{2 \tan x}{1-\tan ^{2} x} \quad \cot 2 x=\frac{\cot ^{2} x-1}{2 \cot x} \end{array}$

5. Công thức nhân ba

$\begin{array}{l} \sin 3 x=3 \sin x-4 \sin ^{3} x \\ \cos 3 x=4 \cos ^{3} x-3 \cos x \end{array}$

6. Công thức hạ bậc

$\begin{array}{lll} \sin ^{2} a=\frac{1}{2}(1-\cos 2 a) & \cos ^{2} a=\frac{1}{2}(1+\cos 2 a) & \tan ^{2} a=\frac{1-\cos 2 a}{1+\cos 2 a} \\ \sin ^{3} a=\frac{3 \sin a-\sin 3 a}{4} & \cos ^{3} a=\frac{3 \cos a+\cos 3 a}{4} \end{array}$

7. Công thức tính tổng và hiệu của sin a và cos a

$\begin{array}{l} \sin x+\cos x=\sqrt{2} \cdot \sin \left(x+\frac{\pi}{4}\right) \\ \sin x-\cos x=\sqrt{2} \cdot \sin \left(x-\frac{\pi}{4}\right) \end{array}$

8. Công thức chia đôi

$\begin{array}{l} \text { Đặt } t=\operatorname{tg} \frac{a}{2}(\text { vói } a \neq \pi+k 2 \pi) \\ \text { sin } a=\frac{2 t}{1+t^{2}} \\ \cos a=\frac{1-t^{2}}{1+t^{2}} \\ \text { tga }=\frac{2 t}{1-t^{2}} \end{array}$

9. Công thức biến đổi tổng thành tích

$\begin{array}{l} \cos a+\cos b=2 \cos \frac{a+b}{2} \cos \frac{a-b}{2} \\ \cos a-\cos b=-2 \sin \frac{a+b}{2} \sin \frac{a-b}{2} \\ \sin a+\sin b=2 \sin \frac{a+b}{2} \cos \frac{a-b}{2} \\ \sin a-\sin b=2 \cos \frac{a+b}{2} \sin \frac{a-b}{2} \\ \tan a \pm \tan b=\frac{\sin (a \pm b)}{\cos a \cos b} \quad\left(a, b \neq \frac{\pi}{2}+k \pi, k \in Z \right) \\ \cot a \pm \cot b=\frac{\sin (b \pm a)}{\sin a \sin b} \quad(a, b \neq k \pi, k \in Z ) \\ \tan a+\cot b=\frac{\sin (a-b)}{\cos a \sin b} \quad\left(a \neq \frac{\pi}{2}+k \pi, b \neq l \pi, k, l \in Z \right) \\ \cot a-\tan b=\frac{\cos (a+b)}{\sin a \cos b} \quad\left(a \neq k \pi, b \neq \frac{\pi}{2}+l \pi, k, l \in Z \right) \end{array}$

10. Công thức biến đổi tích thành tổng

$\begin{array}{l} \cos a \cos b=\frac{1}{2}[\cos (a+b)+\cos (a-b)] \\ \sin a \sin b=-\frac{1}{2}[\cos (a+b)-\cos (a-b)] \\ \sin a \cos b=\frac{1}{2}[\sin (a+b)+\sin (a-b)] \\ \cos a \sin b=\frac{1}{2}[\sin (a+b)-\sin (a-b)] \end{array}$

III 4 công thức lượng giác lớp 10 nâng cao

   Những công thức lượng giác nâng cao thường xuyên gặp phải trong các bài toán rút gọn biểu thức, chứng minh biểu thức, giải phương trình lượng giá...

1. Công thức lượng giác sử dụng biến đổi hẳng đẳng thức

$\sin ^{3} x+\cos ^{3} x=(\sin x+\cos x)\left(\sin ^{2} x-\sin x \cdot \cos x+\cos ^{2} x\right)$

$\begin{aligned} \sin ^{4} x+\cos ^{4} x &=\left(\sin ^{2} x+\cos ^{2} x\right)^{2}-2 \sin ^{2} x \cdot \cos ^{2} x \\ &=1-\frac{1}{2} \sin ^{2}(2 x)=\frac{3}{4}+\frac{1}{4} \cdot \cos (4 x) \end{aligned}$

$\begin{aligned} \sin ^{6} x+\cos ^{6} x &=\left(\sin ^{2} x+\cos ^{2} x\right)^{2}-3 \sin ^{2} x \cdot \cos ^{2} x \\ &=1-\frac{3}{4} \sin ^{2}(2 x)=\frac{5}{8}+\frac{3}{8} \cos (4 x) \end{aligned}$

$\sin ^{4} x-\cos ^{4} x=-\cos (2 x)$

2. Công thức hạ bậc nâng cao

$\sin ^{3} x=\frac{3 \sin x-\sin (3 x)}{4}$

$\cos ^{3} x=\frac{3 \cos x+\cos (3 x)}{4}$

$\tan ^{2} x=\frac{1-\cos (2 x)}{1+\cos (2 x)}$

$\tan ^{3} x=\frac{3 \sin x-\sin (3 x)}{3 \cos x+\cos (3 x)}$

3. Công thức liên quan đến tổng và hiệu các giá trị lượng giác

Mối liên hệ giữa sin và cos

$\begin{array}{l} \sin x+\cos x=\sqrt{2} \sin \left(x+\frac{\pi}{4}\right)=\sqrt{2} \cos \left(x-\frac{\pi}{4}\right) \\ \sin x-\cos x=\sqrt{2} \sin \left(x-\frac{\pi}{4}\right)=\sqrt{2} \cos \left(x+\frac{\pi}{4}\right) \\ \cos x-\sin x=\sqrt{2} \sin \left(\frac{\pi}{4}-x\right)=\sqrt{2} \cos \left(x+\frac{\pi}{4}\right) \end{array}$

Mối liên hệ giữa tan và cot

$\begin{array}{ll} \tan x+\tan y=\frac{\sin (x+y)}{\cos x \cdot \cos y} & \tan x-\tan y=\frac{-\sin (x-y)}{\cos x \cdot \cos y} \\ \cot x+\cot y=\frac{\sin (x+y)}{\sin x \cdot \sin y} & \cot x-\cot y=\frac{-\sin (x-y)}{\sin x \cdot \sin y} \\ \tan x+\tan y=\frac{\sin (x-y)}{\cos x \cdot \cos y} & \cot x-\tan y=\frac{\cos (x+y)}{\sin x \cdot \cos y} \\ \tan x+\cot x=\frac{2}{2 \sin (2 x)} & \cot x-\tan x=2 \cot (2 x) \end{array}$

4. Các hệ thức lượng giác cơ bản trong tam giác

$\text { 1) } \sin A+\sin B+\sin C=4 \cos \frac{A}{2} \cos \frac{B}{2} \cos \frac{C}{2} \text { . }$

$\text { 2) } \sin 2 A+\sin 2 B+\sin 2 C=4 \sin A \sin B \sin C \text { . }$

$\text { 3) } \sin ^{2} A+\sin ^{2} B+\sin ^{2} C=2(1+\cos A \cos B \cos C) \text { . }$

$\text { 4) } \cos A+\cos B+\cos C=1+4 \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2}$

$\text { 5) } \cos 2 A+\cos 2 B+\cos 2 C=-1-4 \cos A \cos B \cos C \text { . }$

$\text { 6) } \cos ^{2} A+\cos ^{2} B+\cos ^{2} C=1-2 \cos A \cos B \cos C \text { . }$

$\text { 7) } \tan A+\tan B+\tan C=\tan A \tan B \tan C$ (ABC là tam giác không vuông)

$\text { 8) } \cot \frac{A}{2}+\cot \frac{B}{2}+\cot \frac{C}{2}=\cot \frac{A}{2} \cot \frac{B}{2} \cot \frac{C}{2} \text { . }$

$\text { 9) } \tan \frac{A}{2} \tan \frac{B}{2}+\tan \frac{B}{2} \tan \frac{C}{2}+\tan \frac{C}{2} \tan \frac{A}{2}=1 \text { . }$

$\text { 10) } \cot A \cot B+\cot B \cot C+\cot C \cot A=1$

  Trên đây là tổng hợp các công thức lượng giác nâng cao toán lớp 10 được chia sẻ với mong muốn giúp các em học sinh giỏi ôn tập và hoàn thành tốt các bài tập nâng cao...

IV Cách học thuộc công thức lượng giác lớp 10 dễ nhớ.

1. Cách nhớ công thức cộng

a) Công thức cộng liên quan tới cos và sin

Cos thì cos cos sin sin
Sin thì sin cos cos sin rõ ràng
Cos thì đổi dấu hỡi nàng
Sin thì giữ dấu xin chàng nhớ cho!

b) Công thức cộng liên quan tới tan và cot

Tan một tổng hai tầng cao rộng
Trên thượng tầng tan cộng cùng tan
Hạ tầng số 1 ngang tàng
Dám trừ đi cả tan tan oai hùng

2. Cách ghi nhớ giá trị lượng giác của các cung liên quan đặc biệt

cos đối: cos( – x ) = cosx
sin bù: sin( π – x ) = sina
Phụ chéo là 2 góc phụ nhau thì sin góc này bằng cos góc kia, tan góc này băng cot góc kia.
Hơn kém π tan: tan(x + π) = tanx và cot(x + π) = cotx

3. Cách ghi nhớ công thức biến đổi tích thành tổng

Cos cos nửa cos-cộng, cộng cos-trừ
Sin sin nửa cos-trừ trừ cos-cộng
Sin cos nửa sin-cộng cộng sin-trừ.

4. Cách ghi nhớ công thức nhân đôi

Sin gấp đôi bằng 2 sin cos
Cos gấp đôi bằng bình phương cos trừ đi bình sin
Bằng trừ 1 cộng hai bình cos
Bằng cộng 1 trừ hai bình sin
Tan gấp đôi bằng Tan đôi ta lấy đôi tan (2 tan )
Chia một trừ lại bình tan, ra liền.

V Các dạng bài tập lượng giác lớp 10 cơ bản có đáp án

Dưới đây là 7 dạng bài tập lượng giác thường gặp nhất:

Dạng 1: Tính giá trị lượng giác của góc, hay cho trước 1 giác trị tính các giá trị lượng giác còn lại

Phương pháp giải : Sử dụng các công thức lượng giác cơ bản

Ví dụ 1

$a) \cos \alpha=\frac{4}{13} ;\left(0<\alpha<\frac{\pi}{2}\right)$

$b) \sin \alpha=-0,7 ;\left(\pi<\alpha<\frac{3 \pi}{2}\right)$

Lời giải

$\text { a) } \cos \alpha=\frac{4}{13}$

- Vận dụng công thức: $\sin ^{2} \alpha+\cos ^{2} \alpha=1$

$\Rightarrow \sin ^{2} \alpha=1-\cos ^{2} \alpha=1-\left(\frac{4}{13}\right)^{2}=1-\frac{16}{169}=\frac{153}{169}$

\(\text { - Vì } 00, \text { nên: }\)

$\Rightarrow \sin \alpha=\sqrt{\frac{153}{169}}=\frac{3 \sqrt{17}}{13}$

$+\tan \alpha=\frac{\sin \alpha}{\cos \alpha}=\frac{3 \sqrt{17}}{13}: \frac{4}{13}=\frac{3 \sqrt{17}}{4}$

$+\cot \alpha=\frac{1}{\tan \alpha}=\frac{4}{3 \sqrt{17}}$

$\text { b) } \sin \alpha=-0,7$

- Vận dụng công thức: $\sin ^{2} \alpha+\cos ^{2} \alpha=1$

$\Rightarrow \cos ^{2} \alpha=1-\sin ^{2} \alpha=1-(-0,7)^{2}=0,51$

- Vì $\pi<\alpha<(3 \pi / 2) \Rightarrow \cos \alpha<0, \text { nên: }$

$\begin{array}{l} \Rightarrow \cos \alpha=-\sqrt{0,51}=-\sqrt{\frac{51}{100}}=-\frac{\sqrt{51}}{10} \\ +\text { tand }=\frac{\sin \alpha}{\cos \alpha}=(-0,7): \frac{-\sqrt{51}}{10}=\frac{7}{\sqrt{51}} \\ +\cot \alpha=\frac{1}{\tan \alpha}=\frac{\sqrt{51}}{7} \end{array}$

Tham khảo thêm : Bài 4 trang 148 SGK Đại Số 10

Ví dụ 2: Tính giá trị lượng giác của góc

$\cos 225^{0} ; \sin 240^{0} ; \cot \left(-15^{0}\right) ; \tan 75^{0}$

Lời giải

Ta có: $225^{\circ}=180^{\circ}+45^{\circ}$

- Nên $\cos 225^{0}=\cos \left(180^{0}+45^{0}\right)=-\cos 45^{0}=\frac{\sqrt{2}}{2}$

+ Có: $240^{\circ}=180^{\circ}+60^{\circ}$

- Nên $\sin 240^{\circ}=\sin \left(180^{0}+60^{0}\right)=-\sin 60^{0}=-\frac{\sqrt{3}}{2}$

+ Có: $\cot \left(-15^{0}\right)=-\cot 15^{0}=-\tan \left(90^{0}-15^{0}\right)$

$\begin{array}{l} =-\tan 75^{0}=-\tan \left(45^{0}+30^{0}\right)=\frac{\tan 45^{0}+\tan 30^{0}}{1-\tan 45^{0} \cdot \tan 30^{0}} \\ =-\frac{1+\frac{\sqrt{3}}{3}}{1-1 \cdot \frac{\sqrt{3}}{3}}=-\frac{3+\sqrt{3}}{3-\sqrt{3}}=-\frac{\sqrt{3}+1}{\sqrt{3}-1}=-(2+\sqrt{3}) \end{array}$

+ Có: $\tan 75^{0}=\tan \left(45^{0}+30^{\circ}\right)=\frac{\tan 45^{0}+\tan 30^{\circ}}{1-\tan 45^{0} \cdot \tan 30^{0}}$

$=\frac{1+\frac{\sqrt{3}}{3}}{1-1 . \frac{\sqrt{3}}{3}}=\frac{3+\sqrt{3}}{3-\sqrt{3}}=\frac{\sqrt{3}+1}{\sqrt{3}-1}=(2+\sqrt{3})$

Dạng 2: Chứng minh đẳng thức lượng giác

Phương pháp giải :

- Để chứng minh đẳng thức lượng giác A = B ta vận dụng các công thức lượng giác và biến đổi vế để đưa A thành A1, A2,... đơn giản hơn và cuối cùng thành B.

- Có bài toán cần sử dụng phép chứng minh tương đương hoặc chứng minh phản chứng.

Ví dụ 1

Chứng minh: $\cos \alpha(1+\cos \alpha)(\tan \alpha-\sin \alpha)=\sin ^{3} \alpha$

Lời giải

- Ta có:

$\begin{array}{l} V T=\cos \alpha(1+\cos \alpha)(\tan \alpha-\sin \alpha) \\ =\cos \alpha(1+\cos \alpha)\left(\frac{\sin \alpha}{\cos \alpha}-\sin \alpha\right) \\ =(1+\cos \alpha)(\sin \alpha-\sin \alpha \cdot \cos \alpha) \\ =\sin \alpha(1+\cos \alpha)(1-\cos \alpha)=\sin \alpha\left(1-\cos ^{2} \alpha\right) \\ =\sin \alpha \cdot \sin ^{2} \alpha=\sin ^{3} \alpha=V P \end{array}$

Ví dụ 2

Chứng minh các đẳng thức: $\frac{\cos (a-b)}{\cos (a+b)}=\frac{\operatorname{cota.cotb}+1}{\operatorname{cota.cotb}-1}$

Lời giải

Ta có:

$V T=\frac{\cos (a-b)}{\cos (a+b)}=\frac{\cos a \cdot \cos b+\sin a \cdot \sin b}{\cos a \cdot \cos b-\sin a \cdot \sin b}$

[Chia cả tử và mẫu cho sina.sinb, ta được]

$\begin{array}{l} =\frac{\frac{\cos a \cdot \cos b+\sin a \cdot \sin b}{\sin a \cdot \sin b}}{\frac{\cos a \cdot \cos b-\sin a \cdot \sin b}{\sin a \cdot \sin b}}=\frac{\frac{\cos a}{\sin a} \cdot \frac{\cos b}{\sin b}+1}{\frac{\cos a}{\sin a} \cdot \cos b-1}{\sin b}-1 \\ =\frac{\operatorname{cota.cotb}+1}{\operatorname{cota.cotb}-1}=V P \end{array}$

- Vậy ta được điều phảo chứng minh.

Dạng 3: Rút gọn một biểu thức lượng giác

Phương pháp giải

- Để rút gọn biểu thức lượng giác chứa góc α ta thực hiện các phép toán tương tự dạng 2 chỉ khác là kết quả bài toán chưa được cho trước.

- Nếu kết quả bài toán sau rút gọn là hằng số thì biểu thức đã cho độc lập với α.

Ví dụ 1

Rút gọn biểu thức: $\sin (a+b)+\sin \left(\frac{\pi}{2}-a\right) \sin (-b)$

Lời giải

Ta có:

$\begin{array}{l} \sin (a+b)+\sin \left(\frac{\pi}{2}-a\right) \sin (-b) \\ =\sin a \cdot \cos b+\cos a \cdot \sin b+\cos a \cdot(-\sin b) \\ =\sin a \cdot \cos b+\cos a \cdot \sin b-\cos a \cdot \sin b=\sin a \cdot \cos b \end{array}$

Ví dụ 2

Rút gọn biểu thức: $A=\frac{\sin x+\sin 3 x+\sin 5 x}{\cos x+\cos 3 x+\cos 5 x}$

Lời giải

- Ta có:$\sin x+\sin 3 x+\sin 5 x$

$\begin{array}{l} =(\sin 5 x+\sin x)+\sin 3 x \\ =2 \sin \left(\frac{5 x+x}{2}\right) \cdot \cos \left(\frac{5 x-x}{2}\right)+\sin 3 x \\ =2 \sin 3 x \cdot \cos 2 x+\sin 3 x \\ =\sin 3 x(2 \cos 2 x+1) \end{array}$

- Tương tự có: $\cos x+\cos 3 x+\cos 5 x$

$\begin{array}{l} =(\cos 5 x+\cos x)+\cos 3 x \\ =2 . \cos \left(\frac{5 x+x}{2}\right) \cdot \cos \left(\frac{5 x-x}{2}\right)+\cos 3 x \\ =2 \cos 3 x \cdot \cos 2 x+\cos 3 x \\ =\cos 3 x(2 \cos 2 x+1) \end{array}$

- Vậy: $A=\frac{\sin x+\sin 3 x+\sin 5 x}{\cos x+\cos 3 x+\cos 5 x}$

$=\frac{\sin 3 x(2 \cos 2 x+1)}{\cos 3 x(2 \cos 2 x+1)}=\frac{\sin 3 x}{\cos 3 x}=\tan 3 x$

Dạng 4: Chứng minh biểu thức độc lập với α

 Phương pháp giải

- Vận dụng các công thức và hiện các phép biến đổi tương tự dạng 3.

Ví dụ 

Chứng minh các biểu thức sau không phụ thuộc $x$

$a) A=\sin \left(\frac{\pi}{4}+x\right)-\cos \left(\frac{\pi}{4}-x\right)$

$b) B=\cos \left(\frac{\pi}{6}-x\right)-\sin \left(\frac{\pi}{3}+x\right)$

Lời giải

a) Ta có: 

$\begin{array}{l} A=\sin \left(\frac{\pi}{4}+x\right)-\cos \left(\frac{\pi}{4}-x\right) \\ =\sin \frac{\pi}{4} \cdot \cos x+\cos \frac{\pi}{4} \cdot \sin x-\left(\cos \frac{\pi}{4} \cdot \cos x+\sin \frac{\pi}{4} \cdot \sin x\right) \\ =\frac{\sqrt{2}}{2} \cos x+\frac{\sqrt{2}}{2} \sin x-\left(\frac{\sqrt{2}}{2} \cos x+\frac{\sqrt{2}}{2} \sin x\right)=0 \end{array}$

⇒ Vậy biểu thức $A=0$ không phụ thuộc vào giá trị của $x$

b) Ta có:

$\begin{array}{l} B=\cos \left(\frac{\pi}{6}-x\right)-\sin \left(\frac{\pi}{3}+x\right) \\ =\cos \frac{\pi}{6} \cdot \cos x+\sin \frac{\pi}{6} \cdot \sin x-\sin \frac{\pi}{3} \cdot \cos x-\cos \frac{\pi}{3} \cdot \sin x \\ =\cos x \cdot\left(\cos \frac{\pi}{6}-\sin \frac{\pi}{3}\right)+\sin x \cdot\left(\sin \frac{\pi}{6}-\cos \frac{\pi}{3}\right) \\ =\cos x .0+\sin x .0=0 \\ \text { (vì } \left.\cos \frac{\pi}{6}=\sin \frac{\pi}{3} ; \sin \frac{\pi}{6}=\cos \frac{\pi}{3}\right) \end{array}$

Dạng 5: Tính giá trị của biểu thức lượng giác

Phương pháp giải:

- Vận dụng công thức và các phép biến đổi như dạng 2 và dạng 3.

Ví dụ

 Tính giá trị của biểu thức: $A=\frac{2 \cos ^{2} \frac{\pi}{8}-1}{1+8 \sin ^{2} \frac{\pi}{8} \cdot \cos ^{2} \frac{\pi}{8}}$

Lời giải

- Vận dụng công thức nhân đôi: $\cos 2 \alpha=2 \cos ^{2} \alpha-1 \text { và } \sin 2 \alpha=2 \sin \alpha \cdot \cos \alpha$

- Ta có: $A=\frac{2 \cos ^{2} \frac{\pi}{8}-1}{1+8 \sin ^{2} \frac{\pi}{8} \cdot \cos ^{2} \frac{\pi}{8}}$
$\begin{array}{l} =\frac{\cos \left(2 \cdot \frac{\pi}{8}\right)}{1+2 \cdot\left(2 \sin \frac{\pi}{8} \cdot \cos \frac{\pi}{8}\right)^{2}}=\frac{\cos \frac{\pi}{4}}{1+2 \sin ^{2} \frac{\pi}{4}} \\ =\frac{\sqrt{2}}{2}:\left[1+2 \cdot\left(\frac{\sqrt{2}}{2}\right)^{2}\right]=\frac{\sqrt{2}}{2}:(1+1)=\frac{\sqrt{2}}{4} \end{array}$

   Như vậy, nội dung bài viết chúng tôi đã tổng hợp toàn bộ các công thức lượng giác toán 10 từ cơ bản tới nâng cao. Bạn chỉ cần nhớ và áp dụng vào giải bài tập là được. Qua bài viết, hy vọng bạn sẽ thích học, đạt những điểm số trong bài thi liên quan đến kiến thức lượng giác và các bài tập môn Toán lớp 10