Câu hỏi
Hình vuông có bao nhiêu trục đối xứng:
A. 2
B. 3
C. 4
D. 0
Đáp án: Hình vuông có 4 trục đối xứng, trong đó:
+ 2 trục đối xứng là hai đường chéo của hình vuông
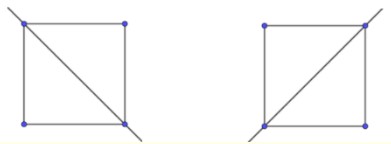
+ 2 trục đối xứng là 2 trục nối trung điểm của hai cạnh đối diện
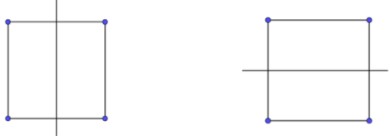
Giải thích
Trục đối xứng là gì?
Đường thẳng d gọi là trục đối xứng của hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua đường thẳng d cũng thuộc hình H. Ta nói hình H có trục đối xứng.
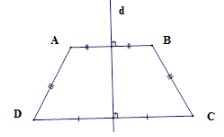
Định lý: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.
Trục đối xứng của một số hình
Đường tròn, trục đối xứng là đường kính của đường tròn. Đường tròn có vô số trục đối xứng.
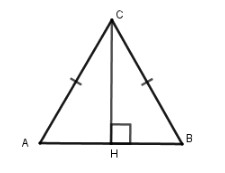
Tam giác cân, trục đối xứng là đường cao, trung trực, trung tuyến, phân giác của tam giác cân xuất phát từ đỉnh ứng với cạnh đáy. Tam giác cân có duy nhất 1 trục đối xứng.
Tam giác đều, trục đối xứng là đường cao, trung trực, trung tuyến, phân giác của tam giác đều. Tam giác đều có 3 trục đối xứng.
Hình thang cân, trục đối xứng là đường thẳng đi qua trung điểm hai đáy của hình thang cân. Hình thang cân có 1 trục đối xứng.
Hình thoi, trục đối xứng là hai đường chéo của hình thoi. Hình thoi có 2 trục đối xứng.
Hình vuông, trục đối xứng là hai đường chéo của hình vuông và hai đường thẳng đi qua trung điểm từng cặp cạnh đối diện của hình vuông. Hình vuông có 4 trục đối xứng.
Hình chữ nhật, trục đối xứng là hai đường thẳng đi qua trung điểm từng cặp cạnh đối diện của hình chữ nhật. Hình chữ nhật có 2 trục đối xứng.
Đa giác đều n cạnh thì có n trục đối xứng
Các dạng toán thường gặp
Dạng 1: Tính độ dài cạnh, chu vi tam giác, tứ giác
Phương pháp:
Sử dụng chú ý: “Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.”
Dạng 2: Chứng minh (nhận biết) các hình đối xứng nhau qua một đường thẳng.
Phương pháp:
Ta sử dụng định nghĩa: “ Hai điểm A,B gọi là đối xứng với nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối hai điểm đó.”