Bài 3 trang 87 sgk toán 7 tập 1 chân trời sáng tạo
Câu hỏi
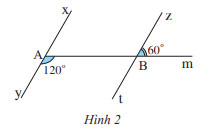
Quan sát Hình 2.
Chứng minh rằng xy // zt
Bài giải
Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {{A_1}} + 120^\circ = 180^\circ \Rightarrow \widehat {{A_1}} = 180^\circ - 120^\circ = 60^\circ \)
Ta có: \(\widehat {{A_1}} = \widehat {{B_1}}( = 60^\circ )\). Mà 2 góc này ở vị trí đồng vị
Nên xy // zt (Dấu hiệu nhận biết 2 đường thẳng song song).
Bài 4 trang 87 sgk toán 7 tập 1 chân trời sáng tạo
Câu hỏi
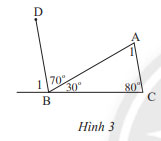
Quan sát Hình 3
a) Tính B1
b) Chứng minh rằng AC // BD
c) Tính A2
Bài giải
a) Vì \(\widehat {{B_1}} + 70^\circ + 30^\circ = 180^\circ \) ( kề bù) nên \(\widehat {{B_1}} = 80^\circ \)
b) Vì \(\widehat {{B_1}} = \widehat {{A_1}}( = 80^\circ )\), mà 2 góc này ở vị trí so le trong nên AC // BD (Dấu hiệu nhận biết 2 đường thẳng song song)
c) Vì AC // BD nên \(\widehat {DBA} = \widehat {{A_1}}\) (2 góc so le trong), mà \(\widehat {DBA} = 70^\circ \Rightarrow \widehat {{A_1}} = 70^\circ \)
Bài 5 trang 87 sgk toán 7 tập 1 chân trời sáng tạo
Câu hỏi
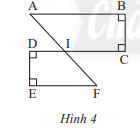
Quan sát Hình 4. Chứng minh rằng:
a) AB // CD và EF // CD
b) AB // EF
Bài giải
a) Vì \(AB \bot BC;CD \bot BC \Rightarrow AB//CD\) ( cùng vuông góc với BC)
Vì \(EF \bot DE;CD \bot DE \Rightarrow EF//CD\)( cùng vuông góc với DE)
b) Vì AB // CD và EF // CD nên AB // EF ( cùng song song với CD)
Bài 6 trang 87 sgk toán 7 tập 1 chân trời sáng tạo
Câu hỏi
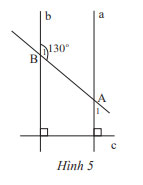
Cho Hình 5 có \(\widehat {{B_1}} = 130^\circ \). Số đo của \(\widehat {{A_1}}\) là bao nhiêu?
Bài giải
Vì a \( \bot \) c, b \( \bot \) c nên a // b ( cùng vuông góc với c)
Ta có: \(\widehat {{B_1}} + \widehat {{B_2}} = 180^\circ \) ( 2 góc kề bù) nên \(130^\circ + \widehat {{B_2}} = 180^\circ \Rightarrow \widehat {{B_2}} = 180^\circ - 130^\circ = 50^\circ \)
Vì a // b nên \(\widehat {{A_1}} = \widehat {{B_2}}\) (2 góc đồng vị) nên \(\widehat {{A_1}} = 50^\circ \)
Bài 7 trang 87 sgk toán 7 tập 1 chân trời sáng tạo
Câu hỏi
Cho Hình 6, biết hai đường thẳng a và b song song với nhau và \(\widehat {{A_1}} = 50^\circ \)
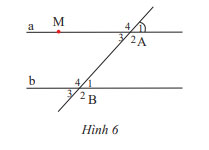
a) Hãy viết tên các cặp góc so le trong và các cặp góc đồng vị.
b) Tính số đo của \(\widehat {{A_3}},\widehat {{B_3}}\)
c) Kẻ đường thẳng c vuông góc với đường thẳng a tại M. Chứng minh rằng c \( \bot \) b.
Bài giải
a) Các cặp góc so le trong là: \(\widehat {{A_3}} = \widehat {{B_1}};\widehat {{A_2}} = \widehat {{B_4}}\)
Các cặp góc đồng vị là : \(\widehat {{A_1}} = \widehat {{B_1}};\widehat {{A_2}} = \widehat {{B_2}};\widehat {{A_3}} = \widehat {{B_3}};\widehat {{A_4}} = \widehat {{B_4}}\)
b) Vì \(\widehat {{A_1}} = \widehat {{A_3}}\) (2 góc đối đỉnh), mà \(\widehat {{A_1}} = 50^\circ \) nên \(\widehat {{A_3}} = 50^\circ \)
Vì a // b nên \(\widehat {{A_3}} = \widehat {{B_3}}\)( 2 góc đồng vị), mà \(\widehat {{A_3}} = 50^\circ \) nên \(\widehat {{B_3}} = 50^\circ \)
c) Gọi c cắt b tại D
Vì a // b nên \(\widehat {{M_1}} = \widehat {{D_1}}\) ( 2 góc so le trong), mà \(\widehat {{M_1}} = 90^\circ \Rightarrow \widehat {{D_1}} = 90^\circ \)
Vậy c \( \bot \) b.
Chú ý: Ta có định lí: Đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì cũng song song vói đường thẳng còn lại
Xem thêm:
- Trang 72 SGK Toán 7 tập 1 Chân trời sáng tạo
- Trang 75 SGK Toán 7 tập 1 Chân trời sáng tạo
- Trang 80 SGK Toán 7 tập 1 Chân trời sáng tạo
- Trang 81 SGK Toán 7 tập 1 Chân trời sáng tạo
- Trang 84 SGK Toán 7 tập 1 Chân trời sáng tạo
- Trang 86 SGK Toán 7 tập 1 Chân trời sáng tạo
Trên đây là chi tiết hướng dẫn Giải bài tập Trang 87 SGK Toán 7 tập 1 Chân trời sáng tạo được Đọc Tài Liệu biên soạn với mong muốn hỗ trợ các em học sinh học tốt hơn môn Toán lớp 7
Hướng dẫn giải Toán 7 Chân trời sáng tạo bởi Đọc Tài Liệu