Bài 9.26 trang 81 sgk toán 7 tập 2 Kết nối tri thức
Câu hỏi
Gọi H là trực tâm của tam giác ABC không vuông. Tìm trực tâm của các tam giác HBC, HCA, HAB.
Bài giải
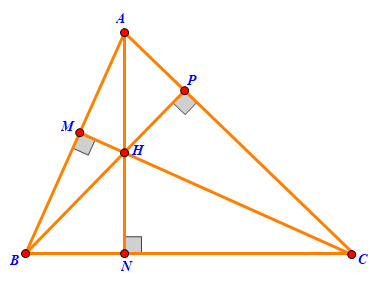
a)
Trong ΔABC ta có H là trực tâm nên:
AH ⊥ BC tại N, BH ⊥ AC tại P, CH ⊥ AB tại M
Trong ΔAHB, ta có:
HM ⊥ AB
BN ⊥ AH
Mà MH cắt BN tại C
=> C là trực tâm của tam giác AHB.
Trong ΔHAC, ta có:
HP ⊥ AC
CN ⊥ AH
Mà HP cắt CN tại B
=> B là trực tâm của ΔHAC.
Trong ΔHBC, ta có:
HN ⊥ BC
BM ⊥ HC
Mà HN cắt BM tại A
=> A là trực tâm của tam giác HBC
Bài 9.27 trang 81 sgk toán 7 tập 2 Kết nối tri thức
Câu hỏi
Cho tam giác ABC có \(\widehat A = {100^0}\) và trực tâm H. Tìm góc BHC.
Bài giải
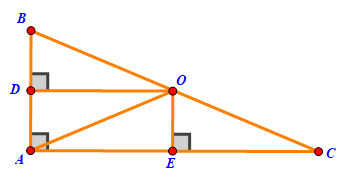
Gọi E là chân đường cao từ C xuống AB, D là chân đường cao từ B xuống AC
=> HC ⊥ BE, HB ⊥ CD
Ta có:
\(\begin{array}{l}\widehat {BAC} + \widehat {BAD} = {180^0}\\ \Rightarrow {100^0} + \widehat {BAD} = {180^0}\\ \Rightarrow \widehat {BAD} = {180^0} - {100^0}\\ \Rightarrow \widehat {BAD} = {80^0}\end{array}\)
∆ ADB là tam giác vuông tại D:
\(\begin{array}{l}\widehat {BAD} + \widehat {ABD} = {90^0}\\ \Rightarrow {80^0} + \widehat {ABD} = {90^0}\\ \Rightarrow \widehat {ABD} = {10^0}\end{array}\)
∆ BEH là tam giác vuông tại E
\(\begin{array}{l}\widehat {EBH} + \widehat {BHE} = {90^0}\\ \Rightarrow {10^0} + \widehat {BHE} = {90^0}\\ \Rightarrow \widehat {BHE} = {80^0}\end{array}\)
Hay \(\widehat {BHC} = {80^0}\)
Bài 9.28 trang 81 sgk toán 7 tập 2 Kết nối tri thức
Câu hỏi
Xét điểm O cách đều 3 đỉnh của tam giác ABC. Chứng minh rằng nếu O nằm trên một cạnh của tam giác ABC thì ABC là một tam giác vuông.
Bài giải
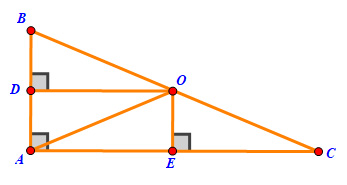
O cách đều 3 đỉnh của tam giác ABC
\( \Rightarrow \) \(OA = OB = OC\)
\( \Rightarrow \) \(\Delta OAB\) cân tại O.
Giả sử O là trung điểm BC
\( \Rightarrow \widehat {OAB} = \widehat {OBA}\)
\(\Delta OAC\) cân tại O
\( \Rightarrow \widehat {OAC} = \widehat {OCA}\)
Xét tam giác ABC có
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^0}\\ \Rightarrow \widehat A + \widehat {OAB} + \widehat {OAC} = {180^0}\\ \Rightarrow \widehat A + \widehat A = {180^0}\\ \Rightarrow \widehat A = {90^0}\end{array}\)
Vậy nếu O nằm trên một cạnh của tam giác ABC thì ABC là một tam giác vuông.
Bài 9.29 trang 81 sgk toán 7 tập 2 Kết nối tri thức
Câu hỏi
a) Có một chi tiết máy ( đường viền ngoài là đường tròn) bị gãy. (H.9.46). Làm thế nào để xác định được bán kính của đường viền này ?
b) Trên bản đồ, ba khu dân cư được quy hoạch tại điểm A, B, C không thẳng hàng. Hãy tìm trên bản đồ một điểm M cách đều A, B, C để quy hoạch một trường học
Bài giải
a)
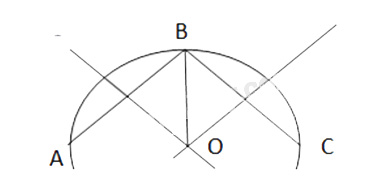
- Lấy ba điểm phân biệt A, B, C trên đường viền ngoài chi tiết máy.
- Vẽ đường trung trực cạnh AB và cạnh BC. Hai đường trung trực này cắt nhau tại O. Khi đó O là tâm cần xác định.
- Bán kính đường tròn cần tìm là độ dài đoạn OB (hoặc OA hoặc OC).
b)
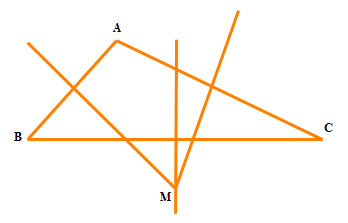
- Bước 1: Vẽ đường trung trực của các đoạn AB, AC, BC
- Bước 2: 3 đường trung trực này cắt nhau tại M. Khi đó MA= MB=MC.
- Bước 3: M là điểm cần xác định.
Bài 9.30 trang 81 sgk toán 7 tập 2 Kết nối tri thức
Câu hỏi
Cho hai đường thẳng không vuông góc b,c cắt nhau tại điểm A và cho điểm H không thuộc b và c (H.9.47). Hãy tìm điểm B thuộc b, điểm C thuộc c sao cho tam giác ABC nhận H làm trực tâm.
Bài giải
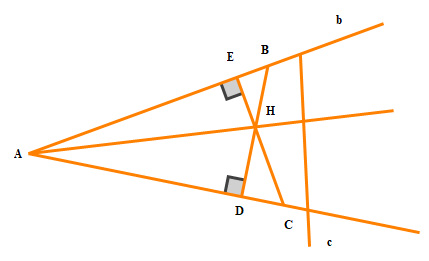
- Kẻ HD \( \bot \) đường thẳng c tại điểm D, HE \( \bot \) đường thẳng b tại điểm E
- Nối A với H. Kéo dài DH cắt đường thẳng b tại B.
Từ B kẻ đường vuông góc với AH, đường thẳng đó cắt đường thẳng c tại 1 điểm. Điểm đó chính là điểm C.
=> H là trực tâm của tam giác ABC.
Bài tiếp theo: Trang 83 SGK Toán 7 tập 2 Kết nối tri thức
Xem thêm:
- Trang 62 SGK Toán 7 tập 2 Kết nối tri thức
- Trang 65 SGK Toán 7 tập 2 Kết nối tri thức
- Trang 69 SGK Toán 7 tập 2 Kết nối tri thức
- Trang 71 SGK Toán 7 tập 2 Kết nối tri thức
- Trang 76 SGK Toán 7 tập 2 Kết nối tri thức
- Trang 84 SGK Toán 7 tập 2 Kết nối tri thức
Trên đây là chi tiết hướng dẫn Giải bài tập Trang 81 SGK Toán 7 tập 2 Kết nối tri thức được Đọc Tài Liệu biên soạn với mong muốn hỗ trợ các em học sinh học tốt hơn môn Toán lớp 7
Hướng dẫn giải Toán 7 Kết nối tri thức bởi Đọc Tài Liệu