Bài 3.9 trang 43 sgk toán 10 tập 1 Kết nối tri thức
Câu hỏi
Trên nóc một tòa nhà có một cột ăng-ten cao 5m. Từ một vị trí quan sát A cao 7 m so với mặt đất có thể nhìn thấy đỉnh B và chân C của cột ăng-ten, với các góc tương ứng là \({50^o}\)và \({40^o}\) so với phương nằm ngang (H.3.18).
a) Tính các góc của tam giác ABC.
b) Tính chiều cao của tòa nhà.
Bài giải
a)
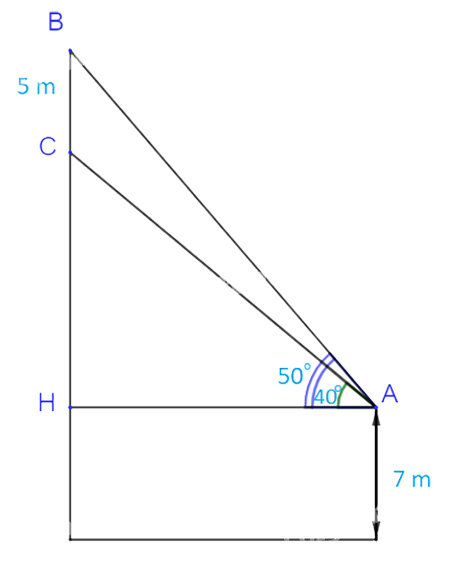
Gọi H là hình chiếu của A lên đường thẳng BC.
Ta có: \(\widehat {HAB} = {50^o}\); \(\widehat {HAC} = {40^o}\)
\( \Rightarrow \widehat {BAC} = {50^o} - {40^o} = {10^o}\) (1)
Xét tam giác ABH, vuông tại H ta có:
\(\widehat H = {90^o};\;\widehat {BAH} = {50^o}.\)
\( \Rightarrow \widehat {HBA} = {180^o} - {90^o} - {50^o} = {40^o}\) hay \(\widehat {CBA} = {40^o}\). (2)
Từ (1) và (2), suy ra: \(\widehat {BCA} = {180^o} - {40^o} - {10^o} = {130^o}.\)
Vậy ba góc của tam giác ABC lần lượt là: \(\widehat A = {10^o};\;\widehat B = {40^o};\;\widehat C = {130^o}\).
b)
Áp dụng định lý sin cho tam giác ABC, ta được:
\(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\) \( \Rightarrow AB = \frac{{BC.\sin C}}{{\sin A}}\)
Mà: \(BC = 5\;(m);\;\;\widehat C = {130^o};\;\widehat A = {10^o}\)
\( \Rightarrow AB = \frac{{5.\sin {{130}^o}}}{{\sin {{10}^o}}} \approx 22\;(m)\)
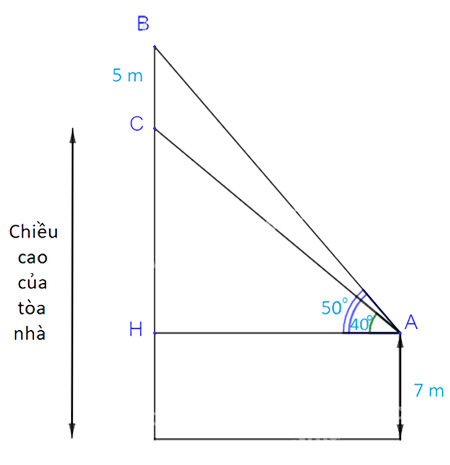
Xét tam giác ABH, vuông tại H ta có:
\(\sin \widehat {BAH} = \frac{{BH}}{{AB}}\)\( \Rightarrow BH = AB.\,\,\sin \widehat {BAH}\)
Mà: \(AB \approx 22\;(m);\;\;\widehat {BAH} = {50^o}\)
\( \Rightarrow BH \approx 22.\sin {50^o} \approx 16,85\;(m)\)
Vậy chiều cao của tòa nhà là: \(BH-{\rm{ }}BC + 7 = 16,85-5 + 7 = 18,85{\rm{ }}\left( m \right)\)
Bài 3.10 trang 43 sgk toán 10 tập 1 Kết nối tri thức
Câu hỏi
Từ bãi biển Vũng Chùa, Quảng Bình, ta có thể ngắm được Đảo Yến. Hãy đề xuất một các xác định bề rộng của hòn đảo (theo chiều ta ngắm được).
Bài giải
Bước 1:
Đánh dấu vị trí quan sát tại điểm A, chiều rộng của hòn đảo kí hiệu là đoạn BC.
Gọi H là hình chiếu của A trên BC.
Trên tia đối của tia AH, lấy điểm M, ghi lại khoảng cách AM = a.
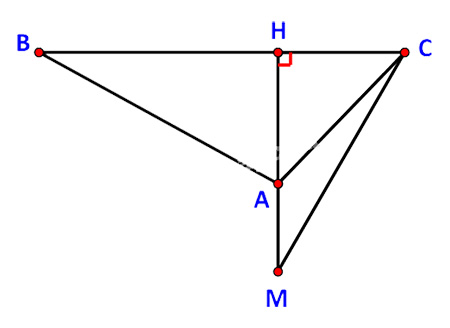
Bước 2:
Tại A, quan sát để xác định các góc \(\widehat {BAC} = \alpha ,\;\widehat {HAC} = \beta \).
Tiếp tục quan sát tại M, xác định góc \(\widehat {HMC} = \gamma \).
Bước 3: Giải tam giác AMC, tính AC.
AM = a, \(\widehat {AMC} = \widehat {HMC} = \gamma \) và \(\widehat {MAC} = {180^o} - \beta \)
\( \Rightarrow \widehat {ACM} = {180^o} - \gamma - \left( {{{180}^o} - \beta } \right) = \beta - \gamma \)
Áp dụng định định lí sin trong tam giác AMC ta có:
\(\frac{{AC}}{{\sin AMC}} = \frac{{AM}}{{\sin ACM}} \Rightarrow AC = \sin \gamma .\frac{a}{{\sin \left( {\beta - \gamma } \right)}}\)
Bước 4:
\(\widehat {ABC} = {90^o} - \widehat {HAB} = {90^o} - (\alpha - \beta )\)
Áp dụng định lí sin cho tam giác ABC ta có:
\(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} \Rightarrow BC = \sin \alpha .\frac{{\sin \gamma .\frac{a}{{\sin \left( {\beta - \gamma } \right)}}}}{{\sin \left( {{{90}^o} - (\alpha - \beta )} \right)}}.\).
Bài 3.11 trang 43 sgk toán 10 tập 1 Kết nối tri thức
Câu hỏi
Để tránh núi, giao thông hiện tại phải đi vòng như mô hình trong Hình 3.19. Để rút ngắn khoảng cách và tránh sạt lở núi, người ta dự định làm đường hầm xuyên núi, nối thẳng từ A tới D. Hỏi độ dài đường mới sẽ giảm bao nhiêu kilômét so với đường cũ?
Bài giải
Bước 1:
Áp dụng định lí cos trong tam giác ABC ta có:
\(\begin{array}{l}A{C^2} = {6^2} + {8^2} - 2.6.8.\cos {105^o}\\ \Rightarrow AC \approx 11,17\;(km)\end{array}\)
Bước 2:
Lại có: Theo định lí sin thì
\(\begin{array}{l}\frac{{AB}}{{\sin ACB}} = \frac{{AC}}{{\sin ABC}} \Rightarrow \sin ACB = \frac{{8.\sin {{105}^o}}}{{11,17}}\\ \Rightarrow \widehat {ACB} \approx 43,{77^o}\\ \Rightarrow \widehat {ACD} = {135^o} - 43,{77^o} = 91,{23^o}\end{array}\)
Bước 3:
Áp dụng định lí cos trong tam giác ACD ta có:
\(\begin{array}{l}A{D^2} = {12^2} + 11,{17^2} - 2.12.11,17\cos 91,{23^o}\\ \Rightarrow AD \approx 16,57\;(km)\end{array}\)
Bước 4:
Độ dài đường mới giảm số kilomet so với đường cũ là: \(12 + 6 + 8 - 16,57 = 9,43\;(km)\)
Bài tiếp theo: Trang 44 SGK Toán 10 tập 1 Kết nối tri thức
Xem thêm:
- Trang 37 SGK Toán 10 tập 1 Kết nối tri thức
- Trang 42 SGK Toán 10 tập 1 Kết nối tri thức
- Trang 45 SGK Toán 10 tập 1 Kết nối tri thức
Trên đây là chi tiết hướng dẫn Giải bài tập Trang 43 SGK Toán 10 tập 1 Kết nối tri thức được Đọc Tài Liệu biên soạn với mong muốn hỗ trợ các em học sinh học tốt hơn môn Toán lớp 10
Hướng dẫn giải Toán 10 Kết nối tri thức bởi Đọc Tài Liệu