Có $F_{\mathrm{d} h} \max =k \cdot\left(\Delta l_{0}+A\right)>F_{k v} \max =k . A$
$\rightarrow$ đường cao hơn là $\mathrm{F}_{{đh }}$, đường thấp hơn là $\mathrm{F}_{\mathrm{kv}}$.
Lập ti số: $\frac{F_{\text {dh }} m a x}{F_{k v} \max }=\frac{\Delta l_{0}+A}{A}=\frac{3}{2} \rightarrow \Delta l_{0}=\frac{A}{2}$
Tại $\mathrm{t}_{1}$ thì $\mathrm{F}_{\mathrm{d} \mathrm{h}}=0$ và $\mathrm{F}_{\mathrm{dl}}$ đang tăng
=> vật qua vị tri tự nhiên $\left(x=-\frac{A}{2}\right)$ theo chiều durơng Đến $\mathrm{t}_{2}$ thì $\mathrm{F}_{\mathrm{kv}}=0$ và $\mathrm{F}_{\mathrm{kv}}=0$ lần thứ $2 \mathrm{kề}$ tù $\mathrm{t}_{1} \rightarrow$ vật qua vị trí cân bằng theo chiều âm
$\rightarrow t_{2}-t_{1}=\frac{7 \pi}{120}=\frac{T}{12}+\frac{T}{2}=\frac{7 T}{12}=\frac{7 \pi}{120}(\mathrm{~s})$
$\rightarrow \mathrm{T}=0,1 \pi(\mathrm{s}) \rightarrow \omega=\frac{2 \pi}{T}=20(\mathrm{rad} / \mathrm{s})$
Có $ \Delta l_{0}=\frac{g}{\omega^{2}}=\frac{10}{20^{2}}=0,025(\mathrm{~m})=2,5 \mathrm{~cm} $
$\rightarrow \mathrm{A}=2 \Delta l_{0}=5(\mathrm{~cm})$ vị trí lò xo dãn } $6,5 \mathrm{~cm}$ có li độ $\mathrm{x}=6,5-2,5=4(\mathrm{~cm}) $
=> tốc độ $\mathrm{v}=\omega \sqrt{A^{2}-x^{2}}=20 \cdot \sqrt{5^{2}-4^{2}}=60(\mathrm{~cm} / \mathrm{s})$
Một con lắc lò xo treo thẳng đứng, dao động điều hòa tại nơi có g=10 m / s2.
Xuất bản: 01/04/2021 - Cập nhật: 01/04/2021 - Tác giả: Chu Huyền
Câu Hỏi:
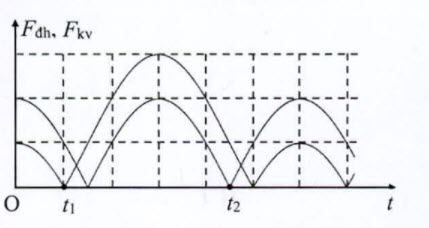
Một con lắc lò xo treo thẳng đứng, dao động điều hòa tại nơi có $g=10 {~m} / {s}^{2}$. Hinh bên là đồ thị biểu diễn sự phụ thuộc của độ lớn lực kéo về $F_{{kv}}$ tác dụng lên vật và độ lớn lực đàn hồi $F_{\text {db }}$ của lò xo theo thời gian $t$. Biết $t_{2}-t_{1}=\frac{7 \pi}{120}$ (s). Khi lò xo dãn $6,5 {~cm}$ thì tốc độ của vật là

Câu hỏi trong đề: Đề minh họa tốt nghiệp THPT 2021 môn Lý có đáp án chi tiết từng câu
Đáp án và lời giải
đáp án đúng: B
