Một cái ly có dạng hình nón như sau Người ta đổ một lượng nước vào ly sao cho

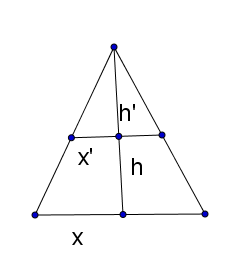
Minh họa trước và sau khi úp ly như hình vẽ.
Thể tích phần nước ${V_n} = \frac{1}{3}\left( {\pi x{'^2}} \right).h' = \frac{1}{3}\pi {\left( {\frac{x}{2}} \right)^2}.\left( {\frac{h}{2}} \right) = \frac{1}{3}.\frac{1}{8}.\pi {x^2}h.$
Vậy thể tích phần không có nước ${V_t} = \frac{1}{3}\pi {x^2}h - \frac{1}{3}.\frac{1}{8}\pi {x^2}h = \frac{1}{3}.\frac{7}{8}\pi {x^2}h$ hay $\frac{1}{3}.\pi x'{'^2}h'' = \frac{1}{3}.\frac{7}{8}\pi {x^2}h$.
Mặt khác $\frac{{x''}}{x} = \frac{{h''}}{h} \Rightarrow {\left( {\frac{{h''}}{h}} \right)^3} = \frac{7}{8} \Rightarrow \frac{{h''}}{h} = \frac{{\sqrt[3]{7}}}{2} \Rightarrow h'' = \frac{{\sqrt[3]{7}h}}{2}.$
Vậy chiều cao của nước và chiều cao của ly
$\frac{{h - h''}}{h} = \frac{{h - \frac{{\sqrt[3]{7}h}}{2}}}{h} = \frac{{2 - \sqrt[3]{7}}}{2}.$