Có bao nhiêu giá trị nguyên âm của tham số m để hàm số y=x3+m x-frac15 x5 đồng

$y^{\prime}=3 x^{2}+m+\frac{1}{x^{6}}$

Hàm số đồng biến trên $(0 ;+\infty)$ khi và chỉ khi $y^{\prime}=3 x^{2}+m+\frac{1}{x^{6}} \geq 0, \forall x \in(0 ;+\infty)$

$\Leftrightarrow-3 x^{2}-\frac{1}{x^{6}} \leq m, \forall x \in(0 ;+\infty)$. Xét hàm số $g(x)=-3 x^{2}-\frac{1}{x^{6}} \leq m, x \in(0 ;+\infty)$

$g^{\prime}(x)=-6 x+\frac{6}{x^{7}}=\frac{-6\left(x^{8}-1\right)}{x^{7}}, g^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{l}x=1 \\ x=-1(\text { loai })\end{array}\right.$

Bảng biến thiên: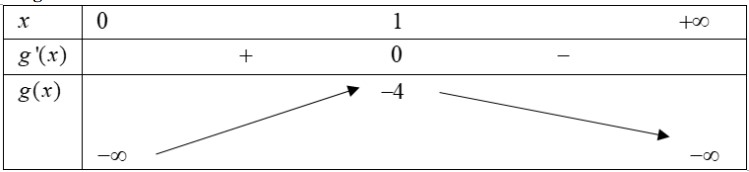



Dựa vào BBT ta có $m \geq-4$ , suy ra các giá trị nguyên âm của tham số $m$ là $-4 ;-3 ;-2 ;-1$